黑龙江省哈尔滨市第三中学校2024-2025学年高二上学期期中考试数学

这是一份黑龙江省哈尔滨市第三中学校2024-2025学年高二上学期期中考试数学，文件包含黑龙江省哈尔滨市第三中学校2024-2025学年高二上学期期中考试数学docx、黑龙江省哈尔滨市第三中学校2024-2025学年高二上学期期中考试数学pdf等2份试卷配套教学资源，其中试卷共42页， 欢迎下载使用。

高二学年期中考试
数学试卷
考试说明：
（1）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分.考试时间为120分钟；
（2）第Ⅰ卷，第Ⅱ卷试题答案均答在答题卡上，交卷时只交答题卡.
第Ⅰ卷（选择题，共58分）
一、选择题（共58分）
（一）单项选择题（共8小题，每小题5分.在每小题给出的四个选项中，只有一项是符合题目要求的）
1．圆的圆心和半径分别是（ ）
A．，2B．，2
C．，D．，
2．下列命题是真命题的是（ ）
A．经验回归方程至少经过其样本数据点，，…，中的一个
B．可以用相关系数r来刻画两个变量x和y线性相关程度的强弱，r的绝对值越小，说明两个变量线性相关程度越强
C．线性回归分析中决定系数用来刻画回归的效果，若值越小，则模型的拟合效果越好
D．残差点分布在以横轴为对称轴的水平带状区域内，该区域越窄，拟合效果越好
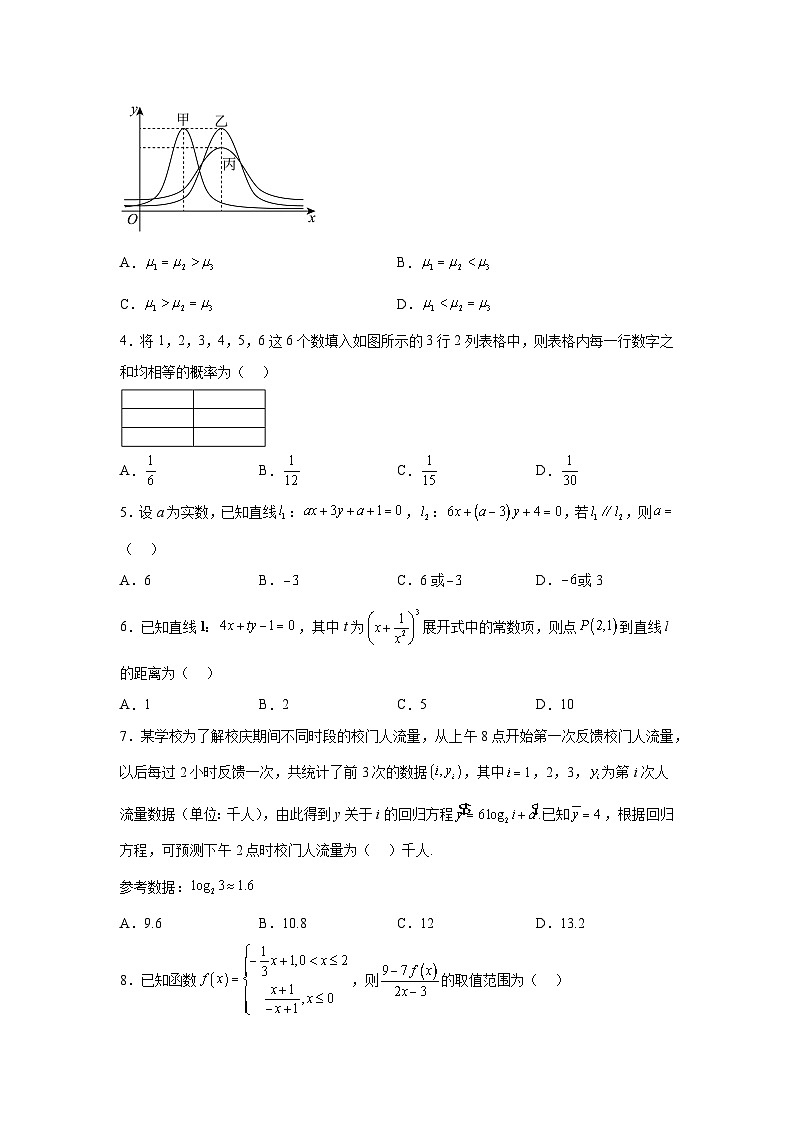
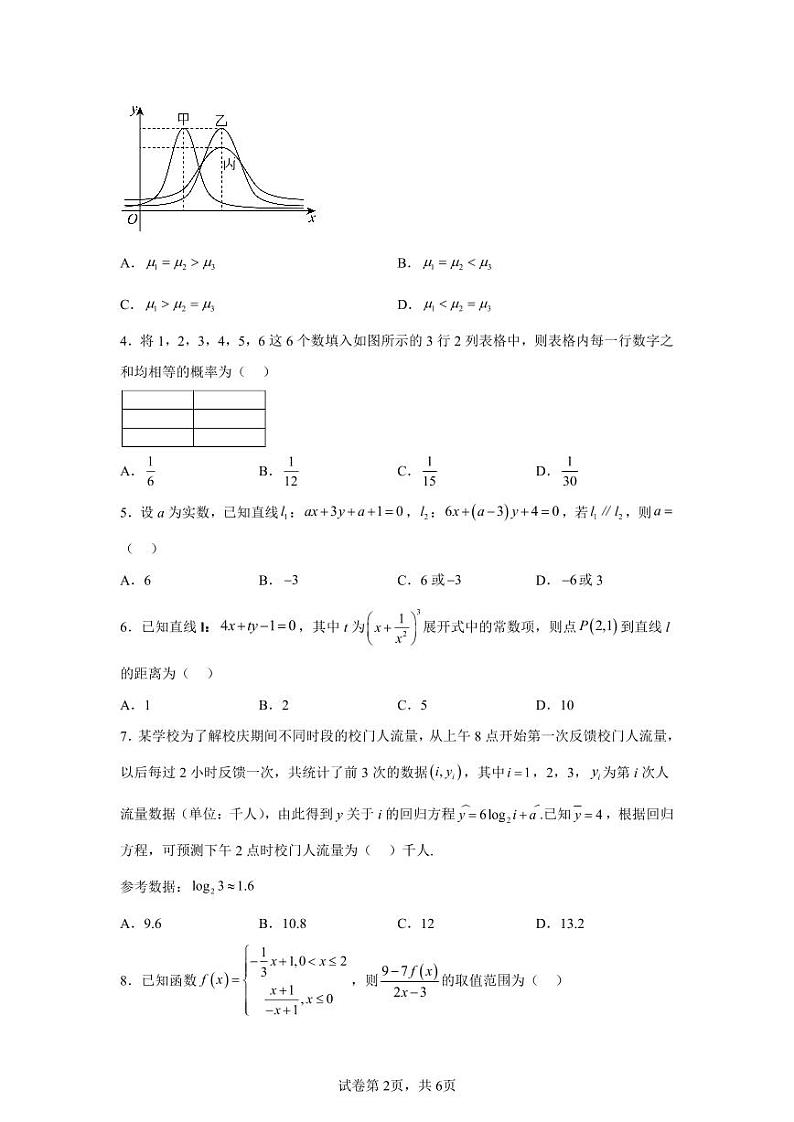
3．某市高中数学统考中，甲、乙、丙三所学校的数学成绩分别服从正态分布，，，其正态分布的密度曲线如图所示，则（ ）
A．B．
C．D．
4．将1，2，3，4，5，6这6个数填入如图所示的3行2列表格中，则表格内每一行数字之和均相等的概率为（ ）
A．B．C．D．
5．设a为实数，已知直线：，：，若，则（ ）
A．6B．C．6或D．或3
6．已知直线l：，其中t为展开式中的常数项，则点到直线l的距离为（ ）
A．1B．2C．5D．10
7．某学校为了解校庆期间不同时段的校门人流量，从上午8点开始第一次反馈校门人流量，以后每过2小时反馈一次，共统计了前3次的数据，其中，2，3，为第i次人流量数据（单位：千人），由此得到y关于i的回归方程.已知，根据回归方程，可预测下午2点时校门人流量为（ ）千人.
参考数据：
A．9.6B．10.8C．12D．13.2
8．已知函数，则的取值范围为（ ）
A．B．
C．D．
（二）多项选择题（共3小题，每小题6分.在每小题给出的选项中，有多项符合题目要求，全部选对的得6分，部分选对的得部分分，有选错的得0分）
9．关于函数，下列命题中正确的是（ ）
A．是以为最小正周期的周期函数
B．的最大值为
C．将函数的图象向左平移个单位后，与已知函数的图象重合
D．的图象关于直线对称
10．在平面直角坐标系中，定义为两点Ax1,y1，Bx2,y2的“切比雪夫距离”，又设点及直线上任意一点，称的最小值为点到直线的“切比雪夫距离”，记作，则下列命题中正确的是（ ）
A．，，则
B．为坐标原点，动点满足，则的轨迹为圆
C．对任意三点、、，都有
D．已知点和直线：，则
11．高考数学试题第二部分为多选题，共个小题，每小题有个选项，其中有个或个是正确选项，全部选对得分，部分选对得部分分，有选错的得分.若正确答案是个选项，只选对个得分，有选错的得分；若正确答案是个选项，只选对个得分，只选对个得分，有选错的得分.小明对其中的一道题完全不会，该题有两个正确选项的概率是，记为小明随机选择个选项的得分，记为小明随机选择个选项的得分，则（ ）
A．B．
C．D．
第Ⅱ卷（非选择题，共92分）
二、填空题（本大题共3小题，每小题5分，共15分.将答案填在答题卡相应的位置上）
12．下列说法中正确的有 （填正确说法的序号）
①直线的倾斜角为
②直线的斜率为
③直线（）过定点
④点到直线的距离为1
13．对于随机事件，若，，，则 .
14．已知正方体的棱长为2，E、F为空间内两点且，，.当三棱锥的体积最大时，其外接球的表面积为 .
三、解答题（本大题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤）
15．的内角A，B，C的对边分别为a，b，c，已知
(1)求锐角的大小；
(2)在（1）的条件下，若，且的周长为，求的面积.
16．已知的三个顶点分别是，，
(1)求边AC的高BH所在直线方程；
(2)已知M为AB中点，试在直线CM上求一点P，在x轴上求一点Q，使的周长最小，并求最小值.
17．随着冬天的临近，哈尔滨这座冰雪之城，将再次成为旅游的热门目的地.为更好地提升旅游品质，我市文旅局随机选择名青年游客对哈尔滨出行体验进行满意度评分（满分分），分及以上为良好等级，根据评分，制成如图所示的频率分布直方图.
(1)根据频率分布直方图，求x的值并估计该评分的上四分位数；
(2)若采用按比例分层抽样的方法从评分在，的两组中共抽取6人，再从这6人中随机抽取4人进行单独交流，求选取的4人中评分等级为良好的人数X的分布列和数学期望；
(3)为进一步了解不同年龄段游客对哈尔滨出行体验的反馈，我市文旅局再次随机选择100名中老年游客进行满意度评分，发现两次调查中评分为良好等级的人数为120名.请根据小概率值的独立性检验，分析游客的评分等级是否良好与年龄段（青年或中老年）是否有关.
附：，
18．棱长为2的正方体，M为正方体中心，将四棱锥绕逆时针旋转（）后得到四棱锥，如图1.

(1)求四棱锥的表面积和体积；
(2)若（如图2），求证：平面平面；
(3)求为多少时，直线与直线DC所成角最小，并求出最小角的余弦值.
19．某志愿者社团计划在周一和周二两天各举行一次活动，分别由甲、乙两人负责活动通知，已知该社团共有n位同学，每次活动均需k位同学参加.假设甲和乙分别将各自活动通知的信息独立、随机地发给该社团k位同学，且所发信息都能收到.
(1)当，时，求该社团只有小明同学同时收到甲、乙两人所发活动通知信息的概率；
(2)记至少收到一个活动通知信息的同学人数为X
①设，，求随机变量X的分布列和数学期望；
②求使取得最大值的整数m.
0.05
0.01
0.001
3.841
6.635
10.828
1．C
【分析】由圆的标准方程直接可得出圆的圆心和半径.
【详解】圆的圆心为，半径为.
故选：C.
2．D
【分析】根据经验回归方程、相关系数、决定系数、残差等知识确定正确答案.
【详解】对于A，经验回归方程是由最小二乘法计算出来的，它不一定经过其样本数据点，一定经过，所以A错误；
对于B，由相关系数的意义，当越接近1时，表示变量y与x之间的线性相关程度越强，所以B错误；
对于C，用决定系数的值判断模型的拟合效果，越大，模型的拟合效果越好，所以C是错误；
对于D，因为在残差的散点图中，残差分布的水平带状区域的宽度越窄，表明数据越集中，
模型的拟合效果越好，故D正确.
故选：D.
3．D
【分析】根据给定的曲线，利用正态分布的密度曲线的特征判断即得.
【详解】观察曲线知，.
故选：D
4．C
【分析】根据题意，先将6个数字分为3组，再将三组全排列，安排在表格的三行中，由分步计数原理计算计算个数，即可由古典概型概率公式求解.
【详解】要使表格内每一行数字之和均相等，根据，
先将6个数字分为3组，分别为，，；
将三组全排列，安排在表格的三行中，每一行有种顺序，
则可组成不同表格的个数为；
将1，2，3，4，5，6这6个数填入表格中的所有情况,
故概率为
故选：C．
5．A
【分析】由题可得，据此可得的可能值，验证后可得答案.
【详解】因，则.
则或.当，：，：，满足；
当，：，：，两直线重合，不合题意.
则.
故选：A
6．B
【分析】根据二项式展开式的通项特征可得，即可根据点到直线的距离公式求解.
【详解】展开式的常数项为,故，
所以直线l：，
故点到直线l的距离为，
故选：B
7．B
【分析】令，由，求出，得回归方程，可求预测值.
【详解】令，则，
，又，
由，得，所以，
则，
下午2点时对应，可得.
故选：B.
8．B
【分析】化简，函数上一点与连线斜率的倍，求出的范围，即可得出答案.
【详解】因为，图象如下图，，
，
表示函数上一点与连线斜率的倍，
，，，
由图可知：或，
所以或，
则的取值范围为.
故选：B.
9．ABD
【分析】根据辅助角公式可得，即可根据周期以及最值求解AB，根据平移的性质即可判断C，代入验证即可求解D.
【详解】,
对于A，最小正周期为，A正确，
对于B，由于的最大值为1，故的最大值为，B正确，
对于C，的图象向左平移个单位后，得到，故C错误，
对于D，，故的图象关于直线对称，D正确，
故选：ABD
10．ACD
【分析】对于A：根据切比雪夫距离的定义直接运算即可；
对于B：设，分析可得，且等号至少有一个成立，即可得结果；
对于C：根据题意结合绝对值不等式的分析判断；
对于D：设点可得，讨论可得距离，再由函数的性质，求得最小值.
【详解】对于选项A：若，，则，
因为，所以，故A正确；
对于选项B：设，
若，则，且等号至少有一个成立，
可得的轨迹如图所示，为正方形，故B错误；
对于选项C：设，
则
，
同理可得，
所以，故C正确；
对于选项D：设为直线上一点，
则，
当，即时，则，
可知当时，取得最小值；
当，即或，则，无最小值；
综上可得：，故D正确；
故选：ACD.
【点睛】方法点睛：“新定义”主要是指即时定义新概念、新公式、新定理、新法则、新运算五种，然后根据此新定义去解决问题，有时还需要用类比的方法去理解新的定义，这样有助于对新定义的透彻理解.对于此题中的新概念，对阅读理解能力有一定的要求.但是，透过现象看本质，它们考查的还是基础数学知识，所以说“新题”不一定是“难题”，掌握好三基，以不变应万变才是制胜法宝.
11．BCD
【分析】分别计算出和的分布列，然后逐项进行计算即可求得.
【详解】由题意，，若该题有两个正确选项，则小明从两个错误选项中选择个；若该题有个正确选项，则小明从个错误选项中选择个，
概率为：；
，该题有个正确选项，则小明从个正确选项中选择个，
概率为：；
，该题有个正确选项，则小明从个正确选项中选择个，
概率为：；
，若该题有两个正确选项，则小明从两个错误选项中选择个或选择个错误选项；若该题有个正确选项，则小明从个错误选项中选择个，再从个正确选项中选一个，概率为：；
，该题有个正确选项，则小明从个正确选项中选择个，
概率为：；
，该题有个正确选项，则小明从个正确选项中选择个，
概率为：；
对于A选项，， A错误；
对于B选项，；
；所以， B正确；
对于C选项，，
，C正确；
对于D选项，，D正确.
故选：BCD.
12．①③
【分析】对于①，根据斜率与倾斜角的关系可判断，对于②，将直线化为一般式，即可判断；对于③，将直线化为，故可判断；对于④，根据点到直线的距离公式即可判断.
【详解】对于①，直线的斜率为，
根据倾斜角满足，即，故①正确；
对于②，将直线化为一般式为，
所以斜率为，故②错误；
对于③，将直线化为，
所以时，，不论取值，故直线过定点，故③正确；
对于④，根据点到直线的距离公式，故④错误.
故答案为：①③
13．
【分析】根据条件概率公式及概率的性质计算即可.
【详解】因为，所以，
则，
所以，
又，
所以，解得.
故答案为：.
14．
【分析】根据条件得到为中点，在平面内，其中为定值，只需点到平面的距离最大，建立空间直角坐标系，设，，得到平面的法向量，利用点到平面距离的向量公式得到当时，点到平面的距离最大，此时与重合，求出⊥平面，设球心，由得到方程组，求出球心和半径，求出表面积.
【详解】因为，所以为中点，
又，，故在平面内，
其中为定值，只需点到平面的距离最大，
以为坐标原点，所在直线分别为轴，建立空间直角坐标系，
正方体的棱长为2，
故，设，，
设平面的法向量为，
则，
令得，故，
则到平面的距离，
故当时，点到平面的距离最大，此时，即与重合，
设球心，由得
，
解得，
故外接球球心为，半径为，
故外接球表面积为.

故答案为：
【点睛】方法点睛：几何体外接球问题，通常要找到几何体的一个特殊平面，利用正弦定理，几何性质找到其外心，求出外接圆的半径，进而找到球心的位置，进而求出半径，也可以利用空间向量的方放，设出球心坐标，待定系数法进行求解
15．(1)
(2)
【分析】（1）利用正弦定理化边为角，再结合两角和的正弦公式即可得解；
（2）先求出，再根据正弦定理，令，求出，再根据三角形的周长求出，再根据三角形的面积公式即可得解.
【详解】（1）因为，
由正弦定理得，
即，
又，所以，
又，所以；
（2）因为，所以，
又，所以，
则，
由正弦定理，令，
则，
所以的周长为，
解得，
所以，
所以.
16．(1)
(2)当时，的周长最小，最小值为.
【分析】（1）求出边AC的高BH的斜率，再由点斜式方程即可得出答案.
（2）先求出直线CM的方程，如图，作出关于直线CM的对称点，作出关于轴的对称点，则连结，交直线CM于，交轴于，则的周长的最小值等于，最后求出直线的方程，即可求出点Q.
【详解】（1）因为，，所以，
所以边AC的高BH的斜率为，又因为直线BH过点，
所以BH所在直线方程为：，
化简可得：.
所以BH所在直线方程为.
（2）因为M为AB中点，所以，，
直线CM的方程为：，化简可得：，
如图，作出关于直线的对称点，
则，解得：，所以，
作出关于轴的对称点，
连结，交直线CM于，交轴于，
，，
三角形的周长为线段的长，
由两点间线段最短得此时的周长最小，
的周长最小时，最小值为：，
此时直线的斜率为，
直线的方程为：，化简可得：，
令，所以，所以，
所以当时，的周长最小，最小值为.
17．(1)，
(2)分布列见解析，
(3)无法认为游客的评分等级是否良好与年龄段有关.
【分析】（1）根据频率和为计算出的值；先判断出上四分位数所在区间，然后结合区间端点值以及该组的频率完成计算；
（2）先根据分层抽样计算出每组抽取的人数，然后确定出的可取值并计算对应概率，由此可求分布列和数学期望；
（3）根据已知条件得到对应列联表，然后计算出的值并与对应比较大小，由此得到结论.
【详解】（1）由频率分布直方图可知，，解得；
因为的频率为，且为最后一组，
所以评分的上四分位数位于区间中，
所以上四分位数为：；
（2）评分在与两组的频率分别为，
所以内抽取人数为，内抽取人数为，
故人中评分等级为良好的有人，
由题意可知，的可取值为，
，，，
所以的分布列为：
数学期望；
（3）青年游客评分等级良好的有人，所以老年游客评分等级良好的有人，
由上可得如下列联表，
零假设：游客的评分等级是否良好与年龄段无关，
由表中数据可得，
根据小概率值的独立性检验，可知零假设成立，
即无法认为游客的评分等级是否良好与年龄段有关.
18．(1)表面积为，体积为
(2)证明见解析
(3)时，直线与直线DC所成角最小，最小角的余弦值为
【分析】（1）根据棱锥的表面积公式和体积公式计算即可；
（2）易得平面､平面为同一个平面，补全正方体，证明为二面角的平面角，再证明即可；
（3）以为原点，建立空间直角坐标系，利用向量法求解即可.
【详解】（1）由题意，，
则，
所以四棱锥的表面积为，
四棱锥的高为，
则；
（2）若，则平面､平面为同一个平面，
如图，补全正方体，
连接、，则是中点，是中点，

所以平面与平面重合，平面与平面重合，
由正方体性质可知平面，
因为平面，所以，，
为二面角的平面角，
因为，则，同理可得，
所以，所以平面平面；
（3）如图，以为原点，建立空间直角坐标系，

则，
，即，
故，
则，
因为，所以，
所以，
所以，
所以，此时，即，
所以时，直线与直线DC所成角最小，最小角的余弦值为.
【点睛】方法点睛：证明面面垂直常用的方法：
（1）面面垂直的定义；
（2）面面垂直的判定定理.
在证明面面垂直时，一般假设面面垂直成立，然后利用面面垂直转化为线面垂直，即为所证的线面垂直，组织论据证明即可.
19．(1)；
(2)①分布列见解析，数学期望为；②答案见解析.
【分析】（1）根据给定条件，利用古典概率，结合事件的独立性及组合计数问题列式求解.
（2）①求出的可能取值及对应的概率，列出分布列并求出期望；②按和分类求出的表达式，再建立不等式求出对应的整数.
【详解】（1）设事件“该社团只有小明同学同时收到甲、乙两人所发活动通知信息”，
所以.
（2）①的可能取值为2，3，4，
，
所以的分布列为：
数学期望.
②当时，只能取，此时有；
当时，整数满足，其中是和中的较小者，
由甲和乙各自独立、随机地发送活动信息给k位同学，得所包含的基本事件总数为，
当时，同时收到甲乙两人所发信息的学生人数为，
仅收到李老师或张老师转发信息的学生人数为，
由分步乘法原理知，事件所包含的基本事件数为，
，
当时，，
，
因此取得最大值时，满足，
假如成立，则当能被整除时，在和处达到最大；
当不能被整除时，在处达到最大值（表示不超过的最大整数），
下面证明：
由，得，
，则，显然，
因此.
【点睛】关键点点睛：求使取得最大值的值，关键是求出的表达式，再利用最大概率问题求解.
青年游客
老年游客
总计
评分等级良好
评分等级非良好
总计
2
3
4