

2024-2025学年上海市崇明中学高二(上)期中数学试卷(含解析)
展开
这是一份2024-2025学年上海市崇明中学高二(上)期中数学试卷(含解析),共21页。试卷主要包含了填空题,选择题,解答题等内容,欢迎下载使用。
1.(4分)夹在两个平行平面间的两个几何体,如果被平行于这两个平面的任意平面截得的两个截面都有相等的面积,那么这两个几何体的体积,的关系是 .
2.(4分)若平面与平面平行,且,,则直线与直线的位置关系是 .
3.(4分)在空间直角坐标系中,点,6,关于平面对称点的坐标是 .
4.(4分)已知空间两个角与,若,,,则 .
5.(4分)四面体的所有棱长均为2,则二面角的大小为 .
6.(4分)已知、分别是平面、的法向量,且,则 .
7.(5分)母线长为10的圆锥的侧面展开图的圆心角等于,则该圆锥的体积为 .
8.(5分)如图,一个封闭的三棱柱容器中盛有水,侧棱,若当侧面水平放置时,液面恰好经过,,,的中点,则当底面水平放置时,液面的高度为 .
9.(5分)如图,一个水平放置的平面图形的斜二测直观图是直角梯形,其中,,,,则平面图形的面积为 .
10.(5分)设直线与平面所成角为,给出下列命题:(1)平面上不存在直线,使之与所成角小于;(2)设,平面上恰有两条直线与所成角均为;(3)若直线,则直线与所成角大小为;其中真命题的序号为 .
11.(5分)如图,正方形中,,分别是,的中点,沿,,把这个正方形折成一个四面体,使,,三点重合,重合后的点记为.若四面体外接球的表面积为,则正方形的边长为 .
12.(5分)从正方体八个顶点的两两连线中任取两条直线,,且,是异面直线,则,所成角的余弦值的所有可能取值构成的集合是 .
二、选择题(13-14题,每题4分:15-16题,每题5分,总计18分)
13.(4分)当我们停放自行车时,只要将自行车的撑脚放下,自行车就稳了,这用到了
A.三点确定一个平面
B.不在同一直线上的三点确定一个平面
C.两条相交直线确定一个平面
D.两条平行直线确定一个平面
14.(4分)关于直线,及平面,,下列命题中正确的是
A.若,,则B.若,,则
C.若,,则D.若,,则
15.(5分)正方体中,与的交点称为正方体的中心,平面经过点,且顶点,到平面的距离相等,则这样的平面的个数为
A.1B.2C.0D.无数个
16.(5分)如图,正方体的棱长为1,、分别是棱、的中点,经过直线的平面分别与棱、交于点、,设,,给出下列三个结论:
①四边形一定是菱形;
②若四边形的面积为,,则有最大值与最小值;
③若四棱锥的体积为,,则为常值函数.
以上结论中,正确结论的个数是
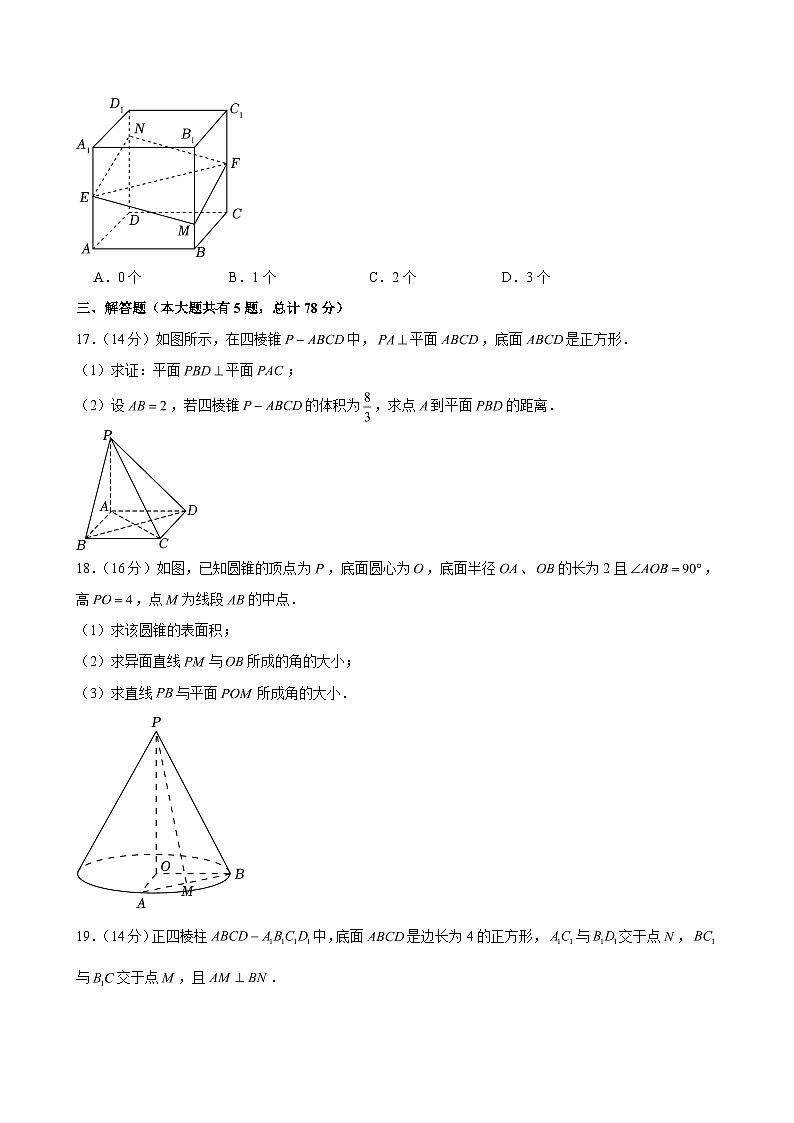
A.0个B.1个C.2个D.3个
三、解答题(本大题共有5题,总计78分)
17.(14分)如图所示,在四棱锥中,平面,底面是正方形.
(1)求证:平面平面;
(2)设,若四棱锥的体积为,求点到平面的距离.
18.(16分)如图,已知圆锥的顶点为,底面圆心为,底面半径、的长为2且,高,点为线段的中点.
(1)求该圆锥的表面积;
(2)求异面直线与所成的角的大小;
(3)求直线与平面所成角的大小.
19.(14分)正四棱柱中,底面是边长为4的正方形,与交于点,与交于点,且.
(1)用向量方法求的长;
(2)对于个向量,如果存在不全为零的个实数,,,,使得,则称个向量叫做线性相关,否则称为线性无关.试判断是否线性相关.
20.(16分)如图所示,在正方体中,、分别是、的中点.求证:
(1)四边形是梯形;
(2)、、三线共点;
(3)直线和直线是异面直线.
21.(18分)已知点是边长为2的菱形所在平面外一点,且点在底面上的射影是与的交点,已知,是等边三角形.
(1)求证:;
(2)求点到平面的距离;
(3)若点是线段上的动点,问:点在何处时,直线与平面所成的角最大?求出最大角,并说明点此时所在的位置.
参考答案
一、填空题(1-6题,每题4分;7-12题,每题5分,总计54分)
1.(4分)夹在两个平行平面间的两个几何体,如果被平行于这两个平面的任意平面截得的两个截面都有相等的面积,那么这两个几何体的体积,的关系是 相等 .
解:根据祖暅原理可得:
夹在两个平行平面间的两个几何体,如果被平行于这两个平面的任意平面截得的两个截面都有相等的面积,那么这两个几何体的体积相等.
故答案为:相等.
2.(4分)若平面与平面平行,且,,则直线与直线的位置关系是 平行或异面 .
解:因为平面平面,可得两平面,无公共点,
又,,
所以直线与直线也无公共点,
所以直线与直线可能平行或异面.
故答案为:平行或异面.
3.(4分)在空间直角坐标系中,点,6,关于平面对称点的坐标是 ,6, .
解:点,6,关于平面对称点的坐标是,6,.
故答案为:,6,.
4.(4分)已知空间两个角与,若,,,则 或 .
解:因为,,
由等角定理可得:
或.
故答案为:或.
5.(4分)四面体的所有棱长均为2,则二面角的大小为 .
解:将正四面体放到棱长为的正方体中,如图所示,
以为原点,建立空间直角坐标系,
则,0,,,,,
所以,,,,
设平面的法向量为,则,
令,则,所以,
设平面的法向量为,则,
令,则,所以,
所以,,
由图可知,二面角为锐二面角,
所以二面角的大小为.
故答案为:.
6.(4分)已知、分别是平面、的法向量,且,则 .
解:根据题意,若,则有,
设,即,1,,,,,,
则有,
即,
所以.
故答案为:.
7.(5分)母线长为10的圆锥的侧面展开图的圆心角等于,则该圆锥的体积为 .
解:因为母线长为10的圆锥的侧面展开图的圆心角等于,
所以侧面展开图的弧长为:,
设该圆锥的底面圆的半径为,
所以,解得,
所以该圆锥的高,
所以该圆锥的体积.
故答案为:.
8.(5分)如图,一个封闭的三棱柱容器中盛有水,侧棱,若当侧面水平放置时,液面恰好经过,,,的中点,则当底面水平放置时,液面的高度为 6 .
解:不妨令此三棱柱为直三棱柱,如图
当侧面水平放置时,水的形状为四棱柱形,底面是梯形.
设的面积为,则,
.
当底面水平放置时,水的形状为三棱柱形,设水面高为,则有,
,.
故当底面水平放置时,液面高为6.
故答案为:6
9.(5分)如图,一个水平放置的平面图形的斜二测直观图是直角梯形,其中,,,,则平面图形的面积为 .
解:在直角梯形中,,,,
显然,于是,
直角梯形对应的原平面图形为如图中直角梯形,
,,,,
所以该平面图形的高为,
故平面图形的面积为:.
故答案为:.
10.(5分)设直线与平面所成角为,给出下列命题:(1)平面上不存在直线,使之与所成角小于;(2)设,平面上恰有两条直线与所成角均为;(3)若直线,则直线与所成角大小为;其中真命题的序号为 (1)(3) .
解:对于(1),如图,为直线与平面所成角,
设是平面内任意一条直线,,
,
结合线面角的范围可得,故(1)正确;
对于(2),若平面上有一条直线与所成角均为,则此平面内与该直线平行的直线都与所成角均为,因此(2)错误;
对于(3),如图,
若直线,则直线与所成角大小为,故(3)正确.
故答案为:(1)(3).
11.(5分)如图,正方形中,,分别是,的中点,沿,,把这个正方形折成一个四面体,使,,三点重合,重合后的点记为.若四面体外接球的表面积为,则正方形的边长为 .
解:依题意,折叠后的四面体如图1所示:
设正方形边长为,外接球半径为,则,解得;
则四面体中,底面,且,,,
把四面体补充成长方体,如图2所示:
则四面体的外接球也是长方体的外接球,所以,
,
所以.
故答案为:.
12.(5分)从正方体八个顶点的两两连线中任取两条直线,,且,是异面直线,则,所成角的余弦值的所有可能取值构成的集合是 .
解:因为正方体八个顶点的两两连线中任取两条直线,,且,是异面直线,
又异面直线的夹角范围为,所以其余弦值范围为,,
可以分为以下几类:
两条棱所在直线异面时,所成角的度数是,其余弦值为0;
面对角线与棱所在直线异面时,所成角的度数是或,其余弦值为或0;
两条面对角线异面时,所成角的度数是或,其余弦值为或0;
体对角线与棱所在直线异面时,所成角的余弦值为;
体对角线与面对角线异面时,所成角的度数是,其余弦值为0;
所以从正方体八个顶点的两两连线中任取两条直线,,且,是异面直线,则,所成角的余弦值的所有可能取值构成的集合是.
故答案为:.
二、选择题(13-14题,每题4分:15-16题,每题5分,总计18分)
13.(4分)当我们停放自行车时,只要将自行车的撑脚放下,自行车就稳了,这用到了
A.三点确定一个平面
B.不在同一直线上的三点确定一个平面
C.两条相交直线确定一个平面
D.两条平行直线确定一个平面
解:自行车前后轮与撑脚分别接触地面,此时三个接触点不在同一条线上,
所以可以确定一个平面,即地面,从而使得自行车稳定.
故选:.
14.(4分)关于直线,及平面,,下列命题中正确的是
A.若,,则B.若,,则
C.若,,则D.若,,则
解:由直线,及平面,,知:
在中,若,,则与平行或异面,故错误;
在中,若,,则与相交、平行或异面,故错误;
在中,若,,则由线面垂直的性质定理得,故正确;
在中,若,,则与相交、平行或,故错误.
故选:.
15.(5分)正方体中,与的交点称为正方体的中心,平面经过点,且顶点,到平面的距离相等,则这样的平面的个数为
A.1B.2C.0D.无数个
解:取中点,连接,则过的任何平面,顶点,到平面的距离相等,
故选:.
16.(5分)如图,正方体的棱长为1,、分别是棱、的中点,经过直线的平面分别与棱、交于点、,设,,给出下列三个结论:
①四边形一定是菱形;
②若四边形的面积为,,则有最大值与最小值;
③若四棱锥的体积为,,则为常值函数.
以上结论中,正确结论的个数是
A.0个B.1个C.2个D.3个
解:对于①,如图,连接,,,,
因为平面平面,平面平面,
平面平面,
所以,同理可得,
所以四边形为平行四边形,
因为平面,平面,所以,
又因为,,平面,,
所以平面,又平面,所以,
因为,分别是,的中点,
所以,且,
所以四边形为平行四边形,所以,
所以,所以四边形为菱形,故①正确;
对于②,由题意得,,,
在矩形中,可得,
四边形的面积,
,则当时,有最小值1,
没有最大值,故②错误;
对于③,如图,连接,,,,,,
四棱锥被分割为三棱锥与三棱锥,
因为平面,平面,所以,
又,,平面,,
所以平面,
所以,点到平面的距离等于,
即点到平面的距离等于,
因为,平面,平面,
所以平面,又,
故点到平面的距离等于点到平面的距离,为,
同理,点到平面的距离也为,
而,
四棱锥的体积
,
则为常值函数,故③正确.
故选:.
三、解答题(本大题共有5题,总计78分)
17.(14分)如图所示,在四棱锥中,平面,底面是正方形.
(1)求证:平面平面;
(2)设,若四棱锥的体积为,求点到平面的距离.
【解答】(1)证明:因为底面是正方形,
所以,
又平面,且平面,
所以,
因为,、平面,
所以平面,
又平面,
所以平面平面.
(2)解:因为四棱锥的体积为,
所以,即,
所以,
由勾股定理知,,
所以是等边三角形,其面积为,
设点到平面的距离为,
因为,
所以,即,
所以点到平面的距离为.
18.(16分)如图,已知圆锥的顶点为,底面圆心为,底面半径、的长为2且,高,点为线段的中点.
(1)求该圆锥的表面积;
(2)求异面直线与所成的角的大小;
(3)求直线与平面所成角的大小.
解:(1)面圆半径为2,,
故母线长,
.
(2)底面,底面,
,
又,即,,,平面,
平面,
取中点,连接,则,且,
为异面直线与所成的角,
由平面,,可得平面,平面,
得,
在△中,求得,
在△中,可得,
所以异面直线与所成的角的大小为.
(3)底面,底面,
,又,是中点,
故,,,平面,
平面,
故即为直线与平面所成角,
由于,,
故,
因此.
19.(14分)正四棱柱中,底面是边长为4的正方形,与交于点,与交于点,且.
(1)用向量方法求的长;
(2)对于个向量,如果存在不全为零的个实数,,,,使得,则称个向量叫做线性相关,否则称为线性无关.试判断是否线性相关.
解:(1)设长为,以为坐标原点,所在直线分别为轴、轴、轴,建立如图所示空间直角坐标系,则,0,,,4,,,
,
由,故,即有,
解得(负值舍去),即;
(2)由,故,
设实数,,,使得成立.
则有,解得时,即当且仅当时
线性无关.
20.(16分)如图所示,在正方体中,、分别是、的中点.求证:
(1)四边形是梯形;
(2)、、三线共点;
(3)直线和直线是异面直线.
【解答】证明:(1)在正方体中,、分别是、的中点,如下图:
连接,所以,且,
故,由于与不平行,
故四边形是梯形;
(2)分别延长,,交于点,,面,
面.
是的中点,,
是的中点,
连接,,
,的交点为线段的中点,即为,
,,三线共点于.
(3)假如直线和直线不是异面直线,则存在一个平面,使得,,
由于在正方体中,,,
因此,
又因为平面,且平面,
故,在正方形中,显然,不平行,故矛盾,
因此假设不成立,即直线和直线是异面直线.
21.(18分)已知点是边长为2的菱形所在平面外一点,且点在底面上的射影是与的交点,已知,是等边三角形.
(1)求证:;
(2)求点到平面的距离;
(3)若点是线段上的动点,问:点在何处时,直线与平面所成的角最大?求出最大角,并说明点此时所在的位置.
【解答】证明:(1)因为点在底面上的射影是与的交点,所以平面,
因为平面,所以,
因为四边形为菱形,所以,
因为,,平面,
所以平面,
因为平面,所以;
解:(2)由题意可得、与都是边长为2的等边三角形,
所以,
所以,
因为,所以,
设点到平面的距离为,
由得,
即,解得,
故点到平面的距离为;
(3)设直线与平面所成的角为,平面,
到平面的距离即为到平面的距离,
过作垂线平面交于点,则,
此时,要使最大,则需使最小,此时,
经计算得,,则,
此时在线段上靠近点的处.
相关试卷
这是一份2024-2025学年上海市浦东新区洋泾中学高三(上)期中数学试卷(含解析),共17页。试卷主要包含了填空题,选择题,解答题等内容,欢迎下载使用。
这是一份2024-2025学年上海市崇明中学高二(上)期中数学试卷(含解析),共20页。
这是一份上海市崇明中学2024-2025学年高二上学期期中考试数学试卷(无答案),共4页。试卷主要包含了填空题,选择题,解答题等内容,欢迎下载使用。









