浙江省温州市瑞安市部分学校2024-2025学年上学期九年级数学期中试卷

这是一份浙江省温州市瑞安市部分学校2024-2025学年上学期九年级数学期中试卷，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题：本题共10小题，每小题3分，共30分。在每小题给出的选项中，只有一项是符合题目要求的。
1.下列事件是必然事件的是( )
A. 明天早上会下雨B. 掷一枚硬币，正面朝上
C. 任意一个三角形，它的内角和等于180∘D. 一个图形旋转后所得的图形与原图形不全等
2.已知⊙O的半径为5，点P到圆心O的距离为4.5，则点P在( )
A. 圆外B. 圆上C. 圆内D. 不能确定
3.不透明的袋子中装有1个红球，3个绿球，这些球除颜色外无其他差别，从中随机摸出一个球，恰好是红球的概率是( )
A. 14B. 13C. 12D. 34
4.下列图形中，既是轴对称图形，又是中心对称图形的是( )
A. 正三角形B. 正五边形C. 正六边形D. 正七边形
5.如图，两条直线AC和DF被三条平行线所截，交点分别为A、B、C和D、E、F，若AB：BC=2：3，DE=3，则EF的长为( )
A. 4.5B. 5C. 6D. 8
6.为了解学生在假期中的阅读量，语文老师统计了全班学生在假期里的看书数量，统计结果如表：那么假期里该班学生看书数量的平均数与众数分别为( )
A. 4，5B. 5，4C. 4，4D. 5，5
7.下列命题正确的是( )
A. 平分弦所对的两条弧的直线必垂直于弦B. 垂直于弦的直线平分弦
C. 平分弦的直线必平分弦所对的两条弧D. 平分弦的直径必平分弦所对的两条弧
8.如图，线段AB是半圆O的直径．分别以点A和点O为圆心，大于12AO的长为半径作弧，两弧交于M，N两点，作直线MN，交半圆O于点C，交AB于点E，连接AC，BC，若AE=1，则BC的长是( )
A. 2 3
B. 4
C. 6
D. 3 2
9.若点m,n在抛物线y=ax2a>0上，其中m>0，则不等式ax-22>n的解为( )
A. x<-m+2或x>m+2B. -m+2C. x<-m-2或x>m-2D. -m-210.已知二次函数y=x2-4x+3的图象经过点P，点P的横坐标为m，当m≤x≤4时，总有-1≤y≤4m，则m的值为( )
A. 4+ 13B. 4- 13C. 4± 13D. 34
二、填空题：本题共6小题，每小题3分，共18分。
11.下表是某种植物的种子在相同条件下发芽率试验的结果．
根据上表中的数据，可估计该植物的种子发芽的概率为 (精确到0.01)．
12.如图，▵AOB绕点O逆时针旋转62∘得到△COD，若∠COD=29∘，则∠BOC= 度．
13.已知线段a=2，b=8，则a，b的比例中项线段长是 ．
14.将抛物线y=(x-1)2-3先向左平移2个单位，再向下平移1个单位，得到的新抛物线解析式是 ．
15.已知⊙O的直径AB=10cm，CD是⊙O的弦，AE⊥CD，垂足为点E，BF⊥CD，垂足为点F，且CD=8cm，则BF-AE的长为______cm．
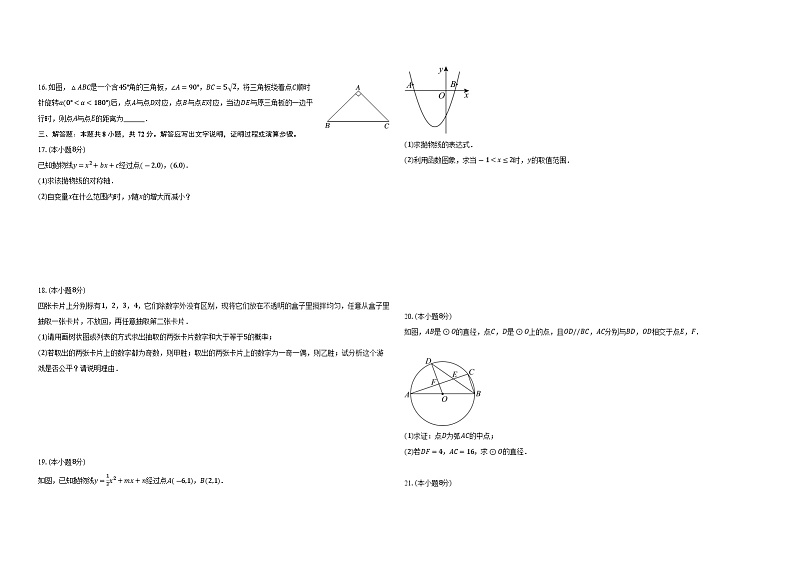
16.如图，△ABC是一个含45°角的三角板，∠A=90°，BC=5 2，将三角板绕着点C顺时针旋转α(0°<α<180°)后，点A与点D对应，点B与点E对应，当边DE与原三角板的一边平行时，则点A与点E的距离为______．
三、解答题：本题共8小题，共72分。解答应写出文字说明，证明过程或演算步骤。
17.(本小题8分)
已知抛物线y=x2+bx+c经过点(-2,0)，(6,0)．
(1)求该抛物线的对称轴．
(2)自变量x在什么范围内时，y随x的增大而减小？
18.(本小题8分)
四张卡片上分别标有1，2，3，4，它们除数字外没有区别，现将它们放在不透明的盒子里搅拌均匀，任意从盒子里抽取一张卡片，不放回，再任意抽取第二张卡片．
(1)请用画树状图或列表的方式求出抽取的两张卡片数字和大于等于5的概率；
(2)若取出的两张卡片上的数字都为奇数，则甲胜；取出的两张卡片上的数字为一奇一偶，则乙胜；试分析这个游戏是否公平？请说明理由．
19.(本小题8分)
如图，已知抛物线y=12x2+mx+n经过点A-6,1，B(2,1)．
(1)求抛物线的表达式．
(2)利用函数图象，求当-120.(本小题8分)
如图，AB是⊙O的直径，点C，D是⊙O上的点，且OD//BC，AC分别与BD，OD相交于点E，F．
(1)求证：点D为弧AC的中点；
(2)若DF=4，AC=16，求⊙O的直径．
21.(本小题8分)
某商店购进一种商品，每件商品进价20元，规定该商品的售价不低于进价，且不高于进价的两倍．试销中发现这种商品每天的销售量y(件)与每件销售价x(元)的关系数据如下：
(1)已知y与x满足一次函数关系，根据上表，求出y与x之间的关系式；
(2)设该商店每天销售这种商品所获利润为w(元)，求出每件商品销售价定为多少元时利润最大，并求出最大利润？
22.(本小题10分)
如图，一小球从斜坡O点以一定的方向弹出球的飞行路线可以用二次函数y=ax2+bx(a<0)刻画，斜坡可以用一次函数y=0.25x刻画，小球飞行的水平距离x(米)与小球飞行的高度y(米)的变化规律如下表：
(1) ①m=，n=；②小球的落点是A，求点A的坐标．
(2)小球飞行高度y(米)与飞行时间t(秒)满足关系y=-5t2+vt，求v的值．
23.(本小题10分)
如图，有一座拱桥是圆弧形，它的跨度AB=60米，拱高PD=18米，
(1)求圆弧所在的圆的半径r的长；
(2)当洪水泛滥到跨度只有30米时，要采取紧急措施，若拱顶离水面只有4米，即PE=4米是否要采取紧急措施？
24.(本小题12分)
在平面直角坐标系中，抛物线y=-x2-4x+c与x轴交于点A，B(点A在点B的左侧)，与y轴交于点C，且点A的坐标为(-5,0)．
(1)求点C的坐标；
(2)如图1，若点P是第二象限内抛物线上一动点，求点P到直线AC距离的最大值；
(3)如图2，若点M是抛物线上一点，点N是抛物线对称轴上一点，是否存在点M使以A，C，M，N为顶点的四边形是平行四边形？若存在，请直接写出点M的坐标；若不存在，请说明理由．
答案和解析
1.【答案】C
【解析】本题考查了必然事件、不可能事件、随机事件的概念．用到的知识点为：必然事件指在一定条件下，一定发生的事件；不可能事件是指在一定条件下，一定不发生的事件；不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件．
直接利用随机事件以及必然事件的定义分析得出答案．
【详解】解：A、明天早上会下雨，是随机事件，故此选项不符合题意；
B、掷一枚硬币，正面朝上，是随机事件，故此选项不符合题意；
C、任意一个三角形，它的内角和等于180∘，是必然事件，故此选项符合题意；
D、一个图形旋转后所得的图形与原图形不全等，是不可能事件，故此选项不符合题意；
故选：C．
2.【答案】C
【解析】本题考查了点与圆的位置关系．熟练掌握：点P在圆外⇔d>r；点P在圆上⇔d=r；点P在圆内⇔d【详解】解：由题意知，r=5,d=4.5，
∴d故选：C．
3.【答案】A
【解析】直接由概率公式求解即可．
【详解】解：∵袋子中装有1个红球，3个绿球，每个球被摸到的概率相同，
∴从不透明的袋子中随机摸出一个球，恰好是红球的概率是11+3=14，
故选：A．
4.【答案】C
【解析】根据轴对称图形与中心对称图形的概念求解即可．
【详解】A、此图形不是中心对称图形，是轴对称图形，故此选项错误；
B、此图形不是中心对称图形，是轴对称图形，故此选项错误；
C、此图形既是中心对称图形，又是轴对称图形，故此选项正确；
D、此图形不是中心对称图形，是轴对称图形，故此选项错误．
故选：C．
5.【答案】A
【解析】解：∵两条直线AC和DF被三条平行线所截，
∴EFDE=BCAB，
又∵AB：BC=2：3，DE=3，
∴EF3=32，
∴EF=4.5．
故选：A．
由两条直线AC和DF被三条平行线所截，利用平行线分线段成比例定理，可得出EFDE=BCAB，再结合AB：BC=2：3，DE=3，即可求出EF的长．
本题考查了平行线分线段成比例，牢记“三条平行线截两条直线，所得的对应线段成比例”是解题的关键．
6.【答案】C
【解析】解：由题意可知，假期里该班学生看书数量的平均数=2×6+3×6+4×10+5×8+6×56+6+10+8+5=4(本)，
∵看书数量为4本的有10人，人数最多，
∴众数为4(本)，
故选：C．
直接根据平均数及众数的定义求解即可．
本题考查了众数和加权平均数，解题的关键是熟练掌握平均数的计算公式．
7.【答案】A
【解析】解：A、平分弦所对的两条弧的直线必垂直于弦，符合题意；
B、垂直于弦的直径平分弦，故原说法错误，不符合题意；
C、平分弦的直径必平分弦所对的两条弧，故原说法错误，不符合题意；
D、平分弦(不是直径)的直径必平分弦所对的两条弧，故原说法错误，不符合题意；
故选：A．
根据垂径定理和垂径定理的推论进行判断即可．
本题考查了命题与定理，垂径定理，熟练掌握垂径定理及其推论是解决问题的关键．
8.【答案】A
【解析】解：如图，连接OC．
根据作图知CE垂直平分AO，
∴AC=OC，AE=OE=1，
∴OC=OB=AO=AE+EO=2，
∴AC=OC=AO=AE+EO=2，
即AB=AO+BO=4，
∵线段AB是半圆O的直径，
∴∠ACB=90°，
在Rt△ACB中，根据勾股定理得，BC= AB2-AC2= 42-22=2 3，
故选A．
根据作图知CE垂直平分AO，即可得AC=OC，AE=OE=1，根据圆的半径得AC=2，AB=4，根据圆周角定理的推论得∠ACB=90°，根据勾股定理即可得BC= AB2-AC2=2 3．
本题考查了作图-基本作图，圆，勾股定理，圆周角定理的推论，线段垂直平分线的性质，解题的关键是掌握这些知识点．
9.【答案】A
【解析】本题考查了二次函数的性质，以及解不等式，先由点m,n在抛物线y=ax2a>0上得n=am2，再将其代入不等式ax-22>n，再根据a>0，m>0得出解集即可．
【详解】解：∵点m,n在抛物线y=ax2a>0上，
∴n=am2，
∵ax-22>n，
∴ax-22>am2，
∵a>0，
∴x-22>m2，
又∵m>0，
∴x-2<-m或x-2>m，
∴x<-m+2或x>m+2，
故选：A．
10.【答案】D
【解析】本题考查二次函数的图象及性质．
将二次函数的解析式配方成顶点式，可得出抛物线的开口向上，顶点坐标为2,-1，对称轴是直线x=2，当x=2时，y取得最小值-1，由已知“当m≤x≤4时，总有-1≤y≤4m”根据抛物线的对称性和增减性分类讨论∶若0【详解】解：∵y=x2-4x+3=x-22-1，
a=1>0，
∴抛物线的开口向上，顶点坐标为2,-1，对称轴是直线x=2，
∴当x=2时，y取得最小值-1，
∵当m≤x≤4时，总有-1≤y≤4m，
∴-14≤m≤2，
若0即有4m=42-4×4+3，
解得：m=34；
若-14≤m≤0，则当x=m时，y=4m，
即有4m=m2-4m+3
解得：m=4± 13，不合题意，
∴这种情况不存在，
综上所述，当m≤x≤4时，总有-1≤y≤4m，则m=34．
故选：D
11.【答案】0.90
【解析】仔细观察表格，发现大量重复试验发芽的频率逐渐稳定在0.90左右，从而得到结论．
【详解】解：∵观察表格，发现大量重复试验发芽的频率逐渐稳定在0.90左右，
∴该植物的种子发芽的概率为0.90，
故答案为：0.90．
12.【答案】33
【解析】本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．根据旋转的性质得到∠BOD=62∘，然后计算∠BOD-∠COD即可．
【详解】解：∵▵AOB绕点O逆时针旋转62∘得到△COD，
∴∠BOD=62∘，
∴∠BOC=∠BOD-∠COD=62∘-29∘=33∘．
故答案为：33．
13.【答案】4
【解析】设线段a，b的比例中项为c，根据比例中项的定义可知，c2=ab=2×8，求得c的值，注意两条线段的比例中项为正数．
【详解】解：设线段a，b的比例中项为c，
∵c是长度分别为2、8的两条线段的比例中项，
∴c2=ab=2×8，
即c2=16，
∴c=4(负数舍去)，
故答案为：4．
14.【答案】y=x+12-4
【解析】本题考查的是抛物线的平移．按照抛物线的平移规律：左加右减，上加下减，从而可得答案．
【详解】解：将抛物线y=(x-1)2-3先向左平移2个单位，再向下平移1个单位，得到的新抛物线的解析式是y=x-1+22-3-1即y=x+12-4．
故答案为：y=x+12-4．
15.【答案】6
【解析】解：如图，作OH⊥CD于H，连接AH，延长AH交BF于K，连接OC．
∵OH⊥CD，
∴CH=DH=4(cm)，∠CHO=90°，
∴OH= OC2-CH2= 52-42=3(cm)，
∵AE⊥CD，BF⊥CD，
∴AE//OH//BF，
∵OA=OB，
∴EH=FH，
∵∠AEH=∠KFH=90°，∠AHE=∠FHK，
∴△AEH≌△KFH(AAS)，
∴AH=HK，AE=FK，
∵AO=OB，
∴OH=12BK，
∴BK=6(cm)，
∴BF-AE=BF-FK=BK=6(cm)．
故答案为6．
如图，作OH⊥CD于H，连接AH，延长AH交BF于K，连接OC.证明AE=FK，利用勾股定理求出OH，再利用三角形的中位线定理求出BK即可解决问题．
本题考查垂径定理，勾股定理，平行线等分线段定理，三角形的中位线定理，全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考填空题中的压轴题．
16.【答案】5 2-5或5
【解析】解：∵△ABC中，∠A=90°，BC=5 2，∠B=45°
∴AB=AC=5，
由旋转性质可得：AB=DE=CD=5,BC=CE=5 2，
如图所示，
将三角板绕着点C顺时针旋转 45°后，DE/​/BC，
此时AE=CE-AC=5 2-5；
如图所示，
将三角板绕着点C顺时针旋转90°后，DE/​/AC，
∵DE/​/AC，DE=AC，
∴四边形ACDE是平行四边形，
∵∠CDE=90°，
∴四边形ACDE是矩形，
∴AE=CD=5，
故答案为：5 2-5或5．
据题意画出图形，分将三角板绕着点C顺时针旋转 45°及90°两种情况讨论，进行求解即可．
本题考查了旋转的性质，平行线的性质及矩形的判定与性质等，解题关键是能够根据题意画出图形，再利用相关性质解题．
17.【答案】解：(1)∵抛物线y=x2+bx+c经过点(-2,0)，(6,0)，
∴抛物线的对称轴为直线x=-2+62=2；
(2)∵抛物线的对称轴为直线x=2，a>0，开口向上，
则x≤2时，y随x的增大而减小．
【解析】(1)根据抛物线的对称性以及抛物线与坐标轴的交点，即可求解；
(2)根据抛物线开口向上，对称轴为直线x=2，可得x≤2时，y随x的增大而减小，即可求解．
本题考查了二次函数的性质，二次函数图象上点的坐标特征，熟练掌握二次函数的性质是解题的关键．
18.【答案】解：(1)列表如下：
所有等可能的情况数有12种，其中抽取的两张卡片数字和大于等于5的有8种，
则抽取的两张卡片数字和大于等于5的概率是812=23；
(2)列表如下：
所有等可能的情况数有12种，其中两张卡片上的数字都为奇数有2种，取出的两张卡片上的数字为一奇一偶有8种，
则甲胜的概率是212=16，乙胜的概率是812=23，
∵16≠23，
∴这个游戏不公平．
【解析】(1)根据题意列表得出所有等可能的情况数，找出符合条件的情况数，再根据概率公式即可得出答案；
(2)根据列表得出所有等可能的情况数，找出符合条件的情况数，根据概率公式求出甲和乙各获胜的概率，再进行比较，即可得出答案．
本题考查的是游戏公平性的判断．判断游戏公平性就要计算每个事件的概率，概率相等就公平，否则就不公平．用到的知识点为：概率=所求情况数与总情况数之比．
19.【答案】【小题1】
解：把A-6,1，B(2,1)代入y=12x2+mx+n，得，
12×-62-6m+n=112×22+2m+n=1
解得，m=2n=-5
∴抛物线的表达式为y=12x2+2x-5
【小题2】
解：y=12x2+2x-5=12x+22-7，
∴抛物线的对称轴为直线x=-2，
当x=-1时，y有最小值-132，
当x=2时，y的值为1，
∴当-1
【解析】1.
本题考查了待定系数法求二次函数的解析式，二次函数的性质，熟练掌握待定系数法是解题的关键．
利用待定系数法求二次函数的表达式；
2.
利用配方法得到y=12x+22-7，根据二次函数的性质得到抛物线的对称轴为直线x=-2，当x=-1时，y有最小值-132，当x=2时，y的值为1，从而可得结论．
20.【答案】【小题1】
证明：∵AB是⊙O的直径，
∴∠ACB=90∘，
∵OD//BC，
∴∠OFA=∠ACB=90∘，
∴OF⊥AC，
∴AD⌢=CD⌢，
∴点D为AC⌢的中点；
【小题2】
(解：∵OF⊥AC，AC=16，
∴AF=12AC=8，
在Rt▵AFO中，AO2=AF2+OF2，
∴OA2=64+OD-DF2，
∴OA2=64+OA-42，
∴OA=10，
∴⊙O的直径为20．

【解析】1.
根据圆周角定理、平行线的性质可得∠OFA=∠ACB=90∘，再根据垂径定理即可证明；
2.
根据垂径定理可得AF=12AC=8，再用勾股定理解Rt▵AFO即可．
21.【答案】【小题1】
解：设该函数的表达式为y=kx+b，根据题意，得：
30k+b=4032k+b=36,
解得
k=-2b=100,
∴y与x之间的关系式为y=-2x+100．
【小题2】
解：根据题意，得w=-2x+100x-20
=-2x2+140x-2000
=-2x-352+450，
∵a=-2<0，
∴当x=35时，w的值最大，
20<35<2×20，符合题意，
∴当销售单价为35元时，获得利润最大，最大利润是450元．

【解析】1.
本题考查了一次函数和二次函数的应用，解题的关键是找到题中的等量关系并列出函数解析式．
待定系数法求解一次函数解析式即可；
2.
根据题意得w=-2x+100x-20，计算求出满足要求的解即可．
22.【答案】【小题1】
解：①根据小球飞行的水平距离x(米)与小球飞行的高度y(米)的变化规律表可知，抛物线顶点坐标为4,8，
∴-b2a=4-b24a=8,
解得：a=-12b=4,
∴二次函数解析式为：y=-12x2+4x,
当y=152时，-12x2+4x=152,
解得：x=3或x=5(舍去)，
∴m=3,
当x=6时，n=y=-12×62+4×6=6,
故答案为：3，6；
②联立得：
y=-12x2+4xy=14x,
解得：x=0y=0或x=152y=158,
∴点A的坐标是152,158；
【小题2】
解：由题意可知小球飞行最大高度为8米，
∴y=-5t2+vt=-5t-v102+v220,
∴v220=8
解得：v1=4 10，v2=-4 10(负值舍去)，
∴v的值为4 10．

【解析】1.
本题主要考查二次函数的应用，待定系数法求二次函数的解析式等知识，从图象和表格中获取数据是解题的关键．
①由抛物线的顶点坐标为4,8可建立过于a，b的二元一次方程组，求出a，b的值即可；
②联立两函数解析式求解，可求出交点A的坐标；
2.
根据题意可知最大高度为8米，将小球飞行高度与飞行时间的函数关系式化简为顶点式即可求得v值．
23.【答案】【小题1】
连接OA，
由题意得：AD=12AB=30，OD=r-18
在Rt▵ADO中，由勾股定理得：r2=302+(r-18)2，
解得，r=34；
【小题2】
连接OA'，
∵OE=OP-PE=30，
∴在Rt▵A'EO中，由勾股定理得：A'E2=A'O2-OE2，
即：A'E2=342-302，
解得：A'E=16．
∴A'B'=32．
∵A'B'=32>30，
∴不需要采取紧急措施．

【解析】1.
连接OA，利用r表示出OD的长，在Rt▵AOD中根据勾股定理求出r的值即可；
2.
连接OA'，在Rt▵A'EO中，由勾股定理得出A'E的长，进而可得出A'B'的长，据此可得出结论．
24.【答案】【小题1】
∵点A(-5,0)在抛物线y=-x2-4x+c的图象上，
∴0=-52+4×5+c
∴c=5，
∴点C的坐标为(0,5)；
【小题2】
过P作PE⊥AC于点E，过点P作PF⊥x轴交AC于点H，如图：
∵A(-5,0)，C(0,5)
∴OA=OC，
∴▵AOC是等腰直角三角形，
∴∠CAO=45∘，
∵PF⊥x轴，
∴∠AHF=45∘=∠PHE，
∴▵PHE是等腰直角三角形，
∴PE=PH 2，
∴当PH最大时，PE最大，
设直线AC解析式为y=kx+5，
将A(-5,0)代入得0=5k+5，
∴k=1，
∴直线AC解析式为y=x+5，
设Pm,-m2-4m+5，(-5∴PH=-m2-4m+5-(m+5)=-m2-5m=-m+522+254，
∵a=-1<0，
∴当m=-52时，PH最大为254，
∴此时PE最大为25 28，即点P到直线AC的距离值最大；
【小题3】
存在．
∵y=-x2-4x+5=-(x+2)2+9
∴抛物线的对称轴为直线x=-2，
设点N的坐标为(-2,m)，点M的坐标为(x,-x2-4x+5)
分三种情况：①当AC为平行四边形ANMC的边时，如图，
∵A(-5,0)，C(0,5)，
∴xC-xA=xM-xN，即x-(-2)=0-(-5)
解得，x=3．
∴-x2-4x+5=-32-4×3+5=-16,
∴点M的坐标为(3,-16)
②当AC为平行四边形AMNC的边长时，如图，
方法同①可得，x=-7，
∴-x2-4x+5=-(-7)2-4×(-7)+5=-16,
∴点M的坐标为(-7,-16)；
③当AC为对角线时，如图，
∵A(-5,0)，C(0,5)，
∴线段AC的中点H的坐标为(-5+02,0+52)，即H(-52,52)
∴x+(-2)2=-52，解得，x=-3。
∴-x2-4x+5=-(-3)2-4×(-3)+5=8,
∴点M的坐标为(-3,8)
综上，点M的坐标为：(-3,8)或(3,-16)或(-7,-16)．

【解析】1.
把点A的坐标代入y=-x2-4x+c，求出c的值即可；
2.
过P作PE⊥AC于点E，过点P作PF⊥x轴交AC于点H，证明▵PHE是等腰直角三角形，得PE=PH 2，当PH最大时，PE最大，，运用待定系数法求直线AC解析式为y=x+5，设Pm,-m2-4m+5，(-53.
分①当AC为平行四边形ANMC的边，②当AC为平行四边形AMNC的边，③当AC为对角线三种情况讨论求解即可．
看书数量/(本)
2
3
4
5
6
人数/(人)
6
6
10
8
5
种子个数
100
400
900
1500
2500
4000
发芽种子个数
92
352
818
1336
2251
3601
发芽种子频率
0.92
0.88
0.91
0.89
0.90
0.90
x
30
32
34
36
y
40
36
32
28
x
0
1
2
m
4
5
6
7
y
0
3.5
6
7.5
8
7.5
n
3.5
1
2
3
4
1
---
3
4
5
2
3
---
5
6
3
4
5
---
7
4
5
6
7
---
1
2
3
4
1
---
(2,1)
(3,1)
(4,1)
2
(1,2)
---
(3,2)
(4,2)
3
(1,3)
(2,3)
---
(4,3)
4
(1,4)
(2,4)
(3,4)
---