专题37 空间点、直线、平面之间的位置关系-2025年高考数学一轮复习讲义（知识梳理+真题自测+考点突破+分层检测）（新高考专用）

这是一份专题37 空间点、直线、平面之间的位置关系-2025年高考数学一轮复习讲义（知识梳理+真题自测+考点突破+分层检测）（新高考专用），文件包含专题37空间点直线平面之间的位置关系-2025年高考数学一轮复习讲义知识梳理+真题自测+考点突破+分层检测新高考专用原卷版docx、专题37空间点直线平面之间的位置关系-2025年高考数学一轮复习讲义知识梳理+真题自测+考点突破+分层检测新高考专用解析版docx等2份试卷配套教学资源，其中试卷共72页， 欢迎下载使用。

【知识梳理】2
【真题自测】4
【考点突破】13
【考点1】基本事实的应用13
【考点2】空间位置关系的判断21
【考点3】异面直线所成的角28
【分层检测】35
【基础篇】35
【能力篇】47
【培优篇】52
考试要求：
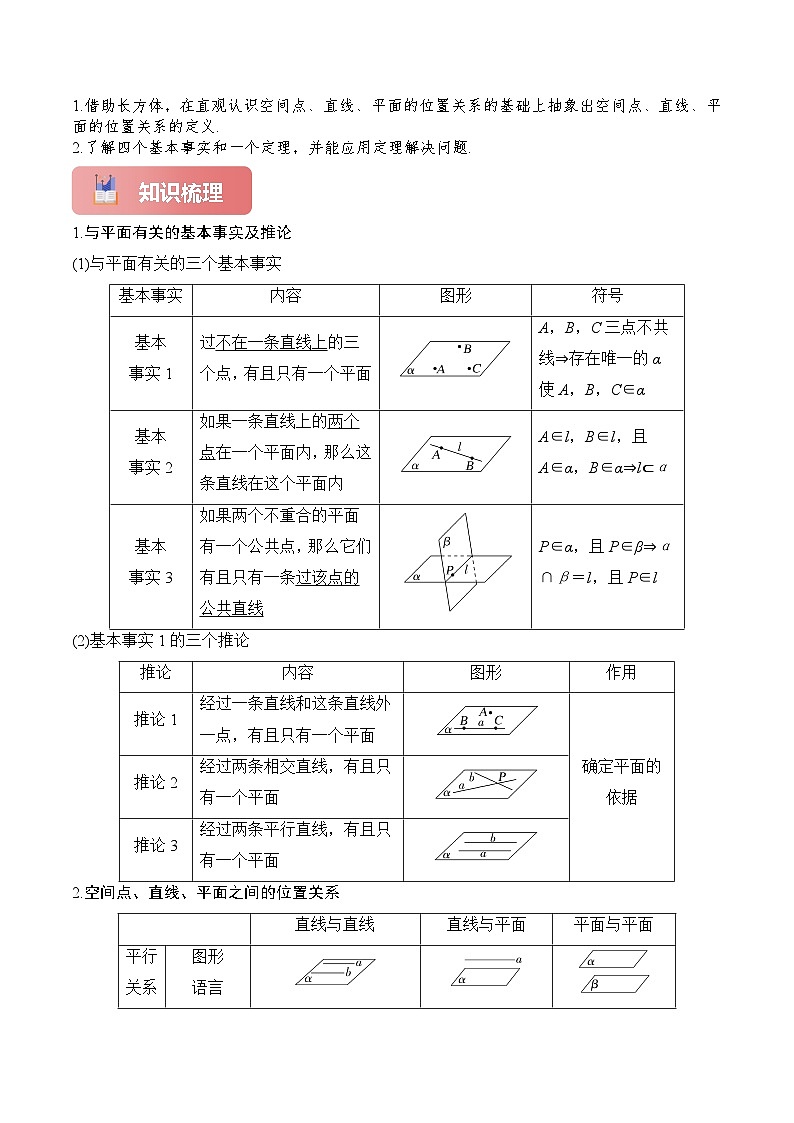
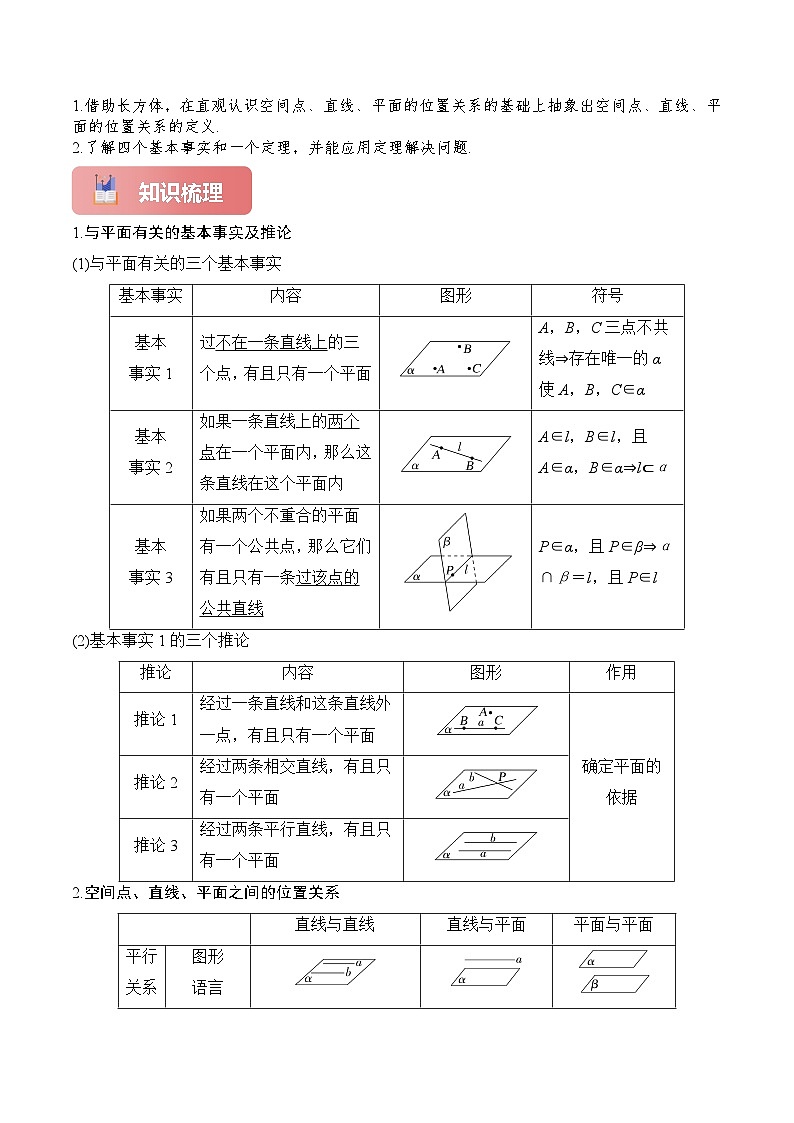
1.借助长方体，在直观认识空间点、直线、平面的位置关系的基础上抽象出空间点、直线、平面的位置关系的定义.
2.了解四个基本事实和一个定理，并能应用定理解决问题.
知识梳理
1.与平面有关的基本事实及推论
(1)与平面有关的三个基本事实
(2)基本事实1的三个推论
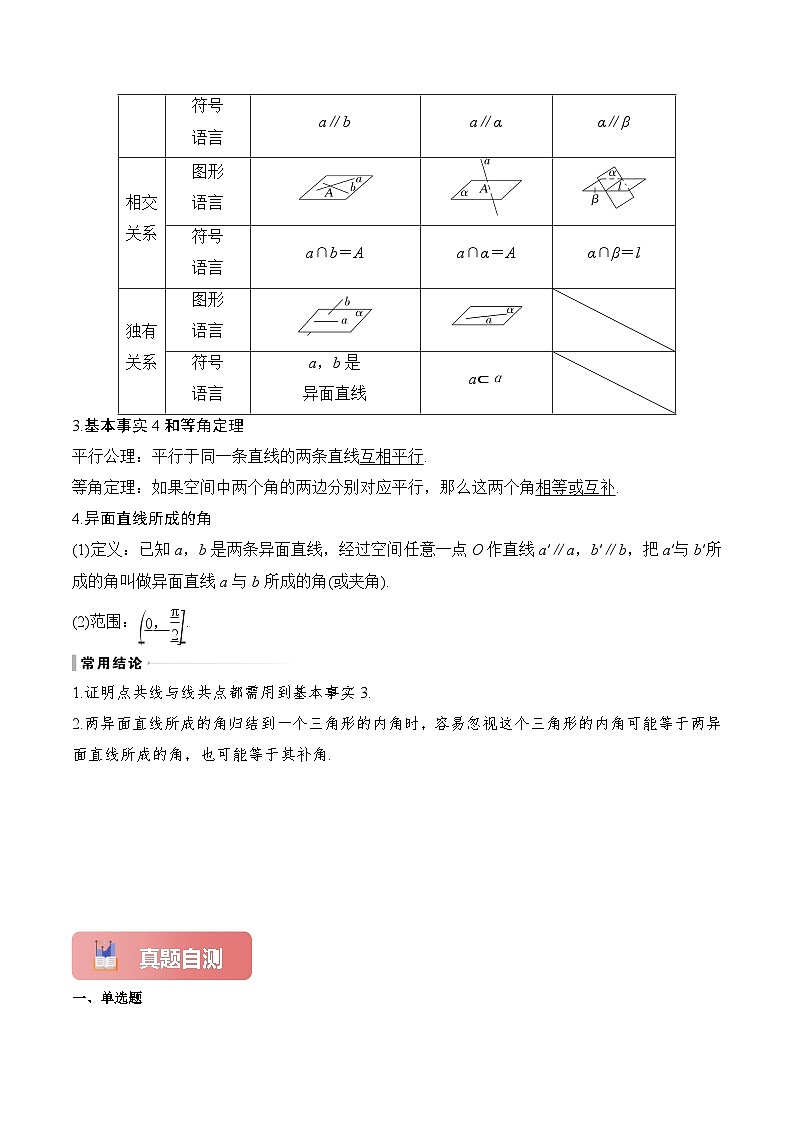
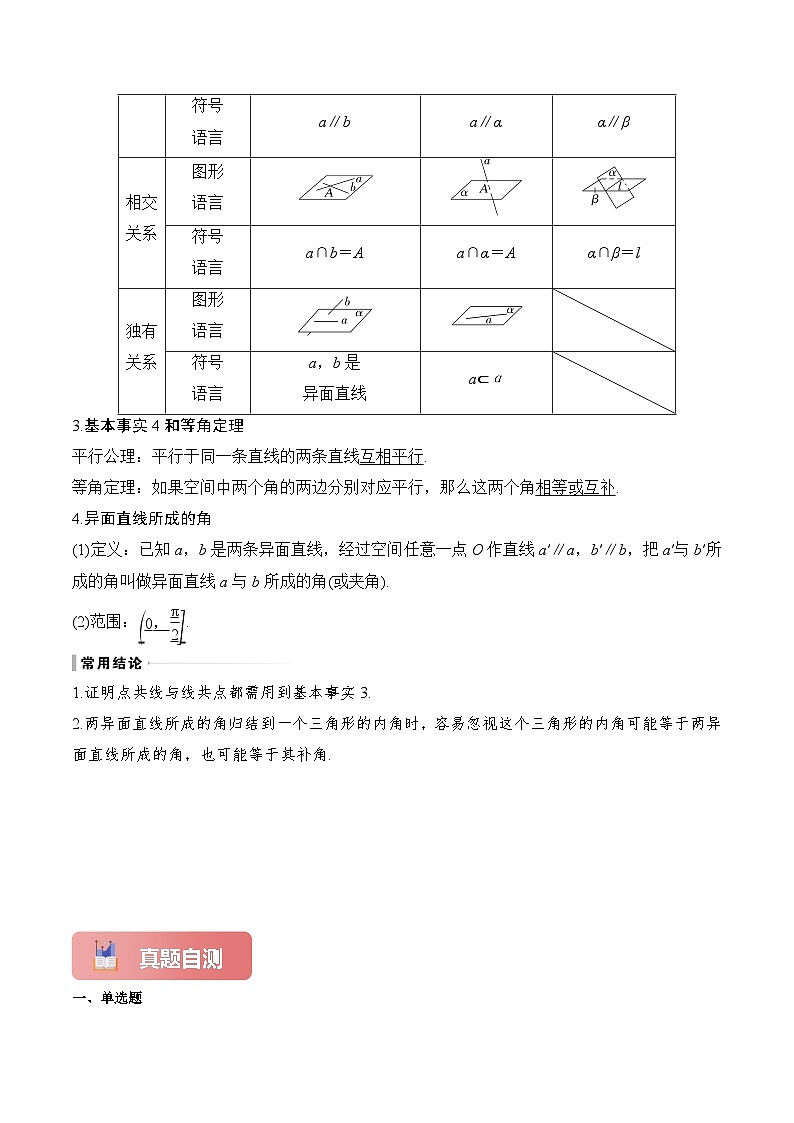
2.空间点、直线、平面之间的位置关系
3.基本事实4和等角定理
平行公理：平行于同一条直线的两条直线互相平行.
等角定理：如果空间中两个角的两边分别对应平行，那么这两个角相等或互补.
4.异面直线所成的角
(1)定义：已知a，b是两条异面直线，经过空间任意一点O作直线a′∥a，b′∥b，把a′与b′所成的角叫做异面直线a与b所成的角(或夹角).
(2)范围：eq \b\lc\(\rc\](\a\vs4\al\c1(0，\f(π,2))).
1.证明点共线与线共点都需用到基本事实3.
2.两异面直线所成的角归结到一个三角形的内角时，容易忽视这个三角形的内角可能等于两异面直线所成的角，也可能等于其补角.
真题自测
一、单选题
1．（2024·全国·高考真题）设为两个平面，为两条直线，且.下述四个命题：
①若，则或 ②若，则或
③若且，则 ④若与,所成的角相等，则
其中所有真命题的编号是（ ）
A．①③B．②④C．①②③D．①③④
2．（2024·天津·高考真题）若为两条不同的直线，为一个平面，则下列结论中正确的是（ ）
A．若，，则B．若，则
C．若，则D．若，则与相交
3．（2022·浙江·高考真题）如图，已知正三棱柱，E，F分别是棱上的点．记与所成的角为，与平面所成的角为，二面角的平面角为，则（ ）
A．B．C．D．
4．（2021·全国·高考真题）在正方体中，P为的中点，则直线与所成的角为（ ）
A．B．C．D．
二、多选题
5．（2022·全国·高考真题）已知正方体，则（ ）
A．直线与所成的角为B．直线与所成的角为
C．直线与平面所成的角为D．直线与平面ABCD所成的角为
6．（2021·全国·高考真题）如图，在正方体中，O为底面的中心，P为所在棱的中点，M，N为正方体的顶点．则满足的是（ ）
A．B．
C．D．
三、解答题
7．（2021·北京·高考真题）如图：在正方体中，为中点，与平面交于点．
（1）求证：为的中点；
（2）点是棱上一点，且二面角的余弦值为，求的值．
8．（2021·浙江·高考真题）如图，在四棱锥中，底面是平行四边形，，M，N分别为的中点，.
（1）证明：；
（2）求直线与平面所成角的正弦值.
参考答案：
1．A
【分析】根据线面平行的判定定理即可判断①；举反例即可判断②④；根据线面平行的性质即可判断③.
【详解】对①，当，因为，，则，
当，因为，，则，
当既不在也不在内，因为，，则且，故①正确；
对②，若，则与不一定垂直，故②错误；
对③，过直线分别作两平面与分别相交于直线和直线，
因为，过直线的平面与平面的交线为直线，则根据线面平行的性质定理知，
同理可得，则，因为平面，平面，则平面，
因为平面，，则，又因为，则，故③正确；
对④，若与和所成的角相等，如果，则，故④错误；
综上只有①③正确，
故选：A.
2．C
【分析】根据线面平行的性质可判断AB的正误，根据线面垂直的性质可判断CD的正误.
【详解】对于A，若，，则平行或异面或相交，故A错误.
对于B，若，则平行或异面或相交，故B错误.
对于C，，过作平面，使得，
因为，故，而，故，故，故C正确.
对于D，若，则与相交或异面，故D错误.
故选：C.
3．A
【分析】先用几何法表示出，再根据边长关系即可比较大小．
【详解】如图所示，过点作于，过作于，连接，
则，，，
，，，
所以，
故选：A．
4．D
【分析】平移直线至，将直线与所成的角转化为与所成的角，解三角形即可.
【详解】
如图，连接，因为∥，
所以或其补角为直线与所成的角，
因为平面，所以，又，，
所以平面，所以，
设正方体棱长为2，则，
，所以.
故选：D
5．ABD
【分析】数形结合，依次对所给选项进行判断即可.
【详解】如图，连接、，因为，所以直线与所成的角即为直线与所成的角，
因为四边形为正方形，则，故直线与所成的角为，A正确；
连接，因为平面，平面，则，
因为，，所以平面，
又平面，所以，故B正确；
连接，设，连接，
因为平面，平面，则，
因为，，所以平面，
所以为直线与平面所成的角，
设正方体棱长为，则，，，
所以，直线与平面所成的角为，故C错误；
因为平面，所以为直线与平面所成的角，易得，故D正确.
故选：ABD
6．BC
【分析】根据线面垂直的判定定理可得BC的正误，平移直线构造所考虑的线线角后可判断AD的正误.
【详解】设正方体的棱长为，
对于A，如图（1）所示，连接，则，
故（或其补角）为异面直线所成的角，
在直角三角形，，，故，
故不成立，故A错误.
对于B，如图（2）所示，取的中点为，连接，，则，，
由正方体可得平面，而平面，
故，而，故平面，
又平面，，而，
所以平面，而平面，故，故B正确.
对于C，如图（3），连接，则，由B的判断可得，
故，故C正确.
对于D，如图（4），取的中点，的中点，连接，
则，
因为，故，故，
所以或其补角为异面直线所成的角，
因为正方体的棱长为2，故，，
，，故不是直角，
故不垂直，故D错误.
故选：BC.
7．（1）证明见解析；（2）．
【分析】(1)首先将平面进行扩展，然后结合所得的平面与直线的交点即可证得题中的结论；
(2)建立空间直角坐标系，利用空间直角坐标系求得相应平面的法向量，然后解方程即可求得实数的值.
【详解】(1)如图所示，取的中点，连结，
由于为正方体，为中点，故，
从而四点共面，即平面CDE即平面，
据此可得：直线交平面于点，
当直线与平面相交时只有唯一的交点，故点与点重合，
即点为中点.
(2)以点为坐标原点，方向分别为轴，轴，轴正方向，建立空间直角坐标系，
不妨设正方体的棱长为2，设，
则：，
从而：，
设平面的法向量为：，则：
，
令可得：，
设平面的法向量为：，则：
，
令可得：，
从而：，
则：，
整理可得：，故（舍去）.
【点睛】本题考查了立体几何中的线面关系和二面角的求解问题，意在考查学生的空间想象能力和逻辑推理能力，对于立体几何中角的计算问题，往往可以利用空间向量法，通过求解平面的法向量，利用向量的夹角公式求解.
8．（1）证明见解析；（2）．
【分析】（1）要证，可证，由题意可得，，易证，从而平面，即有，从而得证；
（2）取中点，根据题意可知，两两垂直，所以以点为坐标原点，建立空间直角坐标系，再分别求出向量和平面的一个法向量，即可根据线面角的向量公式求出．
【详解】（1）在中，，，，由余弦定理可得，
所以，．由题意且，平面，而平面，所以，又，所以．
（2）由，，而与相交，所以平面，因为，所以，取中点，连接，则两两垂直，以点为坐标原点，如图所示，建立空间直角坐标系,
则,
又为中点，所以.
由（1）得平面，所以平面的一个法向量
从而直线与平面所成角的正弦值为．
【点睛】本题第一问主要考查线面垂直的相互转化，要证明，可以考虑，
题中与有垂直关系的直线较多，易证平面，从而使问题得以解决；第二问思路直接，由第一问的垂直关系可以建立空间直角坐标系，根据线面角的向量公式即可计算得出．
考点突破
【考点1】基本事实的应用
一、单选题
1．（2002·全国·高考真题）已知，为异面直线，平面，平面，，则（ ）
A．与，都相交B．与，中至少一条相交
C．与，都不相交D．至多与，中的一条相交
2．（2024·四川绵阳·模拟预测）如图所示，在正方体中，M是棱上一点，平面与棱交于点N.给出下面几个结论，其中所有正确的结论是（ ）
①四边形是平行四边形；②四边形可能是正方形；③存在平面与直线垂直；④任意平面都与平面垂直.

A．①②B．③④C．①④D．①②④
二、多选题
3．（2023·河北·模拟预测）如图，已知正方体的棱长为1，O为底面 ABCD的中心，交平面于点E，点 F为棱CD的中点，则（ ）
A．三点共线B．异面直线 BD与所成的角为
C．点到平面的距离为D．过点的平面截该正方体所得截面的面积为
4．（2022·全国·模拟预测）如图，在正方体中，，分别为，的中点，则（ ）
A．，，三条直线不可能交于一点，平面平面
B．，，三条直线一定交于一点，平面平面
C．直线与直线异面，平面平面
D．直线与直线相交，平面平面
三、填空题
5．（2024·山东济南·三模）在正四棱柱中，，，M，N分别是，的中点，则平面截该四棱柱所得截面的周长为 ．
6．（2021·全国·模拟预测）如图，在直三棱柱中，，D，E分别为，分如中点，则过点A，D，E的截面与三棱柱的侧面的交线的长为 ．
参考答案：
1．B
【分析】由题意画出满足条件的图象，结合图象得到正确选项.
【详解】若与都不相交，则，，则，这与是异面直线矛盾；
故C不正确；
如图，与中的一条相交，另一条不相交，

也可以与两条都相交，但不交于同一点，如图

综上：与中的至少一条相交.
故选：B
2．C
【分析】通过几何性质得出四边形的形状，由线线、线面垂直即可得出直线和平面与平面的关系.
【详解】对于①，因为平面与棱交于点，所以四点共面，
在正方体中，由平面平面，
又平面平面，平面平面，所以，
同理可得，故四边形一定是平行四边形，故①正确
对于②，在正方体中，面，
因为面，所以，
若是正方形， 有，，
若不重合，则与矛盾，
若重合，则不成立，故②错误；
对于③，因为平面，，
若直线与平面垂直，则直线，显然矛盾，
所以平面与直线不可能垂直，故③错误
对于④，因为平面，平面，所以，
又，平面，所以平面，
又平面，所以，
同理：，又平面，平面，，
所以平面，因为平面，所以平面平面，故④正确.
综上所述，正确的有①④.
故选：C.
3．ACD
【分析】由题意可证得三点都在平面与平面的交线上，可判断A；由题意可证得平面，从而，可判断B；由题意可证得平面，则的长度就是点到平面的距离，求解可判断C；取的中点，因为，所以等腰梯形就是过点的平面截该正方体所得截面，求出面积可判断D.
【详解】因为为底面ABCD的中心，所以为BD和AC的中点，则，
因为平面平面，所以平面平面，
所以点是平面与平面的公共点；
显然是平面与平面的公共点；
因为交平面于点平面，
所以也是平面与平面的公共点，
所以三点都在平面与平面的交线上，即三点共线，故A正确；
因为平面平面ABCD，所以，
又平面，
所以平面，又平面，
所以，即异面直线BD与所成的角为，故B不正确；
根据证明的方法，同理可得，
因为平面，
所以平面，则的长度就是点到平面的距离，
显然为正三角形的中心，因为正方体的棱长为1，
所以正三角形的边长为，所以，
又，所以,
即点到平面的距离为，故C正确；
取的中点，连，因为，
所以等腰梯形就是过点的平面截该正方体所得截面，如图：
因为，，
所以等腰梯形的高为，
所以等腰梯形的面积为，
即过点的平面截该正方体所得截面的面积为，故D正确．
故选：ACD．
4．BC
【分析】证明出面面，判断出多面体为三棱台，由棱台的结构特征得到，，三条直线一定交于一点.判断A，B；先证明出平面平面，由平面与平面不平行，得到平面与平面不垂直，判断C，D.
【详解】在正方体中，平面，
则.又，，所以平面，
又平面，所以平面平面.
因为，分别为，的中点，所以，
，，，
，，所以多面体为三棱台，
所以，，三条直线一定交于一点，故A错误，B正确；
由题意知与相交，所以与异面，
因为平面，平面，
所以平面平面，又平面与平面不平行，
所以平面与平面不垂直，故C正确，D错误.
故选：BC.
5．
【分析】作出辅助线，得到平面截该四棱柱所得截面为五边形，求出各边边长，相加得到答案.
【详解】延长相交于点，连接交于点，连接，
因为正四棱柱中，，，M，N分别是，的中点，
所以，，，
因为∽，，故，，
在上取点，连接，则，
同理可知，所以四边形为平行四边形，
故四点共面，
则平面截该四棱柱所得的截面为五边形，
，，
同理，
故截面周长为.

故答案为：
6．
【分析】首先根据平行线将平面进行扩展得到过点A，D，E的截面与三棱柱的侧面的交线为，确定点为线段的三等分点靠近的点，最后在直角三角形中求得线段的长度即可.
【详解】由题意将直三棱柱补成一个直四棱柱,
取中点，连接,显然，
取中点，连接，则，
所以A，D，F，E四点共平面，连接与的交点为，连接
所以过点A，D，F，E的截面与三棱柱的侧面的交线为，
因为，且,
所以点为线段的三等分点靠近的点，
因为，所以，
又D为中点，所以，
因为面,所以，
则.
故答案为：.
【点睛】本题主要考查截面问题，如需要将平面进行扩展，一般有两种方法，一是通过做平行线进行扩展，一种是找相交直线确定交线上的点进行扩展，在备考中注意多总结.
反思提升：
共面、共线、共点问题的证明
(1)证明共面的方法：先确定一个平面，然后再证其余的线(或点)在这个平面内.
(2)证明共线的方法：先由两点确定一条直线，再证其他各点都在这条直线上.
(3)证明线共点问题的常用方法是：先证其中两条直线交于一点，再证其他直线经过该点.
【考点2】空间位置关系的判断
一、单选题
1．（2023·浙江嘉兴·二模）已知正方体的棱长为为空间内一点且满足平面，过作与平行的平面，与交于点，则（ ）
A．1B．C．D．
2．（2021·全国·模拟预测）已知，，是三条不同的直线，，是两个不同的平面，则下列结论一定正确的是（ ）
A．若，，，，则
B．若，，则
C．若，，，则
D．若，，，则
二、多选题
3．（2024·浙江·三模）已知平面，，直线，若，，与所成的角为，则下列结论中正确的有（ ）
A．内垂直a的直线必垂直于
B．内的任意直线必垂直于内的无数条直线
C．b与所成的角为
D．b与内的任意一条直线所成的角大于等于
4．（23-24高二上·湖北恩施·期中）在棱长为2的正方体中，，分别为，的中点，则（ ）
A．异面直线与所成角的余弦值为
B．点为正方形内一点，当平面时，的最大值为
C．过点，，的平面截正方体所得的截面周长为
D．当三棱锥的所有顶点都在球的表面上时，球的表面积为
三、填空题
5．（2023·全国·模拟预测）已知是两个不同的平面，是平面外两条不同的直线，给出四个条件：①；②；③；④，以下四个推理与证明中，其中正确的是 .（填写正确推理与证明的序号）
（1）已知②③④，则①成立
（2）已知①③④，则②成立
（3）已知①②④，则③成立
（4）已知①②③，则④成立
6．（2022·北京平谷·模拟预测）设棱长为2的正方体，是中点，点、分别是棱、上的动点，给出以下四个结论：
①存在；
②存在平面；
③存在无数个等腰三角形；
④三棱锥的体积的取值范围是.
则所有结论正确的序号是 .
参考答案：
1．D
【分析】由题意知平面平面，可先令为中点，再证明当点为中点时，满足平面平面，即可轻易得出的值.
【详解】因为为空间内一点且满足平面，过作与平行的平面，与交于点，
所以∥平面,而平面，故平面平面.
在正方体中，如图所示，取中点为,中点为,连接，
假设为中点，则为等腰三角形，中点为,所以;
又因为,,所以，
中点为,中点为,所以,而,所以，，平面，
所以平面，平面,所以；
因为，，,平面，
所以平面，平面，所以平面平面，符合题意，
故为中点，.
故选：D.
2．D
【分析】根据空间中的线线，线面，面面关系一一分析即可.
【详解】对于A项，需要加上与相交才符合线面垂直的判定定理，故A错误；
对于B项，有可能，故B错误；
对于C项，与没有关系，斜交､垂直平行都有可能，故C错误；
对于D项，若，，则，而，故，故D正确.
故选：D.
3．ABD
【分析】由平面与平面垂直的性质定理可判断AB；线面位置关系可判断C；由最小角定理可判断D．
【详解】对于A选项，由平面与平面垂直的性质定理可知，内垂直a的直线必垂直于β，A正确；
对于B选项，在内作的垂线，则此垂线必垂直于，
自然也就垂直内的任意直线，这种垂线可以作无数条，所以B正确；
对于C选项，b与所成的角为，但b与的位置关系不确定，不能确定b与β所成的角，
特殊情况下可以是，所以C错误；
对于D选项，由最小角定理可知，线面角是线与面内的任意直线所成角中的最小的角，故D正确．
故选：ABD．
4．ACD
【分析】对于A：根据正方体的性质得出在中即为异面直线与所成的角，即可判定；对于B：取的中点的中点，连接，，，得到，，即可证明面面，则根据已知得出轨迹为线段，则过作，此时取得最小值，即可判定；对于C：过点的平面截正方体所得的截面图形为五边形，得出，，设，，以为原点，分别以方向为轴､轴､轴正方向建立空间直角坐标系，得出，，，的坐标，则可根据，列式得出，，即可得出，，在中得出，同理得出，在中得出，同理得出，在中得出，即可得出五边形的周长，即过点的平面截正方体所得的截面周长，即可判定；对于D：取的中点，则，过作，且使得，则为三棱锥的外接球的球心，则为外接球的半径，计算得出半径即可求出球的表面积，即可判定.
【详解】对于A选项，，
在中即为异面直线与所成的角，
，
异面直线与所成的角的余弦值为．故A正确；
对于B选项，取的中点的中点，取的中点，连接，，，

四边形为平行四边形，，，，
同理可得，
又面，面，面，面，
面，面，
又，面，
面面，
又面，面，
轨迹为线段，
在中，过作，此时取得最小值，
在中，，，，
在中，，，，
在中，，，，
如图，在中，，
即的最小值为，而的最大值为．故B错误；
对于C选项，过点的平面截正方体，
平面平面，则过点的平面必与与交于两点，
设过点的平面必与与分别交于、，
过点的平面与平面和平面分别交于与，，同理可得，
如图过点的平面截正方体所得的截面图形为五边形，
如图以为原点，分别以方向为轴､轴､轴正方向建立空间直角坐标系，
设，，
则，，，，，
，，，，
，，
，解得，
，，，，
在中，，，，同理：，
在中，，，，同理：
在中，，，
，
即过点的平面截正方体所得的截面周长为．故C正确；
对于D选项，如图所示，取的中点，则，过作，
且使得，则为三棱锥的外接球的球心，
所以为外接球的半径，
在中，，
，
．故D项正确，
故选：ACD．
【点睛】关键点睛：通过证明面面平行得到动点的轨迹，利用空间向量法确定点的位置是B、C的关键.
5．（1）（3）
【分析】由线面平行，垂直的判定定理和性质定理，以及面面平行的判定，性质定理判断即可，不正确的举出一个反例即可.
【详解】（1）若，，所以，因为，所以，（1）正确；
（2）若，，且是平面外的直线，则，又因为，所以与平行或相交，（2）错误；
（3）因为，，则，又因为，是平面外的直线，所以，（3）正确；
（4）若，，且是平面外的直线，则，又因为，则与平行或相交，（4）错误.
故答案为：（1）（3）
6．③④
【分析】结合正方体的性质，利用棱锥的体积公式以及空间向量的坐标运算逐一判断即可.
【详解】对于①：取中点P，当点N在上移动时，直线平面，同时当点M在直线AB上移动时平面，因为，故与不可能平行，①错误.
对于②：如图，以D为原点建立空间直角坐标系，所以，，,设，，
所以，，，
设平面的法向量为，
则即，令得，所以，
所以，故与平面不垂直，②错误.
对于③：令即，化简得，即，，，因为，所以该式在的范围中存在无数组解，故说明有无数组可使，故③正确.
对于④：根据等体积性质可知，所以该三棱锥高可以看作，所以体积的取值范围即底面积的取值范围，根据点M位置的变化可知，当点M在A点时最小，当点M在B点时最大，计算得，，所以，故④正确.
故答案为：③④
反思提升：
空间中两直线位置关系的判定，主要是异面，平行和垂直的判定.异面直线的判定可采用直接法或反证法；平行直线的判定可利用三角形(梯形)中位线的性质、基本事实4及线面平行与面面平行的性质定理；垂直关系的判定往往利用线面垂直或面面垂直的性质来解决.
【考点3】异面直线所成的角
一、单选题
1．（2024·江西南昌·二模）在三棱锥中，平面，，，，分别为，的中点，则下列结论正确的是（ ）
A．，是异面直线，B．，是相交直线，
C．，是异面直线，与不垂直D．，是相交直线，与不垂直
2．（2024·陕西西安·模拟预测）如图，这是一个正方体的平面展开图，在该正方体中，下列命题正确的是（ ）

A．B．C．D．
二、多选题
3．（2024·全国·模拟预测）如图，已知正三棱锥和正三棱锥的侧棱长均为．若将正三棱锥绕旋转，使得点分别旋转至点处，且四点共面，点分别位于两侧，则下列说法中正确的是（ ）

A．多面体存在外接球B．
C．平面D．点运动所形成的最短轨迹长大于
4．（2024·江西宜春·模拟预测）如图，在棱长为的正方体中，点在线段上运动，则（ ）
A．平面平面
B．三棱锥的体积为定值
C．异面直线与所成角的取值范围是
D．当为的中点时，三棱锥的外接球的表面积为
三、填空题
5．（2024·上海崇明·二模）已知底面半径为1的圆柱，是其上底面圆心，、是下底面圆周上两个不同的点，是母线．若直线与所成角的大小为，则 ．
6．（2022·重庆沙坪坝·模拟预测）如图，已知，是相互垂直的两条异面直线，直线与，均相互垂直，且，动点，分别位于直线，上，若直线与所成的角，三棱锥的体积的最大值为 .
参考答案：
1．A
【分析】先用定理判断，是异面直线，再证明与垂直，连接，即可得到平面，取的中点，连接，，从而得到、，即可证明平面，从而得解．
【详解】显然根据异面直线判定方法：经过平面外一点与平面内一点的直线与平面内不经过点的直线是异面直线．
下面证明与垂直：
证明：因为平面，平面，
所以，
因为，分别为的中点，连接，
所以，
因为，平面，
所以平面，
如图：取的中点，连接，，
因为平面，所以，
又因为，所以，
因为，
所以，
又因为为的中点，所以，
因为，平面，
所以平面，
又因为平面，所以．
故选：A．
2．A
【分析】将正方体的展开图重新组合成正方体，对选项逐个分析，判断易得只有A选项正确.
【详解】如图所示，将展开图重新组合成正方体. 显然. 因此A选项正确.

由图易得，显然与所成角非直角，因此异面直线与所成角也非直角，所以不成立. 因此B、C选项不正确.
由图易得，显然与相交，因此不成立. 因此D选项不正确.
故选：A
3．BCD
【分析】若多面体存在外接球，则球心必为的外心，由即可判断A；正三棱锥中侧棱互相垂直且相等，正三棱锥中侧棱互相垂直且相等，将正三棱锥放到正方体中，即可判断BCD．
【详解】若多面体存在外接球，则球心必为的外心，连接，，
则，平面，又平面，所以，
所以，
因为，所以多面体不存在外接球，故选项A错误；

因为正三棱锥和正三棱锥的侧棱长均为，
则正三棱锥中侧棱两两互相垂直且相等，正三棱锥中侧棱两两互相垂直且相等，
所以正三棱锥可以放到正方体中，当点分别旋转至点处，且四点共面，点分别位于两侧时，如图所示，
易知四边形为平行四边形，则，
又平面，且平面，所以平面，故C正确；
因为四边形为正方形，所以，所以，故B正确；

设交于点，则互相平分，，，
在中，，同理可得，
在中，，所以，
又因为点运动的最短轨迹是以的中点为圆心，半径为的圆弧，
所以点运动所形成的最短轨迹长大于．故选项D正确．
故选：BCD．
【点睛】关键点点睛：本题BC选项的关键是利用线面平行的判定得到平面，D选项的关键是得到点运动的最短轨迹是以的中点为圆心，半径为的圆弧.
4．ABD
【分析】直接利用正方体的性质，几何体的体积公式, 异面直线的夹角和外接球的表面积公式逐项判断即可.
【详解】对于，由正方体的性质，在、上的射影分别为、，
而，，则，，，
又平面ACD1
所以面，平面，所以平面平面，故正确；
对于，因为，平面，
所以点到平面的距离为定值，又的面积不变，
所以三棱锥的体积为定值，故正确；
对于，因为，
所以异面直线与所成的角就是直线与所成的角，
因为是等边三角形，
当与线段的两个端点重合时，直线与所成的角最小为，
当与线段的中点重合时，直线与所成的角最大为，
所以所求角的范围是，故错误；
对于，该正四面体的外接球即为正方体外接球，，
故所求球的表面积为，故正确.
故选：.
5．
【分析】因为，且，得到直线与所成角即为直线与所成角在直角中，即可求解.
【详解】如图所示，因为，且
则直线与所成角即为直线与所成角的大小为，可得,
在直角中，可得，即.
故答案为：.
6．/
【分析】根据直线三条直线两两垂直，将图形还原为长方体，再根据，可得即为直线与所成的角的平面角，由此可求得，从而可得，再根据棱锥的体积公式结合基本不等式即可得解.
【详解】因为直线三条直线两两垂直，
如图，将图形还原为长方体，
因为，所以即为直线与所成的角的平面角，
则，
因为平面，平面，所以，
在中，由，得，
所以，
，
当且仅当时，取等号，
所以三棱锥的体积的最大值为.
故答案为：.
【点睛】关键点点睛：根据直线三条直线两两垂直，将图形还原为长方体，从特殊几何体入手是解决本题的关键.
反思提升：
1.综合法求异面直线所成角的步骤：
(1)作：通过作平行线得到相交直线.
(2)证：证明所作角为异面直线所成的角(或其补角).
(3)求：解三角形，求出所作的角，如果求出的角是锐角或直角，则它就是要求的角；如果求出的角是钝角，则它的补角才是要求的角.
2.向量法：利用向量的数量积求所成角的余弦值.
分层检测
【基础篇】
一、单选题
1．（2024·安徽芜湖·三模）下列说法正确的是（ ）
A．正方体各面所在平面将空间分成27个部分
B．过平面外一点，有且仅有一条直线与这个平面平行
C．若空间中四条不同的直线满足，则
D．若为异面直线，平面平面，且与相交，若直线满足，则必平行于和的交线
2．（2024·上海·三模）如图，点N为正方形ABCD的中心，为正三角形，平面ECD⊥平面ABCD，M是线段EB的中点，则（ ）
A．DM≠EN，且直线DM、EN是异面直线
B．DM＝EN，且直线DM、EN是异面直线
C．DM≠EN，且直线DM、EN是相交直线
D．DM＝EN，且直线DM、EN是相交直线
3．（2020·四川眉山·二模）给出以下四个命题：
①依次首尾相接的四条线段必共面；
②过不在同一条直线上的三点，有且只有一个平面；
③空间中如果一个角的两边与另一个角的两边分别平行，那么这两个角必相等；
④垂直于同一直线的两条直线必平行.
其中正确命题的个数是（ ）
A．0B．1C．2D．3
4．（2024·山东日照·一模）已知l，m是两条不同的直线，为平面，，下列说法中正确的是（ ）
A．若l与不平行，则l与m一定是异面直线
B．若，则l与m可能垂直
C．若，且，则l与m可能平行
D．若，且l与不垂直，则l与m一定不垂直
二、多选题
5．（2024·云南昆明·模拟预测）如图是一个正方体的平面展开图，则在该正方体中（ ）
A．B．
C．与成60°角D．与是异面直线
6．（2024·山西运城·一模）设a、b是两条不同的直线，是两个不同的平面，则下列命题正确的有（ ）
A．若，则B．若，则
C．若，则D．若，则
7．（2024·广东深圳·二模）已知m，n是异面直线，，，那么（ ）
A．当，或时，
B．当，且时，
C．当时，，或
D．当，不平行时，m与不平行，且n与不平行
三、填空题
8．（20-21高二上·山西太原·阶段练习）下列命题中正确的命题为 .
①若在平面外，它的三条边所在的直线分别交于，则三点共线；
②若三条直线互相平行且分别交直线于三点，则这四条直线共面；
③若直线异面，异面，则异面；
④若，则.
9．（2024·江苏南通·二模）已知二面角为直二面角，，，，，则与，所成的角分别为，，与所成的角为 .
10．（2005·山东·高考真题）已知m、n是不同的直线，是不重合的平面，给出下列命题：
①若，则；
②若，则；
③若，则；
④m，n是两条异面直线，若，则．
上面的命题中，真命题的序号是 ．（写出所有真命题的序号）
四、解答题
11．（2022·陕西西安·模拟预测）如图，在正四面体A-BCD中，点E，F分别是AB，BC的中点，点G，H分别在CD，AD上，且，．
(1)求证：直线EH，FG必相交于一点，且这个交点在直线BD上；
(2)若，求点B到平面EFGH的距离．
12．（2023·广东汕头·二模）如图，正方体中，直线平面，，.
(1)设，，试在所给图中作出直线，使得，并说明理由；
(2)设点A与（1）中所作直线确定平面.
①求平面与平面ABCD的夹角的余弦值；
②请在备用图中作出平面截正方体所得的截面，并写出作法.
参考答案：
1．A
【分析】利用空间关系，可以判断AB，对于C可用正方体模型来举反例，对于D也是举反例.
【详解】对于A，利用四个侧面将空间分成九个部分，再由上下底面又将空间分成上中下三层，所以可以将空间分成27个部分，故A是正确的；
对于B，因为过平面外一点可以作一个平面与该平面平行，在这个平行平面内有无数条过该点的直线都与已知平面平行，故B是错误的；
对于C，
在正方体中，把看成，把看成，把看成，把看成，
它们满足，但不满足，故C是错误的；
对于D，由平面平面，且与相交于，则，
即满足条件，但此时与重合，它们不平行，故D是错误的；
故选：A.
2．D
【分析】连接，可得是的中点，可得与相交，进而可证，从而可得，从而可得.
【详解】连接，
因为点N为正方形ABCD的中心，所以是的中点，
所以平面，所以与相交，
因为四边形ABCD是正方形，所以，
又因为平面平面，平面平面，
所以平面，因为平面，所以，
又因为是等边三角形，所以，
所以，所以，又因为是的中点，
所以.
故选：D.
3．B
【解析】用空间四边形对①进行判断；根据公理2对②进行判断；根据空间角的定义对③进行判断；根据空间直线位置关系对④进行判断.
【详解】①中，空间四边形的四条线段不共面，故①错误.
②中，由公理2知道，过不在同一条直线上的三点，有且只有一个平面，故②正确.
③中，由空间角的定义知道，空间中如果一个角的两边与另一个角的两边分别平行，那么
这两个角相等或互补，故③错误.
④中，空间中，垂直于同一直线的两条直线可相交，可平行，可异面，故④错误.
故选：B
【点睛】本小题考查空间点，线，面的位置关系及其相关公理，定理及其推论的理解和认识；考查空间想象能力，推理论证能力，考查数形结合思想，化归与转化思想.
4．B
【分析】根据空间中线、面位置关系分析逐项分析判断.
【详解】对于选项A：若l与不平行，则l与的位置关系有：相交或直线在平面内，
且，则l与m的位置关系有：平行、相交或异面，故A错误；
对于选项B：若，则l与m可能垂直，
如图所示：，可知：，故B正确；

对于选项C：若，且，，则l与m异面，故C错误；
对于选项D：若，且l与不垂直，则l与m可能垂直，
如图，取为平面，，

符合题意，但，故D错误；
故选：B.
5．BCD
【分析】由展开图翻折成正方体，根据正方体的性质判断直线间的位置关系．
【详解】展开图翻折成的正方体如图所示，因为，，因此，所以A错误；同理，，所以，B正确；
或其补角是与所成的角，又△是等边三角形，所以，所以与所成的角是，C正确.
又平面，且与不平行，故与是异面直线，D正确.
故选：BCD.
6．BCD
【分析】利用空间中线线关系，线面关系，面面关系，分别判断即可.
【详解】对于选项A，因为，所以或与相交或与异面，故选项A错误；
对于选项B，因为，根据垂直于同一平面的两直线平行，所以，故选项B正确；
对于选项C，因为，所以与内的某条直线平行，又，所以，
又，，所以，故选项C正确；
对于选项D，因为，所以与内的某条直线平行，
因为，所以直线与内的某条直线平行，所以，
因为，，所以，故选项D正确.
故选：BCD.
7．AB
【分析】根据线线、线面和面面之间的基本关系，结合选项依次判断即可.
【详解】A：当，时，；
当，时，，故A正确；
B：当，时，又为异面直线，所以，故B正确；
C：当时，由，得或与相交；
当时，由，得或与相交，故C错误；
D：当不平行时，可能或与相交，或与相交，故D错误.
故选：AB
8．①②
【分析】根据三点共线和共面的性质、异面直线的性质、垂直的性质逐一判断即可.
【详解】对于①，设平面平面，因为，所以平面，
所以，同理，，故三点共线，①正确；
对于②，因为，所以可以确定一个平面，
因为所以，所以，又，
所以，因为，所以或，又，
所以不成立，所以，即这四条直线共面，所以②正确；
对于③，直线异面，异面，但是平行，所以③错误，如下右图；
对于④，，但，所以④错误，如下左图.
故正确的命题为①②.
故答案为：①②
9．/
【分析】如图，设，根据勾股定理求得，，建立如图空间直角坐标系，利用空间向量法求解线线角即可.
【详解】如图，
，则两两垂直.
作，垂足分别为，连接，
则，
所以为与的所成角，为与的所成角，
即，，
建立如图空间直角坐标系，设，
则，得，
，所以，取，
则，又，
所以，即与所成的角为.
故答案为：
10．③④
【分析】利用平面与平面平行的判定和性质可判断各命题的真假．
【详解】若，则m与n平行或异面，故①错误；
，但m与n不一定相交，不一定成立，故②错误；
若，则，又由，则，故③正确；
m，n是两条异面直线，若，则过m的平面与平面相交于直线，有，过n的平面与平面相交于直线，有，m，n异面，一定相交，，如图所示，
由面面平行的判定可知，故④正确；
故答案为：③④
11．(1)证明见解析；
(2)．
【分析】（1）根据公理2的推论可知，E，F，G，H四点共面，再根据公理3即可证出；
（2）根据等积法即可求出．
【详解】（1）因为，，所以，又，所以，故E，F，G，H四点共面，且直线EH，FG必相交于一点，设，因为，平面ABD，所以M∈平面ABD，同理：平面BCD，而平面平面，故平面BCD，即直线EH，FG必相交于一点，且这个交点在直线BD上．
（2）连结EG，BG，点B到平面EFGH的距离为d，正四面体的棱长为2易知该正四面体的高为，所以E到平面BFG的距离为，在△CFG中，由余弦定理可得：，在等腰梯形EFGH中可得：G到EF的距离为，而G到BF的距离也为，则．
由可得：，故点B到平面EFGH的距离为．
12．(1)答案见解析；
(2)①；②答案见解析.
【分析】（1）取和中点分别为P、Q，利用正方体的性质结合线面垂直的判定定理可得平面，进而即得；
（2）利用坐标法，根据面面角的向量求法即得；设直线交于，连接分别交于，进而可得截面.
【详解】（1）由题意，P、Q分别为和的中点时，有，
证明过程如下：连接，取和中点分别为P、Q，连接，
∵，∴一定过经过点E,∴PQ即为所求作的l.
∵P、Q分别为和的中点，∴P、Q为的中位线，
∴，且PQ过经过点E，
∵正方体的的上底面为正方形.
∴，∵，∴，
又∵正方体的侧棱垂直底面，，
∴，又∵，平面，.
∴平面，∵平面，
∴，即；
（2）①连接AP，AQ，∵正方体中，有AD，DC，DD两两垂直，以D点为坐标原点，建立空间直角坐标系，如图所示，
设正方体边长为2，则有，，，，，
所以，，
∵正方体的侧棱垂直底面ABCD，∴为平面ABCD的法向量.
设平面，即平面APQ的法向量，则，.
∴，，即
令，则，.
∴平面APQ的一个法向量.
，，，
设平面与平面ABCD的夹角的平面角为，
则；
②设直线交于，连接分别交于，连接，则平面即为平面截正方体所得的截面，如图所示.
【能力篇】
一、单选题
1．（2023·天津和平·三模）已知正方体的棱长为6，点，分别在棱，上，且满足，点为底面的中心，过点，，作平面，则平面截正方体所得的截面面积为（ ）
A．B．C．D．
二、多选题
2．（2024·全国·模拟预测）已知是两条不同的直线，是两个不同的平面，则（ ）
A．若，则B．若，则与为异面直线
C．若，则D．若，则
三、填空题
3．（2006·四川·高考真题），是空间两条不同的直线，，是空间两个不同平面，下面有四个命题：
①，，；
②，，
③，，；
④，，．
其中真命题的编号是 ．
四、解答题
4．（2024·浙江·三模）在四棱锥中，，，，，、分别为直线，上的动点.
(1)若异面直线与所成的角为，判断与是否具有垂直关系并说明理由；
(2)若，，求直线与平面所成角的最大值.
参考答案：
1．A
【分析】由于上下底平行，则可得平面与上下底面的交线平行，则可得为平面与上底面的交线，为平面与下底面的交线，则梯形为平面截正方体的截面，可证得梯形为等腰梯形，根据已知的数量关系求解即可.
【详解】连接，，与交点即为，
因为，所以‖，
因为‖，所以‖，
所以共面，
所以平面截正方体所得的截面为梯形，
因为正方体的棱长为6，且，
所以，
在中，，则，
在中，，则
，
在，，则
，
过作于，则，
所以,
所以等腰梯形的面积为
,
故选：A

2．AD
【分析】运用线面平行的性质定理和面面平行的判定定理可推理A项正确，利用线面平行的性质定理和线面垂直的性质定理可推理D项正确，B , C两项可以通过举反例说明其错误.
【详解】对于A项，因，经过直线可作平面，使，则，因，则，又，故得，即A项正确；
对于B项，若，则与可能相交、平行或异面，故B项错误；
对于C项，若，则或，故C项错误；
对于D项，因，经过直线可作平面，使，则，又，，则，故得，即D项正确．
故选：AD．
3．①④
【解析】利用在内有与平行的直线，判断①正确；因为，，根据可能，判断②错误；由可能且，判断③错误；由，，，可得，判断④正确.
【详解】①因为，；所以在内有与平行的直线，又，则，故①正确；
②因为，，所以，又因为，则可能，故②错误；
③因为，，，所以可能且，故③错误；
④因为，，，所以，故④正确.
故答案为：①④
【点睛】本题考查空间内的直线与平面的平行关系和垂直关系，是基础题.
4．(1)答案见解析，理由见解析
(2)
【分析】（1）取的中点，连接，，即可说明，则（或其补角）为异面直线与所成的角，分和两种情况讨论，利用线面垂直的判定定理证明即可；
（2）以为坐标原点建立空间直角坐标系，设，求出平面的法向量，利用空间向量法求出线面角的正弦值，即可求出线面角的最大值.
【详解】（1）取的中点，连接，，
因为，，所以且，
所以四边形为平行四边形，
所以，所以（或其补角）为异面直线与所成的角，
①当时，在中，，，
由余弦定理可知，
所以，所以，所以，
又，，，平面，
所以平面，又平面，所以.
②当，假设，则由①有平面，
因为平面，所以，，
这与相矛盾，故此时与不垂直.
综上所述，当时，；当时，与不垂直.
（2）由，点是中点，可得，
从而由可得，
又，
所以，即，
因为，由（1）有，
所以，
所以两两互相垂直，
故可以为坐标原点，，，分别为轴，轴，轴建立空间直角坐标系.
故，，，，.
因为，设平面的法向量为，则有
设，则，又，所以有
令，则，故平面的一个法向量为，
设直线与平面所成的角为，则
，
令，则
当时，；
当时，.
（当且仅当，时取“＝”）.又，所以.
综上所述，直线与平面所成角的最大值为.
【培优篇】
一、单选题
1．（2024·四川成都·三模）六氟化硫，化学式为，在常压下是一种无色、无臭、无毒、不燃的稳定气体，有良好的绝缘性，在电器工业方面具有广泛用途.六氟化硫分子结构为正八面体结构（正八面体每个面都是正三角形，可以看作是将两个棱长均相等的正四棱锥将底面粘接在一起的几何体）.如图所示，正八面体的棱长为，下列说法中正确的个数有（ ）
①异面直线与所成的角为45°；
②此八面体的外接球与内切球的体积之比为；
③若点为棱上的动点，则的最小值为；
④若点为四边形的中心，点为此八面体表面上动点，且，则动点的轨迹长度为.
A．1个B．2个C．3个D．4个
二、多选题
2．（2024·全国·模拟预测）已知平行六面体的所有棱长都相等，，，，，且点E，F满足，，平面α过点A，E，F，则（ ）
A．
B．的面积是
C．平面α与平面的交线长为
D．点C到平面α的距离是点到平面α的距离的5倍
三、填空题
3．（2024·广东汕头·一模）如图，在正方体中，是棱的中点，记平面与平面的交线为，平面与平面的交线为，若直线分别与所成的角为，则 ， .
参考答案：
1．B
【分析】对①：借助等角定理，找到与平行，与相交的线段，计算即可得；对②：借助外接球与内切球的性质计算即可得；对③：空间中的距离和的最值问题可将其转化到同意平面中进行计算.对④，计算的值，并比较它们的大小，即可得出当点在平面内时，点在三角形的内切圆上运动，结合对称性即可验算.
【详解】对①：连接，取中点，连接、，
由题意可得、为同一直线，、、、四点共面，
又，故四边形为菱形，
故，故异面直线与所成的角等于直线与所成的角，
即异面直线与所成的角等于，故①错误；
对②：由四边形为正方形，有，
故四边形亦为正方形，即点到各顶点距离相等，
即此八面体的外接球球心为，半径为，
设此八面体的内切球半径为，
则有，化简得，
则此八面体的外接球与内切球的体积之比为，故②正确；
对③：将延折叠至平面中，如图所示：
则在新的平面中，、、三点共线时，有最小值，
则，故③错误.
对于④，设三角形的内切圆半径为，则由等面积法，有，
解得，
由②可知，点到平面的距离为，
所以，
这表明当点在平面内时，点在三角形的内切圆上运动，
它的周长是，
根据对称性可知动点的轨迹长度为，故④正确.
正确的编号有②④.
故选：B.
【点睛】关键点点睛：本题④中，关键点在于得出当点在平面内时，点在三角形的内切圆上运动，根据对称性即可顺利得解.
2．ACD
【分析】根据空间向量的模长关系的运算，即可得六面体的棱长，从而确定的面积，即可判断B；连接AC，交BD于点O，连接，根据线面关系可得平面，再由即可得，即可判断A；根据空间中直线与平面的关系，确定平面α与平面的交线，即可求长度，从而判断C；根据线段长度关系，可得点C到平面α的距离是点到平面α的距离的倍数关系，即可判断D.
【详解】由题意知．将的两边平方，得，
所以，即平行六面体的棱长为2，所以是边长为2的正三角形，
其面积为，B错误．
如图，连接AC，交BD于点O，连接，
则，．又，AC，平面，所以平面．
又平面，所以．因为，所以，A正确．
连接AE，EF，延长EF与的延长线交于点G，则，所以．
过点G作AE的平行线，与交于点H，与交于点M，连接AM，则平面α与平面的交线即为MH．
易知，，．
在中，由余弦定理，得
，C正确．
由可得点C到平面α的距离是点到平面α的距离的5倍，D正确．
故选：ACD．
【点睛】关键点点睛：本题考查平行六面体与空间向量、空间中的直线与平面的关系问题.解决本题的关键是利用空间向量的运算确定平行六面体的棱长、角度关系，从而可结合平行六面体的线面关系得线线垂直、得面面交线、得点到平面的距离关系.
3． /0.5 /
【分析】利用平面基本事实作出直线，进而求出；利用面面平行的性质结合等角定理，再利用和角的正切计算即得.
【详解】在正方体中，是棱的中点，
延长与延长线交于点，连接，则直线即为直线，，
由，得，又，于是，
由平面平面，平面平面，平面平面，
则，又，因此，，
所以.
故答案为：；
【点睛】关键点睛：利用平面的基本事实作出直线是求出角的关键.
基本事实
内容
图形
符号
基本
事实1
过不在一条直线上的三个点，有且只有一个平面
A，B，C三点不共线⇒存在唯一的α使A，B，C∈α
基本
事实2
如果一条直线上的两个点在一个平面内，那么这条直线在这个平面内
A∈l，B∈l，且A∈α，B∈α⇒l⊂α
基本
事实3
如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线
P∈α，且P∈β⇒α∩β＝l，且P∈l
推论
内容
图形
作用
推论1
经过一条直线和这条直线外一点，有且只有一个平面
确定平面的依据
推论2
经过两条相交直线，有且只有一个平面
推论3
经过两条平行直线，有且只有一个平面
直线与直线
直线与平面
平面与平面
平行关系
图形
语言
符号
语言
a∥b
a∥α
α∥β
相交关系
图形
语言
符号
语言
a∩b＝A
a∩α＝A
α∩β＝l
独有关系
图形
语言
符号
语言
a，b是
异面直线
a⊂α