2022-2023学年广东省深圳市罗湖区六年级下册期中数学试卷及答案

这是一份2022-2023学年广东省深圳市罗湖区六年级下册期中数学试卷及答案，共14页。试卷主要包含了一种药水按药和水1，在比例尺是1等内容，欢迎下载使用。
1．950dm2＝ m2 780cm3＝ L 5.6m3＝ cm3
2．如图是一个直角三角形，以6 cm的直角边所在直线为轴旋转一周，所得到的图形是 ，它的体积是 cm3。
3．把一个圆柱形纸盒的侧面沿高剪开，得到下面的图形，这个圆柱形纸盒的底面半径是 cm，它的侧面积是 cm2。
4．把一个棱长6分米的正方体钢锭熔铸成一个底面积是54平方分米的圆锥，圆锥的高是 分米。
5．
（1）如果5A＝6B（A、B均不为0），那么B：A＝ ： 。
（2）36的因数有 ，从中选4个不同的数组成比例是 （写出一个即可）。
6．选填“成正”、“成反”或“不成”。
圆的周长和圆的半径 比例；
利率一定，存款的本金和利息 比例；
修一条路，平均每天修的米数和所需天数 比例。
7．一种药水按药和水1：100配制，现配制这种药水5050g，需加入药 g。
8．将底面周长为62.8cm，高为20cm的圆柱沿直径切开，表面积增加 。
9．在比例尺是1：4000000的中国地图上，量得两地的距离是30厘米，这两地的实际距离是 千米。
10．一个长方形长10cm、宽6cm，按1：2缩小后的长方形的面积是 cm2。
11．甲数的25%等于乙数的，甲数和乙数的比是（ ）
A．25%：B．8：5C．5：8
12．下列各数量关系中，成正比例关系的是（ ）
A．买足球的个数和钱数
B．运送一批货物，运走的吨数和剩下的吨数
C．分子一定，分母和分数值
D．圆柱的侧面积一定，底面半径和圆柱的高
13．有一个圆柱体，底面半径是5cm，若高增加2cm，则圆柱的侧面积增加（ ）
A．15cm2B．31.4cm2C．62.8cm2D．78.5cm2
14．如果正方体、圆柱、圆锥的底面积相等，高也相等。下面说法正确的是（ ）。
A．圆柱的体积比正方体的体积小B．圆柱和正方体的表面积相同
C．圆柱的体积是圆锥的 D．圆锥的体积是正方体的
15．根据ab＝cd，下面不能组成比例的是（ ）
A．a：c＝d：bB．d：a＝b：cC．b：d＝a：cD．a：d＝c：b
16．将图形 绕点O逆时针旋转90°得到的图形是（ ）。
A．B．C．D．
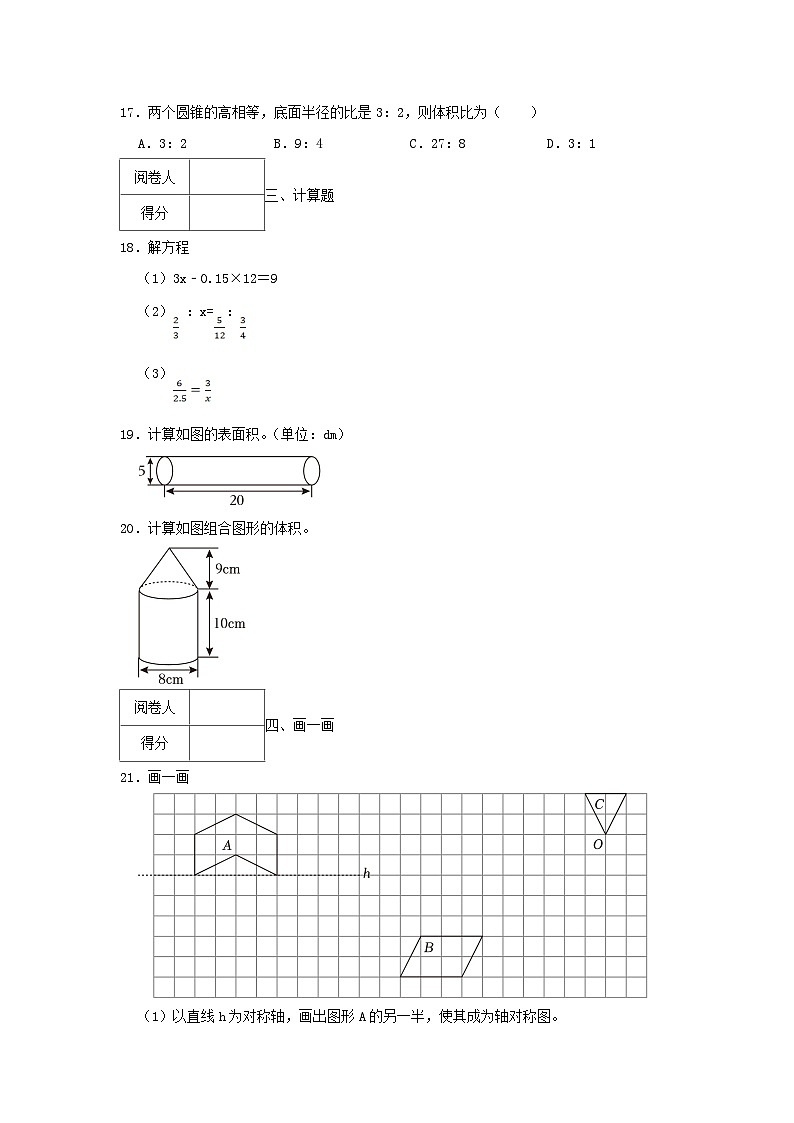
17．两个圆锥的高相等，底面半径的比是3：2，则体积比为（ ）
A．3：2B．9：4C．27：8D．3：1
18．解方程
（1）3x﹣0.15×12＝9
（2） ：x=：
（3）
19．计算如图的表面积。（单位：dm）
20．计算如图组合图形的体积。
21．画一画
（1）以直线h为对称轴，画出图形A的另一半，使其成为轴对称图。
（2）画出图形B按2：1的比放大后的图形。
（3）画出将图形C绕O点顺时针旋转90°，再向左平移4格后的图形。
22．爸爸打算给笑笑的小书房铺上方砖，用边长2分米的方砖需要90块，如果改用边长3分米的方砖，需要方砖多少块？（用比例解）
23．有一个周长80米的长方形花坛，长与宽的比是3：2。用1：1000的比例尺画在图纸上，长和宽各应画多少厘米？
24．一个盛水的圆柱形容器，底面直径是10cm，此时水深20cm。将一块石头完全浸没在水中，水面升高到24cm（水没有溢出），这块石头的体积是多少立方厘米？
25．一个圆锥形沙堆，它的底面半径是2米，高与底面半径的比是3：1，用这堆沙子在8m宽的公路上铺4cm厚的路面，能铺多少米？
26．磁悬浮列车匀速行驶，时间和路程的关系如下表。
（1）补充表格，然后在如图中描点，再顺次连接。
（2）时间和路程成什么比例？为什么？
（3）列车行驶4分半时，所行路程是多少千米？
答案解析部分
1．【答案】9.5；0.78；5600000
【知识点】含小数的单位换算；体积单位间的进率及换算；容积单位间的进率及换算
【解析】【解答】解：950dm2＝9.5m2；780cm3＝0.78L；5.6m3＝5600000cm3。
故答案为：9.5；0.78；5600000。
【分析】1平方米=100平方分米，1升=1000立方厘米，1立方米=1000000立方厘米，根据这些单位之间的进率换算单位即可。
2．【答案】圆锥；25.12
【知识点】圆锥的体积（容积）
【解析】【解答】解：如图，以6cm的直角边所在直线为轴旋转一周，会得到一个高是6cm、底面半径是2cm的圆锥，它的体积是：（cm3）。
故答案为：圆锥；25.12.
【分析】把一个直角三角形以某一直角边所在直线为轴旋转一周，会得到一个以这条直角边为高、另一条直角边为底面半径的圆锥。圆锥的体积=×底面积×高。π在计算时一般取3.14。
3．【答案】2；100.48
【知识点】圆柱的侧面积、表面积
【解析】【解答】解：底面半径：12.56÷3.14÷2=2（cm），侧面积：12.56×8=100.48（cm2）。
故答案为：2；100.48。
【分析】底面周长是12.56cm，高是8cm，用底面周长除以3.14再除以2即可求出底面半径；用底面周长乘高即可求出侧面积。
4．【答案】12
【知识点】正方体的体积；圆锥的体积（容积）
【解析】【解答】解：圆锥的高是6×6×6×3÷54=12分米。
故答案为：12。
【分析】因为是用正方体熔铸成的圆锥，所以它们的体积相等，正方体的体积=棱长×棱长×棱长，圆锥的体积=×底面积×高，据此作答即可。
5．【答案】（1）5；6
（2）1，2，3，4，6，9，12，36；2：3＝6：9
【知识点】因数的特点及求法；比例的认识及组成比例的判断；比例的基本性质
【解析】【解答】解：（1）如果5A＝6B（A、B均不为0），那么B：A＝5：6；
（2）36的因数有1，2，3，4，6，9，12，36，从中选4个不同的数组成比例是2：3=6：9。
故答案为：（1）5；6；（2）1，2，3，4，6，9，12，36；2：3=6：9（答案不唯一）。
【分析】（1）把5和A看作内项，则6和B就是两个外项，根据比例的基本性质写出比例即可；
（2）先找出36的所有因数，然后写出两个比值相等的比并组成比例即可。
6．【答案】成正；成正；成反
【知识点】成正比例的量及其意义；成反比例的量及其意义
【解析】【解答】解：圆周长÷半径=2π（一定），所以圆的周长和圆的半径成正比例；
利息÷本金=利率（一定），存款的本金和利息成正比例；
平均每条修的米数×所需天数=这条路的总长度，修一条路，平均每天修的米数和所需天数成反比例。
故答案为：成正；成正；成反。
【分析】根据数量关系判断相关联的两个量的商一定还是乘积一定，如果商一定就成正比例，如果乘积一定就成反比例，否则不成比例。
7．【答案】50
【知识点】比的应用
【解析】【解答】解：5050÷（1+100）
=5050÷101
=50（g）
故答案为：50。
【分析】药是1份，水是100份，用这种药水的总重量除以药和水的总份数即可求出1份是多少，也就是药的重量。
8．【答案】800平方厘米
【知识点】圆柱的侧面积、表面积
【解析】【解答】解：62.8÷3.14×20×2
=20×20×2
=800（平方厘米）
故答案为：800平方厘米。
【分析】沿着直径切开，表面积会增加两个相同的长方形的面。每个面的长是底面直径，宽就是圆柱的高。由此用底面周长除以3.14求出底面直径，用底面直径乘高求出一个面的面积，再乘2即可求出表面积增加的2个面的面积。
9．【答案】1200
【知识点】应用比例尺求图上距离或实际距离
【解析】【解答】解：30÷=120000000（厘米）=1200（千米）
故答案为：1200。
【分析】用图上距离除以比例尺即可求出实际距离，注意换算单位，1千米=100000厘米。
10．【答案】15
【知识点】图形的缩放；长方形的面积
【解析】【解答】解：（10÷2）×（6÷2）
=5×3
=15（平方厘米）
故答案为：15。
【分析】长方形的面积=长×宽；其中，长=原来的长÷2，宽=原来的宽÷2。
11．【答案】B
【知识点】百分数的其他应用；比的化简与求值
【解析】【解答】解：甲数×25%=乙数×=1，则甲数=4，乙数=，甲数和乙数的比是4：=8：5。
故答案为：B。
【分析】根据分数乘法的意义得到甲数×25%=乙数×，假设它们的值都是1，则分别计算出两个数，写出两个数的比并化成最简整数比即可。
12．【答案】A
【知识点】成正比例的量及其意义；成反比例的量及其意义
【解析】【解答】解：A：钱数÷足球的个数=单价（一定），买足球的个数和钱数成正比例；
B：运送一批货物，运走的吨数和剩下的吨数不成比例；
C：分母×分数值=分子（一定），所以分母和分数值成反比例；
D：底面周长×高=侧面积，则底面半径×高=侧面积÷（2π）（一定），所以成反比例。
故答案为：A。
【分析】根据数量关系判断相关联的两个量的商一定还是乘积一定，如果商一定就成正比例；如果乘积一定就成反比例；否则不成比例。
13．【答案】C
【知识点】圆柱的侧面积、表面积
【解析】【解答】解：3.14×5×2×2
=3.14×20
=62.8（cm2）
故答案为：C。
【分析】圆柱的侧面积=底面周长×高，所以用圆柱的底面周长乘高增加的高度即可求出侧面积增加的部分。
14．【答案】D
【知识点】圆柱的体积（容积）；圆锥的体积（容积）
【解析】【解答】解：A：等底等高的圆柱的体积和正方体的体积相等。此选项错误；
B：等底等高的圆柱和正方体的表面积不相同。此选项错误；
C：等底等高的圆柱的体积是圆锥的。此选项错误；
D：等底等高的圆锥的体积是正方体的。此选项正确。
故答案为：D。
【分析】正方体、圆柱体的体积都可以用底面积乘高来计算，所以等底等高的正方体和圆柱的体积相等。圆锥的体积=底面积×高×，所以等底等高的圆锥的体积是正方体体积和圆柱体积的。
15．【答案】C
【知识点】比例的基本性质
【解析】【解答】解：A、B、D，根据比例的基本性质都能得到ab＝cd，能组成比例；
C：能得到ad=bc，所以不能组成比例。
故答案为：C。
【分析】比例的基本性质：在比例里，两个内项的积等于两个外项的积。根据比例的基本性质逐个判断并选择即可。
16．【答案】C
【知识点】将简单图形平移或旋转一定的度数
【解析】【解答】解：这个图形绕点O逆时针旋转90°得到的图形是。
故答案为：C。
【分析】绕一个图形上一点逆时针旋转一定的度数，先把这个点连接的边逆时针旋转相同的度数，然后把剩下的部分连接起来即可。
17．【答案】B
【知识点】圆锥的体积（容积）
【解析】【解答】解：两个圆锥的高相等，底面半径的比是3：2，底面积的比是9：4，则体积比为9：4。
故答案为：B。
【分析】根据圆面积公式可知，底面积的比是底面半径平方的比。圆锥的高不变，体积的比与底面积的比相同。
18．【答案】（1） 3x﹣0.15×12＝9
解：3x﹣1.8+1.8＝9+1.8
3x÷3＝10.8÷3
x＝3.6
（2） ：x=：
解： x＝ ×
x× ＝ ×
x＝
（3）
解：6x＝3×2.5
6x÷6＝7.5÷6
x＝1.25
【知识点】应用比例的基本性质解比例
【解析】【分析】解方程要掌握等式的性质，即等式两边同时加上或减去同一个数，左右两边仍然相等；等式两边同时乘或除以同一个不是0的数，等式两边仍然相等。解比例时根据比例的基本性质把比例写成两个內项积等于两个外项积的形式，然后根据等式的性质求出未知数的值。
19．【答案】解：3.14×5×20+3.14×（5÷2）2×2
＝314+3.14×6.25×2
＝314+39.25
＝353.25（平方分米）
答：这个圆柱的表面积是353.25平方分米。
【知识点】圆柱的侧面积、表面积
【解析】【分析】圆柱的表面积=侧面积+2个底面积，圆柱的侧面积=底面周长×高，根据圆面积公式求出2个底面积，再加上侧面积即可求出表面积。
20．【答案】解：3.14×（8÷2）2×10+3.14×（8÷2）2×9×
＝3.14×（160+48）
＝653.12（立方厘米）
答：它的体积是653.12立方厘米。
【知识点】圆柱的体积（容积）；圆锥的体积（容积）；组合体的体积的巧算
【解析】【分析】圆柱的体积=底面积×高，圆锥的体积=底面积×高×，根据公式分别计算，把圆锥和圆柱的体积相加求出组合图形的体积。
21．【答案】（1）解：
（2）解：
（3）解：
【知识点】图形的缩放；补全轴对称图形；作平移后的图形；作旋转后的图形
【解析】【分析】（1）轴对称图形对应点到对称轴的距离相等，所以先确定对应点的位置，再画出轴对称图形的另一半；
（2）按2：1放大后的平行四边形底是6格，高是4格，注意高的位置，然后画出放大后的平行四边形；
（3）根据旋转中心、方向和度数确定旋转后的图形，然后根据平移的方向和格数确定平移后图形的位置并画出图形即可。
22．【答案】解：设需要方砖x块。
2×2×90＝3×3×x
9x＝360
x＝40
答：需要方砖40块。
【知识点】反比例应用题
【解析】【分析】书房的面积不变，每块方砖的面积与需要方砖的块数成反比例，先设出未知数，然后根据总面积不变列出比例解答即可。
23．【答案】解：80÷2＝40（米）
40÷（3+2）
＝40÷5
＝8（米）
8×3＝24（米）
8×2＝16（米）
24米＝2400厘米
2400× ＝2.4（厘米）
16米＝1600厘米
1600× ＝1.6（厘米）
答：长画在图上是2.4厘米，宽画在图上是1.6厘米。
【知识点】应用比例尺求图上距离或实际距离
【解析】【分析】用长方形的周长除以2求出一组长与宽的和，然后把长与宽的和按照3：2的比分配后分别求出长和宽。然后把长和宽都换算成厘米，用实际距离乘比例尺分别求出图上的长和宽即可。
24．【答案】解：24﹣20＝4（厘米）
3.14×（10÷2）2×4
＝3.14×100
＝314（立方厘米）
答：这块石头的体积是314立方厘米。
【知识点】圆柱的体积（容积）；不规则物体的体积算法
【解析】【分析】水面上升部分水的体积就是石头的体积，所以用圆柱的底面积乘水面上升的高度即可求出石头的体积。
25．【答案】解：2×3＝6（米）
4厘米＝0.04米
3.14×22×6× ÷（8×0.04）
＝3.14×4×6× ÷0.32
＝25.12÷0.32
＝78.5（米）
答：能铺78.5米。
【知识点】圆锥的体积（容积）
【解析】【分析】高与底面半径的比是3：1，那么高是底面半径的3倍，所以用底面半径乘3即可求出高。根据圆锥的体积公式计算出沙堆的体积。用沙堆的体积除以路面宽与厚度的积即可求出能铺的长度。注意换算单位。圆锥的体积=底面积×高×。
26．【答案】（1）解：
（2）解：因为路程÷时间＝速度（一定），可知速度没有变，路程与时间之间成正比例关系。
（3）解：4分半＝4.5分
7×4.5＝31.5（千米）
答：列车行驶4分半时，所行路程是31.5千米。
【知识点】成正比例的量及其意义
【解析】【分析】（1）根据表格中数据可知，每分钟能行驶7千米，然后把统计表补充完整；在图像中依次找出各个对应点，然后顺次连接成正比例图像；
（2）路程和时间的商一定，所以路程和时间成正比例关系；
（3）可以用速度乘行驶的时间求出行驶的路程。题号
一
二
三
四
五
总分
评分
阅卷人
一、填空题
得分
阅卷人
二、选择题
得分
阅卷人
三、计算题
得分
阅卷人
四、画一画
得分
阅卷人
五、解决问题
得分
时间/分
1
2
3
4
5
6
7
8
9
路程/千米
7
14
21
28
35




时间/分
1
2
3
4
5
6
7
8
9
路程/千米
7
14
21
28
35
42
49
56
63