
还剩7页未读,
继续阅读
所属成套资源:新人教a版数学必修第二册PPT课件+教案+导学案+分层作业(原卷+解析卷)(含章末总结和知识点)
成套系列资料,整套一键下载
高中数学人教A版 (2019)必修 第二册10.1 随机事件与概率精品教案
展开这是一份高中数学人教A版 (2019)必修 第二册10.1 随机事件与概率精品教案,共10页。教案主要包含了类题通法,巩固练习1,巩固练习2,设计意图等内容,欢迎下载使用。
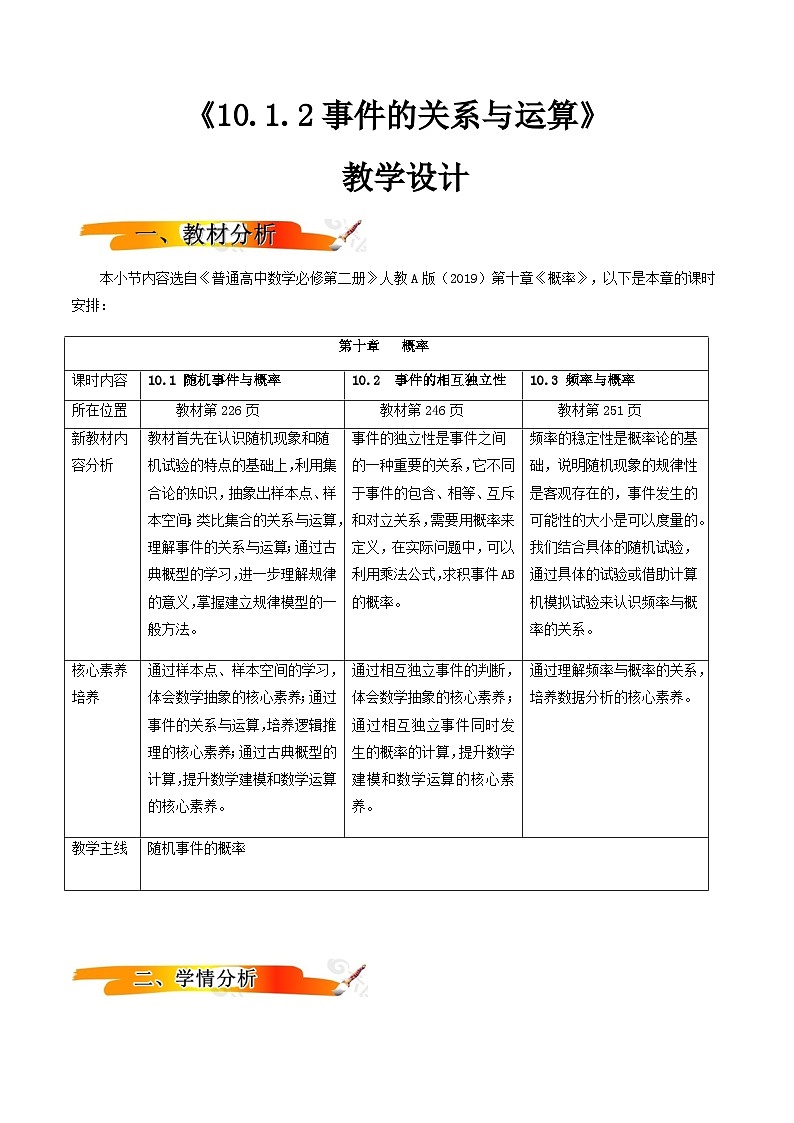
本小节内容选自《普通高中数学必修第二册》人教A版(2019)第十章《概率》,以下是本章的课时安排:
本节课是对上方一节课内容的延伸,继续研究事件之间的关系和运算
1.理解事件的关系与运算,培养学生数学抽象的核心素养;
2.通过事件之间的运算,理解互斥事件和对立事件的概念,培养学生数学抽象的核心素养。
1.重点:了解随机事件的并、交与互斥的含义,会进行简单的随机事件的运算.
2.难点:判断事件的关系、进行事件的运算。
(一)新知导入
在掷骰子试验中,定义如下事件:C1={出现1点};C2={出现2点};C3={出现3点};C4={出现4点};C5={出现5点};C6={出现6点};D1={出现的点数不大于1};D2={出现的点数不大于3};D3={出现的点数不大于5};E={出现的点数小于5},F={出现的点数大于4},G={出现的点数为偶数},H={出现的点数为奇数}.
【问题 】在上述事件中,(1)事件C1与事件C2的并事件是什么?(2)事件D2与事件G及事件C2间有什么关系?(3)事件C1与事件C2间有什么关系?(4)事件E与事件F间有什么关系?
【提示】(1)C1∪C2={出现1点或2点};(2)D2∩G=C2;(3)事件C1与事件C2互斥;(4)事件E与事件F对立.
(二)事件的关系和运算
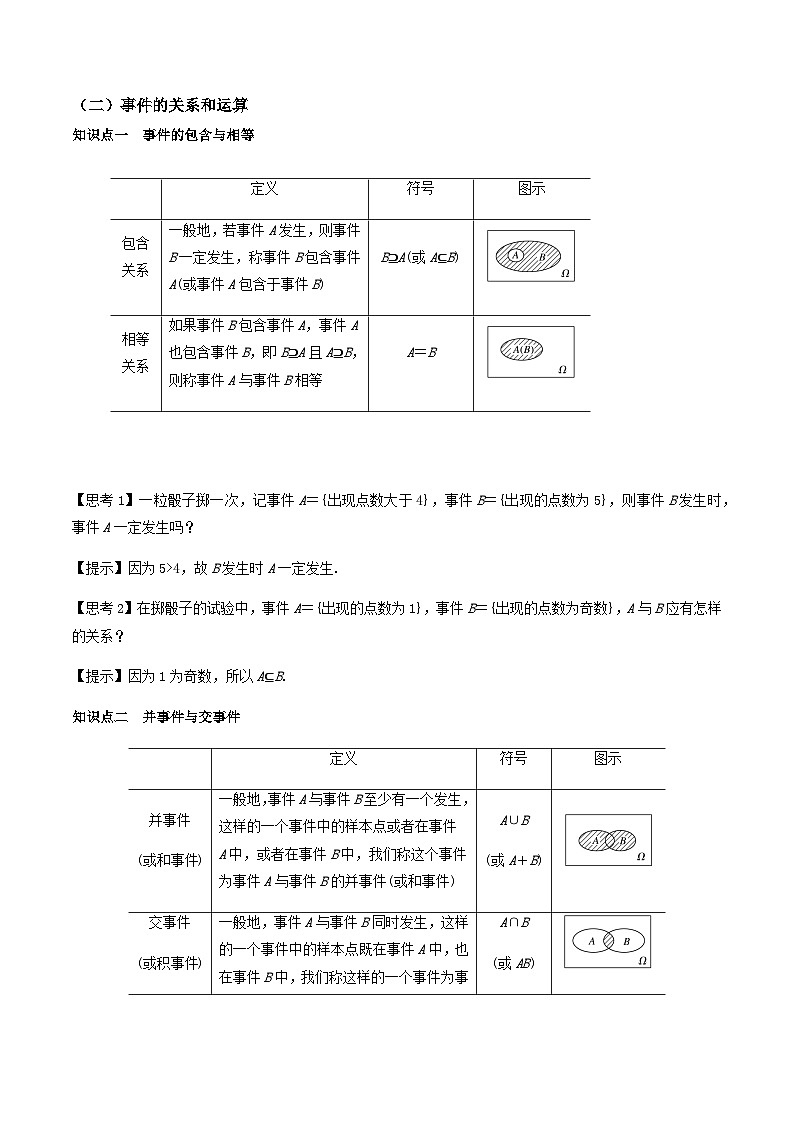
知识点一 事件的包含与相等
【思考1】一粒骰子掷一次,记事件A={出现点数大于4},事件B={出现的点数为5},则事件B发生时,事件A一定发生吗?
【提示】因为5>4,故B发生时A一定发生.
【思考2】在掷骰子的试验中,事件A={出现的点数为1},事件B={出现的点数为奇数},A与B应有怎样的关系?
【提示】因为1为奇数,所以A⊆B.
知识点二 并事件与交事件
知识点三 互斥事件与对立事件
【思考】判断两个事件是对立事件的条件是什么?
【提示】 ①看是否是互斥事件,②看两个事件是否必有一个发生.若满足这两个条件,则是对立事件;否则不是.
【辩一辩】从装有2个红球和2个黑球的口袋中任取2个球,判断下列事件哪些是互斥而不对立的两事件.
(1)“至少有1个黑球”和“都是黑球”.(×)
(2)“至少有1个黑球”和“至少有1个红球”.(×)
(3)“恰有1个黑球”和“恰有2个红球”.(√)
(4)“至少有1个黑球”和“都是红球”(×)
(三)典型例题
1.事件关系的判断
例1. 从40张扑克牌(红桃、黑桃、方块、梅花,点数从1~10各4张)中,任取一张.
(1)“抽出红桃”与“抽出黑桃”;
(2)“抽出红色牌”与“抽出黑色牌”;
(3)“抽出的牌点数为5的倍数”与“抽出的牌点数大于9”.
判断上面给出的每对事件是否为互斥事件,是否为对立事件,并说明理由.
【解】(1)是互斥事件,不是对立事件.
理由是:从40张扑克牌中任意抽取1张,“抽出红桃”和“抽出黑桃”是不可能同时发生的,所以是互斥事件.同时,不能保证其中必有一个发生,这是由于还可能抽出“方块”或者“梅花”,因此,二者不是对立事件.
(2)既是互斥事件,又是对立事件.
理由是:从40张扑克牌中,任意抽取1张,“抽出红色牌”与“抽出黑色牌”,两个事件不可能同时发生,但其中必有一个发生,所以它们既是互斥事件,又是对立事件.
(3)不是互斥事件,当然不可能是对立事件.
理由是:从40张扑克牌中任意抽取1张,“抽出的牌点数为5的倍数”与“抽出的牌点数大于9”这两个事件可能同时发生,如抽得牌点数为10,因此,二者不是互斥事件,当然不可能是对立事件.
【类题通法】互斥事件与对立事件的判断方法
(1)利用基本概念:判断两个事件是否为互斥事件,注意看它们能否同时发生,若不同时发生,则这两个事件是互斥事件,若能同时发生,则这两个事件不是互斥事件.
(2)判断两个事件是否为对立事件,主要看是否同时满足两个条件:一是不能同时发生;二是必有一个发生,如果这两个条件同时成立,那么这两个事件就是对立事件,只要有一个条件不成立,那么这两个事件就不是对立事件.两个事件是对立事件的前提是互斥事件.
【巩固练习1】从一批产品(既有正品也有次品)中取出3件产品,设A={3件产品全不是次品},B={3件产品全是次品},C={3件产品不全是次品},则下列结论正确的是________(填写序号).
①A与B互斥;②B与C互斥;③A与C互斥;④A与B对立;⑤B与C对立.
【解析】 A={3件产品全不是次品},指的是3件产品全是正品,B={3件产品全是次品},C={3件产品不全是次品},它包括1件次品2件正品,2件次品1件正品,3件全是正品3个事件,由此知:A与B是互斥事件,但不对立;A与C是包含关系,不是互斥事件,更不是对立事件;B与C是互斥事件,也是对立事件.
所以正确结论的序号为①②⑤.
【答案】 ①②⑤
2.事件的运算
例2.盒子里有6个红球,4个白球,现从中任取3个球,设事件A={3个球中有1个红球2个白球},事件B={3个球中有2个红球1个白球},事件C={3个球中至少有1个红球},事件D={3个球中既有红球又有白球}.
求:(1)事件D与A,B是什么样的运算关系?
(2)事件C与A的交事件是什么事件?
【解】(1)对于事件D,可能的结果为:1个红球,2个白球或2个红球,1个白球,故D=A∪B.
(2)对于事件C,可能的结果为1个红球,2个白球或2个红球,1个白球或3个均为红球,故C∩A=A.
【类题通法】事件的混合运算的方法
(1)利用事件间运算的定义.列出同一条件下的试验的所有样本点,分析并利用这些样本点进行事件间的运算.
(2)利用Venn图.借助集合间运算的思想,分析同一条件下的试验所有样本点,把这些样本点在图中列出,进行运算.
【巩固练习2】掷一枚骰子,下列事件:
A={出现奇数点},B={出现偶数点},C={点数小于3},D={点数大于2},E={点数是3的倍数}.
求:(1)A∩B,BC;
(2)A∪B,B+C;
(3)记eq \x\t(H)是事件H的对立事件,求eq \x\t(D),eq \x\t(A)C,eq \x\t(B)∪C,eq \x\t(D)+eq \x\t(E).
【解】(1)A∩B=∅,BC={出现2点}.
(2)A∪B={出现1,2,3,4,5或6点},B+C={出现1,2,4或6点}.
(3)eq \x\t(D)={点数小于或等于2}={出现1或2点},
eq \x\t(A)C=BC={出现2点},
eq \x\t(B)∪C=A∪C={出现1,2,3或5点},
eq \x\t(D)+eq \x\t(E)={出现1,2,4或5点}.
(四)操作演练 素养提升
1、把红、蓝、黑、白4张纸牌随机分给甲、乙、丙、丁四人,每人分得一张,那么事件“甲分得红牌”与事件“乙分得红牌”是( )
A.对立事件 B.互斥但不对立事件 C.必然事件 D.不可能事件
2、掷一枚骰子,设事件A={出现的点数不大于3},B={出现的点数为偶数},则事件A与事件B的关系是( )
A.A⊆B B.A∩B={出现的点数为2}
C.事件A与B互斥 D.事件A与B是对立事件
3、对空中飞行的飞机连续射击两次,每次发射一枚炮弹,设A={两次都击中飞机},B={两次都没击中飞机},C={恰有一炮弹击中飞机},D={至少有一炮弹击中飞机},下列关系不正确的是( )
A.A⊆D B.B∩D=∅ C.A∪C=D D.A∪B=B∪D
4、设A,B,C为三个事件,则A+B+C表示的意义是________.
【答案】1.B 2.B 3.D 4.事件A,B,C至少有一个发生
【设计意图】通过练习巩固本节所学知识,通过学生解决问题的能力,感悟其中蕴含的数学思想,增强学生的应用意识。
(五)课堂小结,反思感悟
1.知识总结:
2.学生反思:
(1)通过这节课,你学到了什么知识?
(2)在解决问题时,用到了哪些数学思想?
【设计意图】
通过总结,让学生进一步巩固本节所学内容,提高概括能力,提高学生的数学运算能力和逻辑推理能力。
完成教材:第233页 练习 第1,2题
第243页 习题10.1 第3,4题
第十章 概率
课时内容
10.1 随机事件与概率
10.2 事件的相互独立性
10.3 频率与概率
所在位置
教材第226页
教材第246页
教材第251页
新教材内容分析
教材首先在认识随机现象和随机试验的特点的基础上,利用集合论的知识,抽象出样本点、样本空间;类比集合的关系与运算,理解事件的关系与运算;通过古典概型的学习,进一步理解规律的意义,掌握建立规律模型的一般方法。
事件的独立性是事件之间的一种重要的关系,它不同于事件的包含、相等、互斥和对立关系,需要用概率来定义,在实际问题中,可以利用乘法公式,求积事件AB的概率。
频率的稳定性是概率论的基础,说明随机现象的规律性是客观存在的,事件发生的可能性的大小是可以度量的。我们结合具体的随机试验,通过具体的试验或借助计算机模拟试验来认识频率与概率的关系。
核心素养培养
通过样本点、样本空间的学习,体会数学抽象的核心素养;通过事件的关系与运算,培养逻辑推理的核心素养;通过古典概型的计算,提升数学建模和数学运算的核心素养。
通过相互独立事件的判断,体会数学抽象的核心素养;通过相互独立事件同时发生的概率的计算,提升数学建模和数学运算的核心素养。
通过理解频率与概率的关系,培养数据分析的核心素养。
教学主线
随机事件的概率
定义
符号
图示
包含关系
一般地,若事件A发生,则事件B一定发生,称事件B包含事件A(或事件A包含于事件B)
B⊇A(或A⊆B)
相等关系
如果事件B包含事件A,事件A也包含事件B,即B⊇A且A⊇B,则称事件A与事件B相等
A=B
定义
符号
图示
并事件
(或和事件)
一般地,事件A与事件B至少有一个发生,这样的一个事件中的样本点或者在事件A中,或者在事件B中,我们称这个事件为事件A与事件B的并事件(或和事件)
A∪B
(或A+B)
交事件
(或积事件)
一般地,事件A与事件B同时发生,这样的一个事件中的样本点既在事件A中,也在事件B中,我们称这样的一个事件为事件A与事件B的交事件(或积事件)
A∩B
(或AB)
定义
符号
图示
互斥事件
一般地,如果事件A与事件B不能同时发生,也就是说A∩B是一个不可能事件,即A∩B=∅,则称事件A与事件B互斥(或互不相容)
A∩B=∅
对立事件
一般地,如果事件A和事件B在任何一次试验中有且仅有一个发生,即A∪B=Ω,且A∩B=∅,那么称事件A与事件B互为对立,事件A的对立事件记为eq \x\t(A)
A∪B=Ω
A∩B=∅
相关教案
数学必修 第二册10.1 随机事件与概率教案:
这是一份数学必修 第二册10.1 随机事件与概率教案,共3页。
数学人教A版 (2019)10.1 随机事件与概率教案:
这是一份数学人教A版 (2019)10.1 随机事件与概率教案,共6页。
高中数学人教A版 (2019)必修 第二册10.1 随机事件与概率教案:
这是一份高中数学人教A版 (2019)必修 第二册10.1 随机事件与概率教案,共6页。









