第18讲 等腰三角形（3考点 26题型）（讲义）-2024年中考数学一轮复习讲义（全国通用）

这是一份第18讲 等腰三角形（3考点 26题型）（讲义）-2024年中考数学一轮复习讲义（全国通用），文件包含第18讲等腰三角形讲义原卷版docx、第18讲等腰三角形讲义解析版docx等2份学案配套教学资源，其中学案共158页， 欢迎下载使用。

2、学会运用数形结合思想。数形结合思想是指从几何直观的角度,利用几何图形的性质研究数量关系，寻求代数问题的解决方法（以形助数）。
3、要学会抢得分点。要将整道题目解题思路转化为得分点。
4、学会运用等价转换思想。将抽象的问题转化为具体的问题，将实际问题转化为数学问题。
5、学会运用分类讨论的思想。如果不注意对各种情况分类讨论，就有可能造成错解或漏解，纵观近几年的中考压轴题分类讨论思想解题已成为新的热点。
6、转化思想：体现在数学上也就是要把难转简，把不熟转熟，把未知转为已知的问题。
第18讲 等腰三角形
目 录
TOC \ "1-3" \n \h \z \u \l "_Tc156158026" \l "_Tc156054062" 一、考情分析
二、知识建构
\l "_Tc156158027" 考点一 等腰三角形的性质与判定
\l "_Tc156158028" 题型01 等腰三角形的定义
\l "_Tc156158029" 题型02 根据等边对等角求角度
\l "_Tc156158030" 题型03 利用等边对等角证明
\l "_Tc156158031" 题型04 根据三线合一求解
\l "_Tc156158032" 题型05 根据三线合一证明
\l "_Tc156158033" 题型06 格点图中画等腰三角形
\l "_Tc156158034" 题型07 根据等角对等边证明等腰三角形
\l "_Tc156158035" 题型08 根据等角对等边证明边相等
\l "_Tc156158036" 题型09 根据等角对等边求边长
\l "_Tc156158037" 题型10 求与图形中任意两点构成等腰三角形的点
\l "_Tc156158038" 题型11 等腰三角形性质与判定综合
\l "_Tc156158039" 题型12 等腰三角形有关的折叠问题
\l "_Tc156158040" 题型13 等腰三角形有关的规律探究问题
\l "_Tc156158041" 题型14 等腰三角形有关的新定义问题
\l "_Tc156158042" 题型15 等腰三角形有关的动点问题
\l "_Tc156158043" 题型16 探究等腰三角形中线段间存在的关系
\l "_Tc156158044" 考点二 等边三角形的性质与判定
\l "_Tc156158045" 题型01 利用等边三角形的性质求线段长
\l "_Tc156158046" 题型02 手拉手模型
\l "_Tc156158047" 题型03 等边三角形的判定
\l "_Tc156158048" 题型04 等边三角形与折叠问题
\l "_Tc156158049" 题型05 等边三角形有关的规律探究问题
\l "_Tc156158050" 题型06 等边三角形有关的新定义问题
\l "_Tc156158051" 题型07 利用等边三角形的性质与判定解决多结论问题
\l "_Tc156158052" 考点三 线段垂直平分线的性质与判定定理
\l "_Tc156158053" 题型01 利用垂直平分线的性质求解
\l "_Tc156158054" 题型02 线段垂直平分线的判定
\l "_Tc156158055" 题型03 线段垂直平分线的实际应用
考点一 等腰三角形的性质与判定
等腰三角形的概念：有两边相等的三角形角等腰三角形．
等腰三角形性质：
1）等腰三角形的两个底角相等（简称“等边对等角”）.
2）等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.（简称“三线合一”）.
等腰三角形的判定：如果一个三角形有两个角相等，那么这两个角所对的边也相等（简称“等角对等边”）.
1. 等腰三角形的边有腰、底之分,角有顶角、底角之分,若题目中的边没有明确是底还是腰,角没有明是顶角还是底角，需要分类讨论.
2. 顶角是直角的等腰三角形叫做等腰直角三角形，且它的两个底角都为45°.
3. 等腰三角形是轴对称图形，它有1条或3条对称轴．
4. 等腰三角形的底角只能为锐角，不能为钝角（或直角），但顶角可为钝角（或直角）．
5. 等腰三角形的三边关系：设腰长为a，底边长为b，则b26. 等腰三角形的三角关系：设顶角为顶角为∠A，底角为∠B、∠C，则∠A=180°-2∠B，∠B=∠C=1800−∠A2
7. 底角为顶角的2倍的等腰三角形非常特殊，其底角平分线将原等腰三角形分成两个等腰三角形．（即顶角36°，底角72°）.
8. 等腰三角形的判定定理是证明两条线段相等的重要依据，是把三角形中的角的相等关系转化为边的相等关系的重要依据．
题型01 等腰三角形的定义
【例1】（2023·山东济南·统考三模）已知m，n，5分别是等腰三角形（非等边三角形）三边的长，且m，n分别是关于x的一元二次方程x2−6x+k=0的两个根，则k的值等于（ ）
A．3B．5或9C．5D．9
【变式1-1】（2023·内蒙古鄂尔多斯·三模）腰长为5，一边上的高为4的等腰三角形的底边长为（ ）
A．6或45B．6或45或25C．45或25D．6或25
【变式1-2】（2023·湖南邵阳·统考二模）已知等腰三角形的三边x、y、z满足x−42+y−2+z−a=0，则a的值是（ ）
A．2B．3C．4D．2或4
【变式1-3】（2023·河南安阳·统考一模）已知等腰△ABC的边是方程x2−7x+10=0的根，则△ABC的周长为（ ）
A．9B．9或12C．6或15D．6或12或15
【变式1-4】（2023·黑龙江佳木斯·统考三模）已知△ABC是以AB为一腰的等腰三角形，AB=5，AC边上的高为4，则△ABC的底边长为 ．
题型02 根据等边对等角求角度
【例2】（2023·湖北襄阳·统考模拟预测）等腰三角形腰长为8，面积为16，则底角的度数为 ．
【变式2-1】（2023·安徽滁州·校考一模）如图，△ABC中，AB=AC，CD⊥AB于点D，若∠A=40°，则有（ ）

A．∠1=50°B．∠1=40°C．∠1=35°D．∠1=20°
【变式2-2】．（2023·辽宁丹东·校考二模）如图，A，B两点分别在直线l1，l2上，且l1∥l2，BA=BC，BC⊥l2，若∠1=116°，则∠CAB的度数等于（ ）

A．20°B．22°C．24°D．26°
【变式2-3】（2023·广东河源·统考一模）如图，在△ABC中，AB=AC，∠A=40°，CE平分△ABC的外角∠ACD，则∠1= ．
【变式2-4】（2023·江西吉安·校考模拟预测）如图，在△ABC中，AC=BC，AE⊥BC．垂足为E，点D在AE上，且CD平分∠ACB，若∠ABC=54°，则∠ADC的度数为 ．

【变式2-5】（2023·浙江金华·校考一模）等腰△ABC中，BD⊥AC，垂足为点D，且BD=12AC，则等腰△ABC底角的度数为 ．
题型03 利用等边对等角证明
【例3】（2023·浙江温州·统考二模）如图，在△ABC中，AB=AC，P为BC的中点，D，E分别为AB，AC上的点，且∠BDP=∠CEP．

(1)求证：△BDP≌△CEP．
(2)若PD⊥AB，∠A=110°，求∠EPC的度数．
【变式3-1】（2023·陕西西安·陕西师大附中校考模拟预测）如图，在四边形ABCD中，AD∥BC，∠ABC=∠BCD，连接AC，点M为线段AC上一点，连接BM，若AC=BC，AB=BM．求证：△ADC≌△CMB．

【变式3-2】（2023·黑龙江哈尔滨·哈尔滨市第十七中学校校考模拟预测）已知：▱ABCD中，DE=BC，BE=EF．

(1)求证：AF=DC；
(2)连接AE，当AE=AF时，在不添加任何辅助线和字母的情况下，请直接写出图中与∠B互补的角．
【变式3-3】（2023·江苏无锡·校考二模）如图，△ABC中，AB=AC，点D、E分别在AB、AC边上，∠EBC=∠DCB．

(1)求证：BE=CD；
(2)若AB=8，BC=5，当CD⊥AB时，求CE的长．
题型04 根据三线合一求解
【例4】（2023·辽宁·模拟预测）如图，线段AB=8，点P在线段AB上，且AP=5，分别以点A和点B为圆心，AP的长为半径作孤，两弧相交于点C和点D，连接AC，BC，AD，BD，则点C到边AD的距离是（ ）

A．245B．485C．4D．3
【变式4-1】（2023·陕西西安·校考模拟预测）图1为红斑钟螺，壳型为圆锥形．多分布在菲律宾、以及我国台湾垦丁等区域．现有一个“钟螺”小摆件，可近似看成圆锥形，图2为其主视图，其中AB=13cm，摆件的高度为12cm．现要在AB上选取一个位置P安装挂钩，在该点与C之间布设导线，线路上安装微型小彩灯，若挂钩以及导线连接处等长度损耗忽略不计，则最短线路，即CP的最小值为（ ）

A．10cmB．12013cmC．6013cmD．63cm
【变式4-2】（2023·吉林松原·校联考二模）如图，在△ABC中，AB=AC，边BC在x轴上，且点B−1,0，点A2,4，则△AOC的面积为（ ）

A．5B．8C．10D．20
【变式4-3】（2023·陕西西安·校考二模）如图，等腰△AOB在平面直角坐标系中，点B的坐标为6，0，OA=AB=5，点A在反比例函数y=kx（k≠0，x>0）的图象上，则k的值为 ．

【变式4-4】（2023·河北·统考模拟预测）如图，点D,C,E在直线l上，点A,B在l的同侧，AC⊥BC，若AD=AC=BC=BE=5,CD=6，则CE的长为 ．

题型05 根据三线合一证明
【例5】（2023·陕西榆林·校考模拟预测）如图，在△ABC中，AB=AC，D是边BC的中点，一个圆过点A，交边AB于点E，且与BC相切于点D，则该圆的圆心是（ ）
A．线段AE的垂直平分线与线段AC的垂直平分线的交点
B．线段AB的垂直平分线与线段AC的垂直平分线的交点
C．线段AE的垂直平分线与线段BC的垂直平分线的交点
D．线段AB的垂直平分线与线段BC的垂直平分线的交点
【变式5-1】（2023·山东青岛·统考一模）如图，在▱ABCD中，AC，BD交于点O，点E，F分别是AO，CO的中点．
(1)求证：DE=BF；
(2)请从以下三个条件：①AC=2BD；②∠BAC=∠DAC；③AB=AD中，选择一个合适的作为已知条件，使四边形DEBF为菱形．
你选择添加的条件是：______（填写序号）；添加条件后，请证明四边形DEBF为菱形．
【变式5-2】（2023·广西河池·校考一模）如图，在△ABC中，AB=AC，点D是边BC的中点．以BD为直径作圆O，交边AB于点P，连接PC，交AD于点E．
(1)求证：AD是圆O的切线．
(2)若PC是圆O的切线，BC=4，求PE的长．
【变式5-3】（2023·贵州黔东南·统考三模）（1）如图，直线AB经过⊙O上一点C，连接OA,OB，从以下三个信息中选择两个作为条件，剩余的一个作为结论组成一个真命题，并写出你的证明过程．①OA=OB；②CA=CB；③AB是⊙O的切线．你选择的条件是____________，结论是______（填序号）；
（2）在（1）的条件下，若∠AOB=90°，OA=42，求图中阴影部分的面积．
题型06 格点图中画等腰三角形
【例6】（2023·江苏扬州·统考一模）如图，在6×6的正方形网格图形ABCD中，每个小正方形的边长为1，M、N分别是AB、BC上的格点．若点P是这个网格图形中的格点，连接PM、PN，则满足∠MPN=45°的点P有（ ）个
A．3B．4C．5D．6
【变式6-1】（2023·广西玉林·统考一模）如图，在由边长相同的7个正六边形组成的网格中，点A，B在格点上．再选择一个格点C，使△ABC是以AB为腰的等腰三角形，符合点C条件的格点个数是( )

A．1B．2C．3D．4
【变式6-2】（2023·黑龙江哈尔滨·哈尔滨德强学校校考模拟预测）图1、图2是两张形状、大小完全相同的方格纸，方格纸中的每个小正方形的边长均为1

(1)在图1中画一个腰长为5，面积为10的等腰三角形ABC，（点A、B、C在小正方形的顶点上）．
(2)在图2中画出一个腰长为10的等腰三角形DEF（点D、E、F在小正方形的顶点上），并直接写出等腰三角形DEF的底角的正切值为__________．
【变式6-3】（2023·浙江丽水·统考二模）如图，是由边长为1的小等边三角形构成的网格，每个小等边三角形的顶点叫作格点．线段AB的端点均在网格上，分别按要求作图，每小题各画出一个即可．

(1)在图1中画出以AB为边的平行四边形ABCD，且点C，D在格点上；
(2)在图2中画出等腰三角形ABE，且点E在格点上；
(3)在图3中画出直角三角形ABF，且点F在格点上．
题型07 根据等角对等边证明等腰三角形
【例7】（2023·湖北武汉·校联考模拟预测）如图，D，E是△ABC边上的点，ED∥BC，BE平分∠ABC．

(1)求证：BD=DE；
(2)若BD:BC=2:3．直接写出S△ADE:S△EDC的值．
【变式7-1】（2023·江苏常州·统考二模）如图，已知△ABC．

(1)在图中用直尺和圆规作△ABC的角平分线BD，作∠ADE，使得∠ADE=∠C，射线DE交AB于点E（不写作法，保留作图痕迹）；
(2)在（1）的条件下，判断△BDE的形状，并证明你的结论．
【变式7-2】（2023·山东潍坊·统考模拟预测）如图，AB是⊙O的直径，D是AB上的一点，C是⊙O上的一点，过点D作AB的垂线，与过点C的切线相交于点P，PD与AC相交于点E．
（1）求证：△PCE是等腰三角形；
（2）连接BC，若AD=OD，AE=258，BC=6，求PC的长．
题型08 根据等角对等边证明边相等
【例8】（2023·陕西西安·交大附中分校校考模拟预测）如图，在平行四边形ABCD中，AB=6，AD=9，∠BAD的平分线交BC于点E，交DC的延长线于点F则CF的长为（ ）

A．2B．3C．3.5D．4
【变式8-1】（2023·江苏苏州·统考二模）如图锐角△ABC中，AB=4，BC=6，∠A=2∠C，则AC的值为 ．

【变式8-2】（2023·浙江·统考二模）如图，在△ABC中，点D，E分别在边AB，AC上，DE∥BC，EB平分∠DEC．

(1)求证：BC=CE；
(2)若CE=AB，EA=EB，求∠C的度数．
【变式8-3】（2023·湖北武汉·统考二模）如图，AB∥CD，AD∥BC，∠ABC的平分线交AD于点E，交CD的延长线于点F．

(1)求证：DE=DF；
(2)若∠C=120°，直接写出∠1的度数．
题型09 根据等角对等边求边长
【例9】（2023·福建福州·福建省福州第十九中学校考模拟预测）如图，正方形ABCD的边长为2，点F为对角线AC上一点，当∠CBF=22.5°时，则AF的长是（ ）

A．22−2B．116C．2D．5
【变式9-1】（2023·陕西西安·校考模拟预测）如图，在△ABC中，∠B=45°，AD是△ABC的角平分线，DE⊥AC，垂足为点E.若DE=2，则BD的长为（ ）

A．4B．23C．2D．22
【变式9-2】（2023·河北石家庄·石家庄市第四十中学校考二模）如图，在▱ABCD中，AB=6，BC=8，以点C为圆心，适当长为半径作弧，分别交BC，CD于M，N两点，分别以M，N为圆心，以大于12MN的长为半径作弧，两弧在∠BCD的内部交于点P，射线CP交AD于点E，交BA的延长线于点F，则AF的长是（ ）

A．1B．2C．3D．4
题型10 求与图形中任意两点构成等腰三角形的点
【例10】（2020·安徽淮北·统考一模）如图，在矩形ABCD中， AB=4,BC=6,点E是AD的中点，点F在DC上，且CF=1,若在此矩形上存在一点P，使得△PEF是等腰三角形，则点P的个数是（ ）

A．3B．4C．5D．6
【变式10-1】（2018·江苏常州·统考一模）已知直线y=−3x+3与坐标轴分别交于点A，B，点P在抛物线y=−x−32+4上，能使△ABP为等腰三角形的点P的个数有( )
A．8个B．4个C．5个D．6个
【变式10-2】．（2023·广东河源·统考一模）如图，在3×3的网格中，每个网格线的交点称为格点．已知图中A，B两个格点，请在图中再寻找另一个格点C，使△ABC成为等腰三角形，则满足条件的点C有（ ）个．
A．6B．8C．10D．12
题型11 等腰三角形性质与判定综合
【例11】（2023·北京顺义·统考二模）如图，在△ABC中，AD，BD分别是∠BAC，∠ABC的平分线，过点D作EF∥AB，分别交AC，BC于点E，F．若AE=4，BF=6，则EF的长为 ．

【变式11-1】（2020·江苏泰州·统考一模）已知点A(2，m)，点P在y轴上，且△POA为等腰三角形，若符合条件的点P恰好有2个，则m= ．
【变式11-2】（2023·湖南邵阳·统考一模）如图，已知AB=63，点C在线段AB上，△ACD是底边长为6的等腰三角形且∠ADC=120°，以CD为边在CD的右侧作矩形CDEF，连接DF，点M是DF的中点，连接MB，则线段MB的最小值为 ．
【变式11-3】（2023·湖南娄底·统考一模）如图，函数y=kxx>0的图象过点An,2和B85,2n−3两点．

(1)求n和k的值；
(2)点C是双曲线上介于点A和点B之间的一个动点，若S△AOC=6，求C点的坐标；
(3)过C点作DE∥OA，交x轴于点D，交y轴于点E，第二象限内是否存在点F，使得△DEF是以DE为腰的等腰直角三角形?若存在，请求出点F的坐标；若不存在，请说明理由．
题型12 等腰三角形有关的折叠问题
【例12】（2023·辽宁·模拟预测）【问题初探】
（1）在数学活动课上，李老师给出如下问题：如图1，在△ACD中，∠D=2∠C，AB⊥CD，垂足为B，且BC>AB．求证：BC=AD+BD．

①如图2，小鹏同学从结论的角度出发给出如下解题思路：在BC上截取BE=BD，连接AE，将线段BC与AD，BD之间的数量关系转化为AD与CE之间的数量关系．

②如图3，小亮同学从∠D=2∠C这个条件出发给出另一种解题思路：作AC的垂直平分线，分别与AC，CD交于F，E两点，连接AE，将∠D=2∠C转化为∠D与∠BEA之间的数量关系．

请你选择一名同学的解题思路，写出证明过程．
【类此分析】
（2）李老师发现之前两名同学都运用了转化思想，将证明三条线段的关系转化为证明两条线段的关系；为了帮助学生更好地感悟转化思想，李老师将图1进行变换并提出了下面问题，请你解答．
如图4，在Rt△ABC中，∠ABC=90°，过点A作AD∥BC（点D与点C在AB同侧），若∠ADB=2∠C．求证：BC=AD+BD．

【学以致用】
（3）如图5，在四边形ABCD中，AD=1003,CD=1213,sinD=35,∠BCD=∠BAD,∠ABC=3∠ADC，求四边形ABCD的面积．

【变式12-1】（2023·福建南平·统考二模）在等腰三角形ABC中，AB=AC，△DEC是由△ABC绕点C按顺时针方向旋转α角0<α<180°得到，且点A的对应点D恰好落在直线BC上，如图1．
(1)判断直线CE与直线AB的位置关系，并证明；
(2)当∠ADC=2∠BAC时，求∠BAC的大小；
(3)如图2，点F为线段AD的中点，点G在线段AB上且AG=AF，当点E在线段AD上时，求证：AB=AE+2BG．
【变式12-2】（2023·黑龙江齐齐哈尔·模拟预测）如图1，已知三角形纸片ABC，AB=AC，∠A=50°，将其折叠，如图2，使点A与点B重合，折痕为ED，点E，D分别在AB，AC上，那么∠DBC的度数为（ ）

A．10°B．15°C．20°D．30°
【变式12-3】（2023·河南南阳·统考模拟预测）如图，在矩形ABCD中，AB=8，BC=12，E为AD边的中点，连接BE，CE，点F，G分别是BE，BC边上的两个动点，连接FG，将△BFG沿FG折叠，使点B的对应点H恰好落在边EC上，若△CGH是以GH为腰的等腰三角形，则EH的长为 ．

【变式12-4】（2023·甘肃张掖·统考二模）（1）如图①，将矩形纸片ABCD沿对角线AC折叠，使点B落在点B'处，B'C与AD交于点E，求证：△AEC是等腰三角形；

（2）点O是矩形纸片ABCD对角线的交点，将该纸片沿过点O的线段EF折叠，使点A的对应点为A'，点B与点D重合，连接BF，求证：四边形FBED是菱形；
【变式12-5】（2023·河南洛阳·统考二模）综合与实践

(1)【操作发现】如图1，诸葛小组将正方形纸片ABCD沿过点A的直线折叠，使点B落在正方形内部的点M处，折痕为AE，再将纸片沿过点A的直线折叠，使AD与AM重合，折痕为AF，请写出图中的一个45°角：______．
(2)【拓展探究】如图2，孔明小组继续将正方形纸片沿EF继续折叠，点C的对应点恰好落在折痕AE上的点N处，连接NF交AM于点P．
①∠AEF=______度；
②若AB=3，求线段PM的长．
(3)【迁移应用】如图3，在矩形ABCD，点E，F分别在边BC、CD上，将矩形ABCD沿AE，AF折叠，点B落在点M处，点D落在点G处，点A，M，G恰好在同一直线上，若点F为CD的三等分点，AB=3，AD=5，请直接写出线段BE的长．
题型13 等腰三角形有关的规律探究问题
【例13】（2022·湖北荆门·校考模拟预测）如图，直角坐标系中，△A1A2A3，△A3A4A5，△A5A6A7…，是斜边在x轴上，斜边长分别为4，8，12，16，…的等腰直角三角形，若△A1A2A3的顶点坐标分别为A1(4,0)，A2(2,2)，A3(0,0)，则依图中所示规律，A2022的坐标为 ．
【变式13-1】（2022·四川成都·四川师范大学附属中学校考模拟预测）如图，在等腰RtΔABC中，已知∠ACB=90°，AC=BC=1，且AC边在直线a上．将ΔABC绕点A顺时针旋转到位置①可得到点P1，此时AP1=2；将位置①的三角形绕点P1顺时针旋转到位置②，可得到点P2，此时AP2=1+2；将位置②的三角形绕点P2顺时针旋转到位置③，可得到点P3，此时AP3=2+2；···，按此规律继续旋转，直至得到点P2022为止，则AP2022= ．
【变式13-2】（2022·山东潍坊·统考一模）如图，在平面直角坐标系xOy中，有一个等腰直角三角形AOB，∠OAB=90°，直角边AO在x轴上，且AO=1．将Rt△AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB，且A1O=2AO，再将Rt△A1OB1，绕原点O顺时针旋转90°得到等腰直角三角形A2OB2，且A2O=2A1O……，依此规律，得到等腰直角三角形A2021OB2021，则点B2022的坐标是 ．
【变式13-3】（2022·上海·校联考模拟预测）如图，在Rt△ABC中，∠ACB=90°，AC=BC=2，在Rt△ABC内部作正方形D1E1F1G1，其中点D1，E1分别在AC，BC边上，边F1G1在BC上，它的面积记作S1；按同样的方法在△CD1E1内部作正方形D2E2F2G2，它的面积记作S2，S2= ，…，照此规律作下去，正方形DnEnFnGn的面积Sn= ．
题型14 等腰三角形有关的新定义问题
【例14】（2023·江苏扬州·统考二模）给出一个新定义：有两个等腰三角形，如果它们的顶角相等、顶角顶点互相重合且其中一个等腰三角形的一个底角顶点在另一个等腰三角形的底边上，那么这两个等腰三角形互为“友好三角形”．

(1)如图①，△ABC和△ADE互为“友好三角形”，点D是BC边上一点（异于B点），AB=AC，AD=AE，∠BAC=∠DAE=m°，连接CE，则CE______BD（填“<”或“=”或“>”），∠BCE=______°（用含m的代数式表示）．
(2)如图②，△ABC和△ADE互为“友好三角形”，点D是BC边上一点，AB=AC，AD=AE，∠BAC=∠DAE=60°，M、N分别是底边BC、DE的中点，请探究MN与CE的数量关系，并说明理由．
(3)如图③，△ABC和△ADE互为“友好三角形”，点D是BC边上一动点，AB=AC，AD=AE，∠BAC=∠DAE=90°，BC=6，过D点作DF⊥AD，交直线CE于F点，若点D从B点运动到C点，直接写出F点运动的路径长．
【变式14-1】（2022·广东中山·统考三模）新定义：顶角相等且顶角顶点重合的两个等腰三角形互为“兄弟三角形”．
(1)如图1，△ABC和△ADE互为“兄弟三角形”，点A为重合的顶角顶点．求证：BD=CE．
(2)如图2，△ABC和△ADE互为“兄弟三角形”，点A为重合的顶角顶点，点D、E均在△ABC外，连接BD、CE交于点M，连接AM，求证：AM平分∠BME．
【变式14-2】（2023·广东阳江·统考三模）定义：△ABC中，∠A+2∠B=90°，则称△ABC为倍余三角形．

(1)下列说法正确的是 ．
①倍余三角形一定是钝角三角形；
②等腰三角形不可能是倍余三角形．
(2)如图1，△ABC内接于⊙O，点D在直径BC上(不与B，C重合)，满足AB=AD，求证：△ACD为倍余三角形；
(3)在（2）的条件下，
①如图1，连接AO，若△AOD也为倍余三角形，求∠C的度数；
②如图2，过点D作DE⊥BC交AC于点E，若△ABC面积为△ADE面积的7.5倍，求ADBC的值．
题型15 等腰三角形有关的动点问题
【例15】（2023·湖南郴州·统考二模）如图，等腰Rt△ABC中，D是AC上一动点，连接BD．将△BCD绕点B逆时针旋转90°得到△BAE，连接ED．若BC=5，则△AED周长最小值是 ．

【变式15-1】（2022·湖北咸宁·校考模拟预测）正方形ABCD中，E为对角线AC上的动点（不于B、C重合），连接BE，DE，作EF⊥BE交CD或其延长线于F，下列结论：①BE=DE；②△DEF为等腰三角形；③AE=CF；④CE
【变式15-2】（2023·吉林长春·校联考一模）（1）如图，△AOB和△COD是等腰直角三角形，∠AOB=∠COD=90，点C在OA上，点D在线段BO延长线上，连接AD，BC，则AD，BC的数量关系为______．
（2）如图2，将图1中的△COD绕点O顺时针旋转α0°<α<90°，第一问的结论是否仍然成立，证明你的结论，若不成立说明理由．
（3）如图3，若AB=8，点C是线段AB外一动点，AC=33，连接BC，若将CB绕点C逆时针旋转90°得到CD，连接AD，则AD的最大值是_____．
【变式15-3】（2022·湖北武汉·校考模拟预测）如图，在平面直角坐标系中，直线y=x+2分别交x轴、y轴于A、B两点，过点C2,2作x轴垂线，垂足为D，连BC．现有动点P、Q同时从A点出发，分别沿AB、AD向点B和点D运动（P、Q两点中有一点到达目标点，两者的运动随即停止），若点P的运动速度为2cm/s，点Q的运动速度为2cm/s．设运动的时间为ts．

(1)求A、B两点的坐标；
(2)当CQ∥AB时，求t的值；
(3)是否存在这样的时刻t，使△CPQ为等腰三角形？若存在，求出t的值；若不存在，请说明理由．
题型16 探究等腰三角形中线段间存在的关系
【例16】（2022·北京海淀·校考模拟预测）在△ABC中，∠BAC=90°，AB=AC，D是边AB上一点，点D与E关于直线AC对称，过点E作EF⊥CD交CD于G，交BC于F．
(1)补全图形；
(2)探究线段CD和EF的数量关系，并证明；
(3)直接写出线段BF的DE的数量关系______．
【变式16-1】（2023·江西南昌·校考二模）如图，在△ABC中，AB=AC，∠BAC=120°，点D在直线AC上，连接BD,将DB绕点D逆时针旋转120°，得到线段DE，连接BE，

(1)线段BC与AB的数量关系为 ；
拓展迁移
(2)当点D在线段AC上（点D不与点A，C重合）时，判断线段CE与AD之间的数量关系，并说明理由．
类比运用
(3)过点A作AN∥DE交BD于点N，若AD=2CD，请直接写出ANCE
【变式16-2】（2022·河北石家庄·校考模拟预测）如图，在△ABC中，AB=AC，∠BAC=90°，点D，E分别在AB，BC上，且∠EAD=∠EDA.延长DE，交AC的延长线于点F．

(1)求证：DE=EF；
(2)判断线段BD和CF的数量关系，并说明理由；
(3)若AB=AC=3，CF=1，求BE的长．
【变式16-3】（2022·北京海淀·校考模拟预测）如图，在△ABC中，∠ACB=90°，AC=BC，点D在线段AB上，连接CD，AE⊥CD于点E，以点A为圆心，CD长为半径画弧，交AE于点F，连接DF．
(1)依题意补全图形：
①设∠BCD=α，则∠DFA的度数为________________；（用含α的式子表示）
②求证：DF∥BC；
(2)探究DF、AF、BC之间的数量关系并证明．
考点二 等边三角形的性质与判定
等边三角形的概念：三条边都相等的三角形叫等边三角形，它是特殊的等腰三角形.
等边三角形的性质：1）等边三角形的三条边相等.
2）三个内角都相等，并且每个内角都是60°.
等边三角形的判定：1）三边相等或三个内角都相等的三角形是等边三角形.
1. 等边三角形具有等腰三角形的一切性质.
2. 等边三角形是轴对称图形，它有三条对称轴．
3．等边三角形的内心、外心、重心和垂心重合．
4. 在等腰三角形中，只要有一个角是60°，无论这个角是顶角还是底角，这个三角形就是等边三角形．
5. 等腰(等边)三角形顶角平分线平分底边并且垂直于底边，即等腰三角形的顶角平分线、底边上的中线、底边上的高重合．
6. 等边三角形面积的求解方法：S正三角形=34边长2
2）有一个角是60°的等腰三角形是等边三角形.
题型01 利用等边三角形的性质求线段长
【例1】（2022·黑龙江哈尔滨·哈尔滨市第六十九中学校校考二模）如图，△ABC是等边三角形，P是∠ABC的平分线BD上一点，PE⊥AB于点E，线段BP的垂直平分线交BC于点F，垂足为点Q．若BF=2，则PE的长为（ ）

A．2B．23C．3D．3
【变式1-1】（2022·湖北武汉·校考模拟预测）如图是由三个大小相同的正方形组成的“品”字型轴对称图案，测得顶点A，B之间的距离为5．现用一个等边三角形纸片将其完全覆盖，当此等边三角形面积最小时，则它的外接圆半径是（ ）

A．233+53B．233+83C．433+53D．433+83
【变式1-2】（2024·上海普陀·统考一模）已知点P为等边三角形ABC的重心，D为△ABC一边上的中点，如果这个等边三角形的边长为2，那么PD= ．
【变式1-3】（2022·湖北武汉·统考模拟预测）如图，△ABC中，∠ABC=30°，AB=33，D为BC边上一点，且BD=4，点E为AB边上一动点，△DEF为等边三角形，则线段AF的取值范围是 ．
题型02 手拉手模型
【例2】（2023·河南郑州·郑州市第八中学校考二模）由两个顶角相等且有公共顶角顶点的特殊多边形组成的图形，如果把它们的底角顶点连接起来，则在相对位置变化的过程中，始终存在一对全等三角形，我们把这种模型称为“手拉手模型”．

(1)【问题发现】
如图1所示，两个等腰直角三角形△ABC和△ADE中，AB=AC，AE=AD，∠BAC=∠DAE=90°，连接BD、CE，两线交于点P，BD和CE的数量关系是 ；BD和CE的位置关系是 ；
(2)【类比探究】
如图2所示，点P是线段AB上的动点，分别以AP、BP为边在AB的同侧作正方形APCD与正方形PBEF，连接DE分别交线段BC、PC于点M、N．
①求∠DMC的度数；
②连接AC交DE于点H，直接写出DHBC的值；
(3)【拓展延伸】
如图3所示，已知点C为线段AE上一点，AE=6，△ABC和△CDE为AE同侧的两个等边三角形，连接BE交CD于N，连接AD交BC于M，连接MN，直接写出线段MN的最大值．
【变式2-1】（2023·湖北武汉·模拟预测）两个顶角相等的等腰三角形，如果具有公共的顶角的顶点，并把它们的底角顶点连接起来，则形成一组全等的三角形，把具有这个规律的图形称为“手拉手”图形.
(1)问题发现：
如图1，若△ABC和△ADE是顶角相等的等腰三角形，BC，DE分别是底边.求证：BD=CE；
图1
(2)解决问题：如图2，若△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，点A，D，E在同一条直线上，CM为△DCE中DE边上的高，连接BE，请判断∠AEB的度数及线段CM，AE，BE之间的数量关系并说明理由.
图2
【变式2-2】（2021·广东中山·统考一模）△ABC和△ADE都是等边三角形．
(1)将△ADE绕点A旋转到图①的位置时，连接BD，CE并延长相交于点P（点P与点A重合），有PA+PB=PC（或PA+PC=PB）成立；请证明．
(2)将△ADE绕点A旋转到图②的位置时，连接BD，CE相交于点P，连接PA，猜想线段PA、PB、PC之间有怎样的数量关系？并加以证明；
(3)将△ADE绕点A旋转到图③的位置时，连接BD，CE相交于点P，连接PA，猜想线段PA、PB、PC之间有怎样的数量关系？直接写出结论，不需要证明．
题型03 等边三角形的判定
【例3】（2024·福建泉州·模拟预测）如图，点D在△ABC内部，△DAB逆时针旋转得到△EAC，请添加一个条件： ．使得△ADE是等边三角形．
【变式3-1】（2023·河北承德·校联考一模）如图，已知在⊙O中，弦AB垂直平分半径ON，NO的延长线交⊙O于P，连接AP，过点A，B的切线相交于点M．

(1)求证：△ABM是等边三角形；
(2)若⊙O的半径为2，求AP的长．
【变式3-2】（2023·广东佛山·校联考模拟预测）如图，在△ABC中，点O是AB边上的一点，⊙O与AC、BC分别相切于点A、E，AB与⊙O相交于点D，作▱ACEF，点F恰好为⊙O上一点．
(1)连接AE，求证：△ACE是等边三角形；
(2)若AC=6，求图中阴影部分面积．
题型04 等边三角形与折叠问题
【例4】（2023·河南信阳·校考三模）如图，在等边△ABC中，AB=2，点D在边AB上，点E是BC边上一动点，将∠B沿DE折叠，点B的对应点B'在AC边上，当△B'EC为直角三角形时，BE的长为 ．

【变式4-1】（2022·广东江门·统考一模）如图，在平行四边形ABCD中，将△ABD沿BD折叠后，点A恰好落在AD的延长线上的点E处．若∠C=60°，BC=4，则△ABE的周长为 ．

【变式4-2】（2023·浙江杭州·校联考一模）如图，点D是等边△ABC边BC上一点，将等边△ABC折叠，使点A与点D重合，折痕为EF（点E在边AB上）．（1）当FD⊥BC时，AE:EB= ；（2）当BD=2DC时，AE:EB= ．
题型05 等边三角形有关的规律探究问题
【例5】（2023·安徽滁州·校联考二模）如图所示，在平面直角坐标系中，△A1A2A3，△A3A4A5，△A5A6A7，⋯都是等边三角形，其边长依次为2，4，6，⋯其中点A1的坐标为2,0，点A2的坐标为1,−3，点A3的坐标为0,0，点A4的坐标为2,23，…，按此规律排下去，则点A100的坐标为（ ）

A．1,503B．1,513C．2,503D．2,513
【变式5-1】（2022·山东枣庄·校考一模）如图，在平面直角坐标系xy中，已知点A的坐标为0,2，以OA为边在右侧作等边三角形OAA1，过点A1作x轴的垂线，垂足为点O1：以O1A1为边在右侧作等边三角形O1A1A2，再过点A2作x轴的垂线，垂足为点O2；以O2A2为边在右侧作等边三角形O2A2A3,⋅⋅⋅，按此规律继续作下去，得到等边三角形O2022A2022A2023，则点A2023的纵坐标为 ．

【变式5-2】（2022·山东聊城·统考一模）如图，直线l1与直线l2所成的角∠B1OA1=30°，过点A1作A1B1⊥l1交直线l2于点B1，OB1=2，以A1B1为边在△OA1B1外侧作等边三角形A1B1C1，再过点C1作A2B2⊥l1，分别交直线l1和l2于A2，B2两点，以A2B2为边在△OA2B2外侧作等边三角形A2B2C2，…按此规律进行下去，则第2022个等边三角形A2022B2022C2022的周长为 ．
题型06 等边三角形有关的新定义问题
【例6】（2022·河南郑州·统考一模）定义：平面上一点P到图形的最短距离为d．如图，OP=3，等边三角形ABC的边长为23，点O为等边三角形的中心，当等边三角形ABC绕点O旋转时，d的取值范围是 ．
【变式6-1】（2023·北京顺义·统考一模）给出如下定义：对于线段PQ，以点P为中心，把点逆时针旋转60°得到点R，点R叫做线段PQ关于点P的“完美点”，例如等边△ABC中，点C就是线段AB关于点A的“完美点”．
在平面直角坐标系xOy中．
(1)已知点A0,2，在A13,1，A2−3,1，A31,3，A41,−3中，_____是线段OA关于点O的“完美点”；
(2)直线y=x+4上存在线段BB'，若点B'恰好是线段BO关于点B的“完美点”，求线段BB'的长；
(3)若OC=4，OE=2，点D是线段OC关于点O的“完美点”，点F是线段EO关于点E的“完美点”，当线段DF分别取得最大值和最小值时，直接写出线段CE的长．
题型07 利用等边三角形的性质与判定解决多结论问题
【例7】（2023·陕西宝鸡·校考一模）如图，在△ABC中，分别以AC，BC为边作等边△ACD和等边△BCE．设△ACD，△BCE，△ABC的面积分别是S1,S2,S3现有如下结论：①S1:S2=AC2:BC2；②连接AE，BD，则△BCD≌△ECA；③若AC⊥BC，则S1⋅S2=34S32，其中正确结论的序号是（ ）

A．①②B．①③C．①②③D．②③
【变式7-1】（2023·广东广州·统考一模）如图，菱形ABCD中，AB=AC，点E、F分别为边AB、BC上的点，且AE=BF，连接CE、AF交于点H，连接DH交AC于点O．则下列结论：①△ABF≌△CAE，②∠AHC=120°，③AH+CH=DH，④AD2=OD⋅DH中，正确的是 ．（填序号）

【变式7-2】（2023·广东珠海·珠海市紫荆中学校考三模）如图，Rt△ABC中，∠BAC=30°，以斜边AB和直角边AC为边分别作等边三角形△ABD和△ACE，F为AB的中点，连接DE交AB于点G，EF与AC交于点H．以下结论：① EF⊥AC；② 四边形ADFE为菱形；③ AD=4AG；④ AH·HC=EH·HF．其中正确的结论有 ．（填写所有正确结论的序号）

【变式7-3】（2023·贵州黔东南·统考一模）在Rt△ABC中，用尺规作图，分别以点A和点B为圆心，以大于12AB的长为半径作弧，两弧相交于点M和N，作直线MN交AB于点O，分别连接AM、BM、BN、AN、CO．则下列结论不一定正确的是（ ）
A．AM=ANB．CO=AOC．∠MAO=∠NAOD．∠CAN=∠NAO
考点三 线段垂直平分线的性质与判定定理
垂直平分线的概念：经过线段的中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线（或线段的中垂线）.
性质：线段的垂直平分线上的点到这条线段两个端点的距离相等.
判定：到一条线段两个端点距离相等的点在这条线段的垂直平分线上.
1. 对于含有垂直平分线的题目，首先考虑将垂直平分线上的点与线段两端点连接起来．
题型01 利用垂直平分线的性质求解
【例1】（2023·吉林长春·校考二模）如图，在△ABC中，∠ACB=90°，按下列步骤作图：①分别以点A和点C为圆心，大于AC一半的长为半径作圆弧，两弧相交于点M和点N；②作直线MN，与边AB相交于点D，与边AC相交于点E，连结CD．下列说法不一定正确的是（ ）

A．∠B=∠BDC B．∠ACD=∠A C．∠BCD+∠A=90°D．BC=2DE
【变式1-1】（2023·山东济宁·统考一模）如图，△ABC中，若∠BAC=80°，∠ACB=70°，根据图中尺规作图的痕迹推断，以下结论错误的是（ ）
A．∠BAQ=40°B．DE=12BD
C．AF=ACD．∠EQF=25°
【变式1-2】（2023·内蒙古包头·模拟预测）如图，在菱形ABCD中，分别以C、D为圆心，大于12CD为半径画弧，两弧分别交于点M、N，连接MN，若直线MN恰好过点A与边CD交于点E，连接BE，则下列结论错误的是（ ）

A．∠BCD=120°B．若AB=3，则BE=4
C．CE=12BCD．S△ADE=12S△ABE
【变式1-3】（2022·广东深圳·统考二模）如图，已知∠BAC=60°，AD是角平分线且AD=10，作AD的垂直平分线交AC于点F，作DE⊥AC，则△DEF周长为 ．
题型02 线段垂直平分线的判定
【例2】（2023·云南昭通·统考二模）如图，AC=BC，AD=BD，这个图形叫做“筝形”，数学兴趣小组几名同学探究出关于它的如下结论：①△ACD≌△BCD；②AO=BO；③AB⊥CD；④∠CAB=∠ABD．其中正确结论的序号是（ ）
A．①②③④B．①②③C．①②④D．②③④
【变式2-1】（2022·广东湛江·岭师附中校联考一模）如图，AB是⊙O的直径，CD是弦，CD⊥AB于点E，则下列结论中不成立的是（ ）

A．AC=ADB．CE=DEC．OE=BED．BD=BC
【变式2-2】（2022·湖北恩施·二模）如图，AD是△ABC的角平分线，DE、DF分别是△ABD和△ACD的高，求证：AD垂直平分EF．
题型03 线段垂直平分线的实际应用
【例3】（2023·湖南长沙·校考三模）《中共中央国务院关促进农民增加收入若干政策的意见》中提出“治理农村人居环境，搞好村庄治理规划和试点，节约农村建设用地”．政策出台后，湖南陆陆续续开展了村庄合并某地兴建的幸福小区的三个出口A、B、C的位置如图所示，物业公司计划在不妨碍小区规划的建设下，想在小区内修建一个电动车充电桩，以方便业主，要求到三个出口的距离都相等，则充电桩应该在三条边的 的交点处．

【变式3-1】（2022·陕西西安·校考模拟预测）如图，已知△ABC中，AB=AC，请利用尺规作图法，在BC上求作一点D，使得△ABD与△ACD的周长相等（保留作图痕迹，不写作法）．
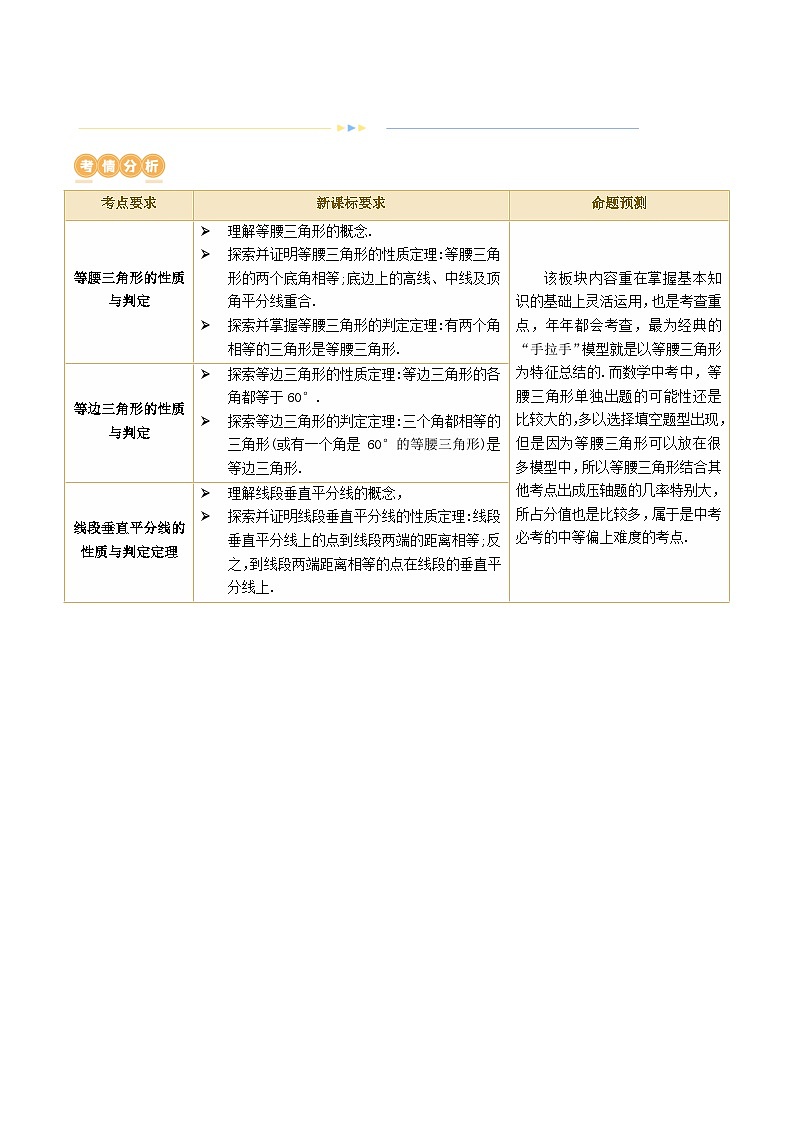
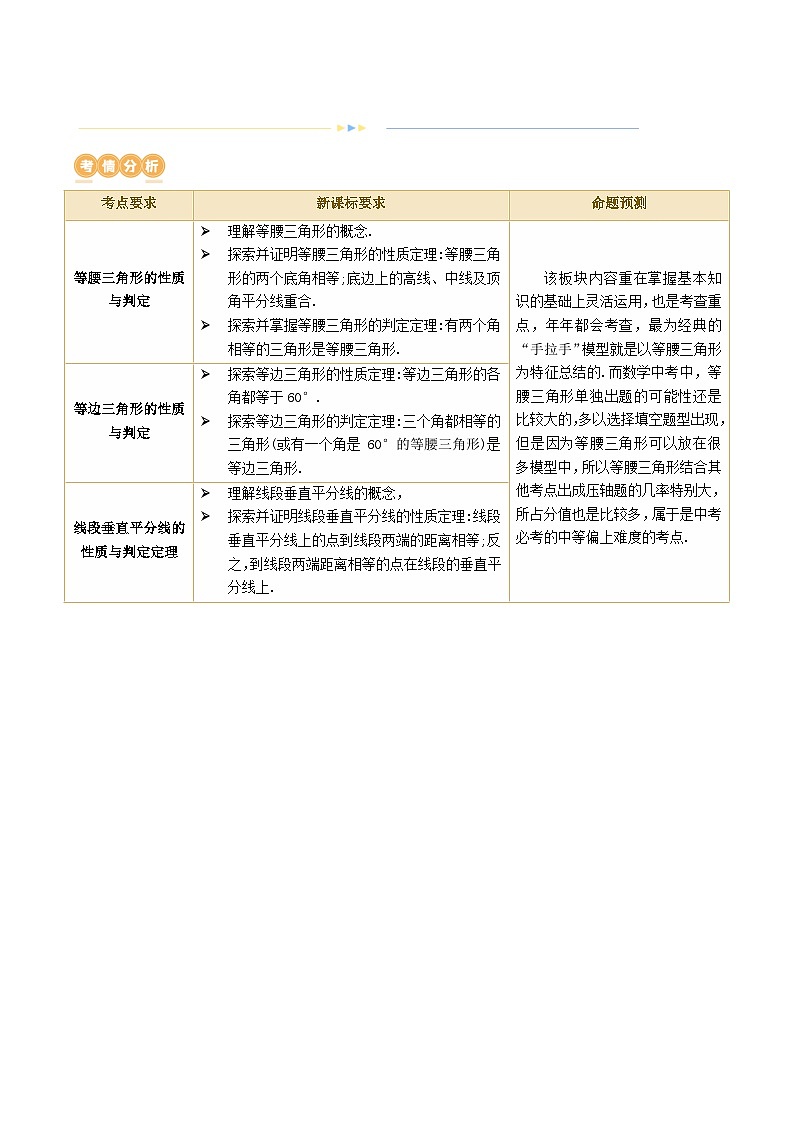
考点要求
新课标要求
命题预测
等腰三角形的性质与判定
理解等腰三角形的概念.
探索并证明等腰三角形的性质定理:等腰三角形的两个底角相等;底边上的高线、中线及顶角平分线重合.
探索并掌握等腰三角形的判定定理:有两个角相等的三角形是等腰三角形.
该板块内容重在掌握基本知识的基础上灵活运用，也是考查重点，年年都会考查，最为经典的“手拉手”模型就是以等腰三角形为特征总结的.而数学中考中，等腰三角形单独出题的可能性还是比较大的，多以选择填空题型出现，但是因为等腰三角形可以放在很多模型中，所以等腰三角形结合其他考点出成压轴题的几率特别大，所占分值也是比较多，属于是中考必考的中等偏上难度的考点.
等边三角形的性质与判定
探索等边三角形的性质定理:等边三角形的各角都等于60°.
探索等边三角形的判定定理:三个角都相等的三角形(或有一个角是 60°的等腰三角形)是等边三角形.
线段垂直平分线的性质与判定定理
理解线段垂直平分线的概念，
探索并证明线段垂直平分线的性质定理:线段垂直平分线上的点到线段两端的距离相等;反之，到线段两端距离相等的点在线段的垂直平分线上.