








人教版(2024)七年级上册(2024)6.1 几何图形多媒体教学ppt课件
展开1.为全面了解一个立体图形的形状,通常从______________ _______三个方向观察立体图形.
2.前面看和上面看________,前面看和左面看________ ,左面看和上面看________ .
3.有些立体图形是由一些平面图形围成的,将它们的表面适当展开,可以展开成平面图形.这样的平面图形称为相应立体图形的________。
我们可以用简单图形构造出复杂图形,也可以把复杂图形转化为简单图形进行研究。构成图形的元素是什么?这些元素之间又存在着什么关系?
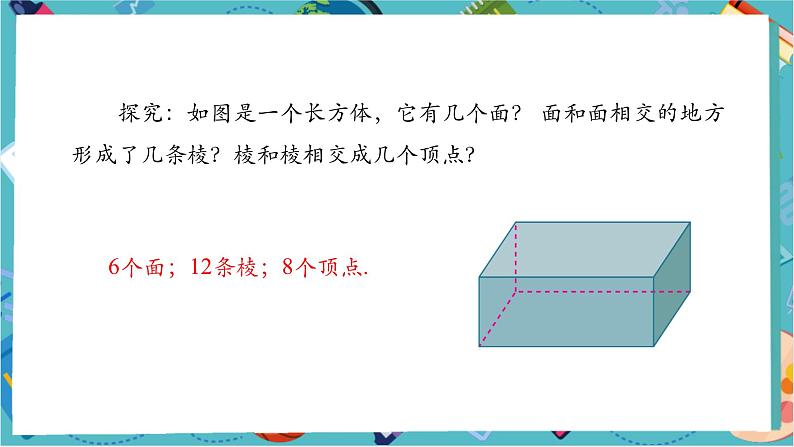
探究:如图是一个长方体,它有几个面? 面和面相交的地方形成了几条棱?棱和棱相交成几个顶点?
6个面;12条棱;8个顶点.
长方体、正方体、圆柱、圆锥、球、棱柱、棱锥等都是几何体.几何体也简称体。包围着体的是面。面有平的面和曲的面两种。
平静的水面给我们以平面的形象,而一些建筑物的屋顶(如图),则给我们以曲面的形象。
你能再举出一些平面与曲面的例子吗?
夜晚流星划过天空时留下一道明亮的光线,节日的焰火画出的曲线组成优美的图案,这些都给我们以线的形象。
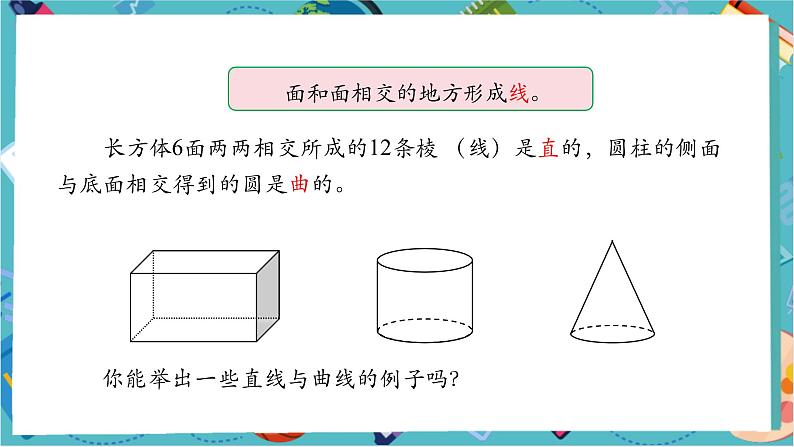
面和面相交的地方形成线。
长方体6面两两相交所成的12条棱 (线)是直的,圆柱的侧面与底面相交得到的圆是曲的。
你能举出一些直线与曲线的例子吗?
天上的星星、世界地图上的城市等都给我们以点的形象.
线和线相交的地方是点.
点只代表位置,没有大小,所以点都是相同的。
物体的运动会留下运动轨迹,这些运动轨迹往往也能抽象成几何图形。
笔尖可以看作一个点,这个点在纸上运动时,就形成线, 节日的焰火也可以看成由点运动形成的,这可以说点动成线。清洁玻璃时,刮窗器在玻璃上形成一个面 ,这可以说线动成面。长方形硬纸片绕它的一边旋转一周,形成一个圆柱体 ,这可以说面动成体。
几何图形都是由点、线、面、体组成的,点 是构成图形的基本元素.
点、线、面、体经过运动变化,就能组合成各种各样的几何图形,形成多姿多彩的图形世界.
一些庆祝 活动的背景也可以看作由点组成。
【知识技能类作业】必做题:
1.三棱柱有________个面,面与面相交的地方形成了_______条棱,棱与棱相交成________个顶点
2.四棱锥有________个面,面与面相交的地方形成了_______条棱,棱与棱相交成________个顶点
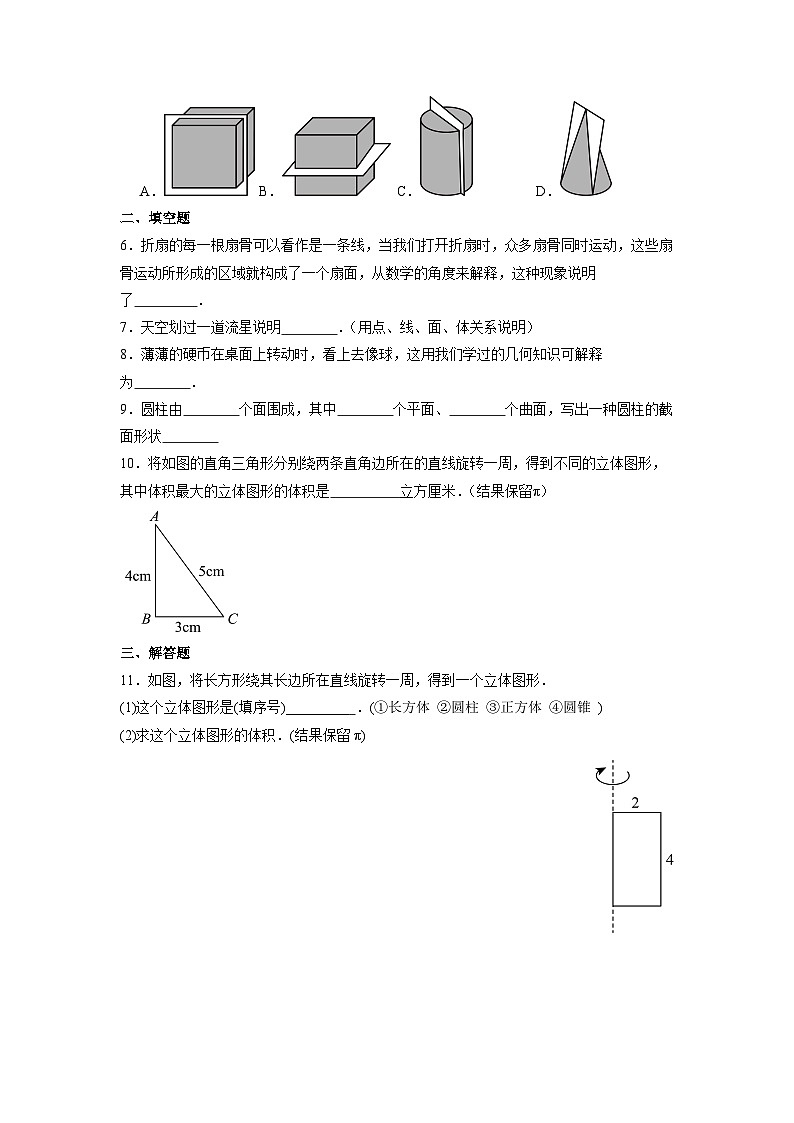
3.将下列选项中的图形绕轴旋转一周,可得到下面几何体的是( )
【知识技能类作业】选做题:
4.如图,上面的平面图形绕轴旋转一周,可以得出下面的立体图形,把有对应关系的平面图形与立体图形连接起来。
5.一个四棱柱每个侧面都是长2 cm,宽1 cm的长方形,则此四棱柱棱长之和为_________________.
16 cm或20 cm
1.圆锥是由________个面围成,其中________个平面,________个曲面; 2.球是由________个________面围成的.
3.下列现象能说明“面动成体”的是( ) A.时钟的钟摆摆动留下的痕迹 B.旋转一扇门,门在空中运动的轨迹 C.扔出一块小石子,石子在天空中飞行的路线 D.一根舞动的荧光棒
4.如图,正方形ABCD 的边长为2,将正方形绕直线l 旋转一周,所得圆柱从正面看得到的平面图形的周长为多少?
解:从正面看是一个长 为4,宽为2的长方形, 所以它的周长为: 2×(4+2)=12
初中数学人教版(2024)七年级上册(2024)6.1 几何图形作业课件ppt: 这是一份初中数学人教版(2024)七年级上册(2024)<a href="/sx/tb_c4050888_t3/?tag_id=26" target="_blank">6.1 几何图形作业课件ppt</a>,共10页。
数学七年级上册(2024)6.1 几何图形习题课件ppt: 这是一份数学七年级上册(2024)<a href="/sx/tb_c4050888_t3/?tag_id=26" target="_blank">6.1 几何图形习题课件ppt</a>,文件包含人教版七年级上册数学612《点线面体》pptx、人教版七年级上册数学612《点线面体》教案docx、人教版七年级上册数学612《点线面体》分层练习docx、人教版七年级上册数学612《点线面体》预习案docx等4份课件配套教学资源,其中PPT共30页, 欢迎下载使用。
初中数学人教版(2024)七年级上册(2024)6.1 几何图形教课ppt课件: 这是一份初中数学人教版(2024)七年级上册(2024)<a href="/sx/tb_c4050888_t3/?tag_id=26" target="_blank">6.1 几何图形教课ppt课件</a>,共15页。PPT课件主要包含了学习目标,新课引入,几何体,探究点1,获取新知,探究点2,包围着体的是面,探究点3,探究点4,例题讲解等内容,欢迎下载使用。













