2025年云南省昆明市第十四中学中考一模数学试题

这是一份2025年云南省昆明市第十四中学中考一模数学试题，文件包含20242025学年上学期九年级一模模拟考试数学docx、数学答案pdf等2份试卷配套教学资源，其中试卷共16页， 欢迎下载使用。


注意事项：
1.满分100分，答题时间为120分钟。
2.请将各题答案填写在答题卡上。
一、选择题(本大题共12小题，每小题3分，共36分，在每个小题给出的四个选项中，只有一项符合题目要求)
1.下面四个图形分别是绿色食品、节水、节能和回收的标志，在这四个标志中，是中心对称图形的是
2.若关于x的方程( m+1x²+mx−1=0是一元二次方程，则m的取值范围是
A. m≠-1 B. m=1 C. m>1 D. m≠0
3.抛物线 y=x²−4x+3的顶点坐标是
A.(2,1) B.(2,-1) C.(-2,1) D.(-2,-1)
4.若x=a是方程. x²+2x−2=0的一个根，则代数式 2a²+4a+2019的值为
A.2021 B.2022 C.2023 D.-2023
5.用配方法解方程 x²+4x+1=0,变形后的结果正确的是
A.x+2²=5 B.x+4²=3
C.x+2²=3 D.x+4²=5
6.关于二次函数 y=−2x+2²−3的图象与性质，下列说法正确的是
A.对称轴是直线x=2，最小值是-3
B.对称轴是直线x=2，最大值是-3
C.对称轴是直线x=-2，最小值是-3
D.对称轴是直线x=-2，最大值是-3
7.如图,将Rt△ABC绕直角顶点C 顺时针旋转90°,得到△DEC,连接AD,若 ∠BAC=20°,则∠BAD=
A.45°
B.50°
C.60°
D.65°

【数学 第1页(共8页)】
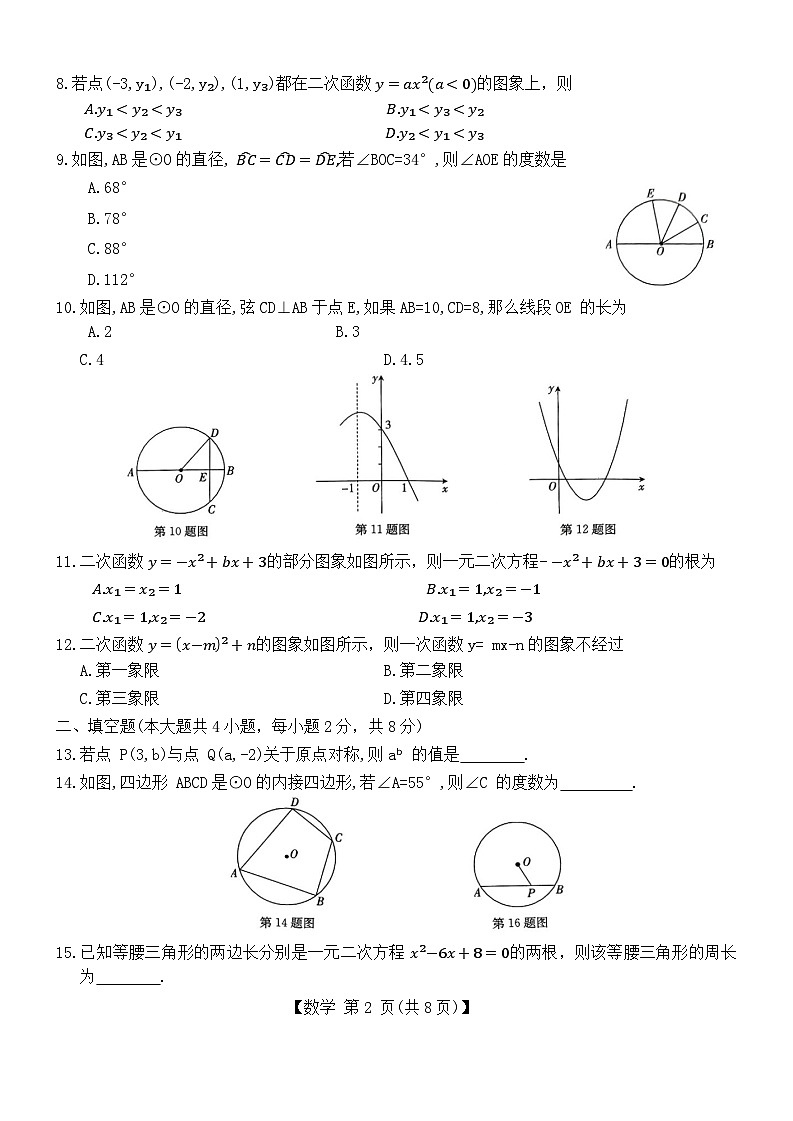
8.若点(-3,y₁),(-2,y₂),(1,y₃)都在二次函数 y=ax²(a<0)的图象上，则
A.y₁ C.y₃9.如图,AB是⊙O的直径, BC=CD=DE,若∠BOC=34°,则∠AOE的度数是
A.68°
B.78°
C.88°
D.112°
10.如图,AB是⊙O的直径,弦CD⊥AB于点E,如果AB=10,CD=8,那么线段OE 的长为
A.2 B.3
C.4 D.4.5
11.二次函数 y=−x²+bx+3的部分图象如图所示，则一元二次方程- −x²+bx+3=0的根为
A.x₁=x₂=1 B.x₁=1,x₂=−1
C.x₁=1,x₂=−2 D.x₁=1,x₂=−3
12.二次函数 y=x−m²+n的图象如图所示，则一次函数y= mx-n的图象不经过
A.第一象限 B.第二象限
C.第三象限 D.第四象限
二、填空题(本大题共4小题，每小题2分，共8分)
13.若点 P(3,b)与点 Q(a,-2)关于原点对称,则aᵇ的值是 .
14.如图,四边形 ABCD是⊙O的内接四边形,若∠A=55°,则∠C 的度数为 .
15.已知等腰三角形的两边长分别是一元二次方程 x²−6x+8=0的两根，则该等腰三角形的周长为 .
【数学 第2 页(共8页)】 16.如图,⊙O的直径为20,弦 AB=16,P是弦AB 上一动点，则OP长的取值范围是 .
三、解答题(本大题共8小题，共56分，解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分6分)
解一元二次方程： x³−2x=15=0.
18.(本小题满分6分)
往一个圆柱形管道内注入一些水以后，发现其横截面如图所示，若水面宽AB 为24 cm，水的最大深度CD为8cm，求圆柱形管道横截面的直径.
【数学 第3页(共8页)】19.(本小题满分7分)
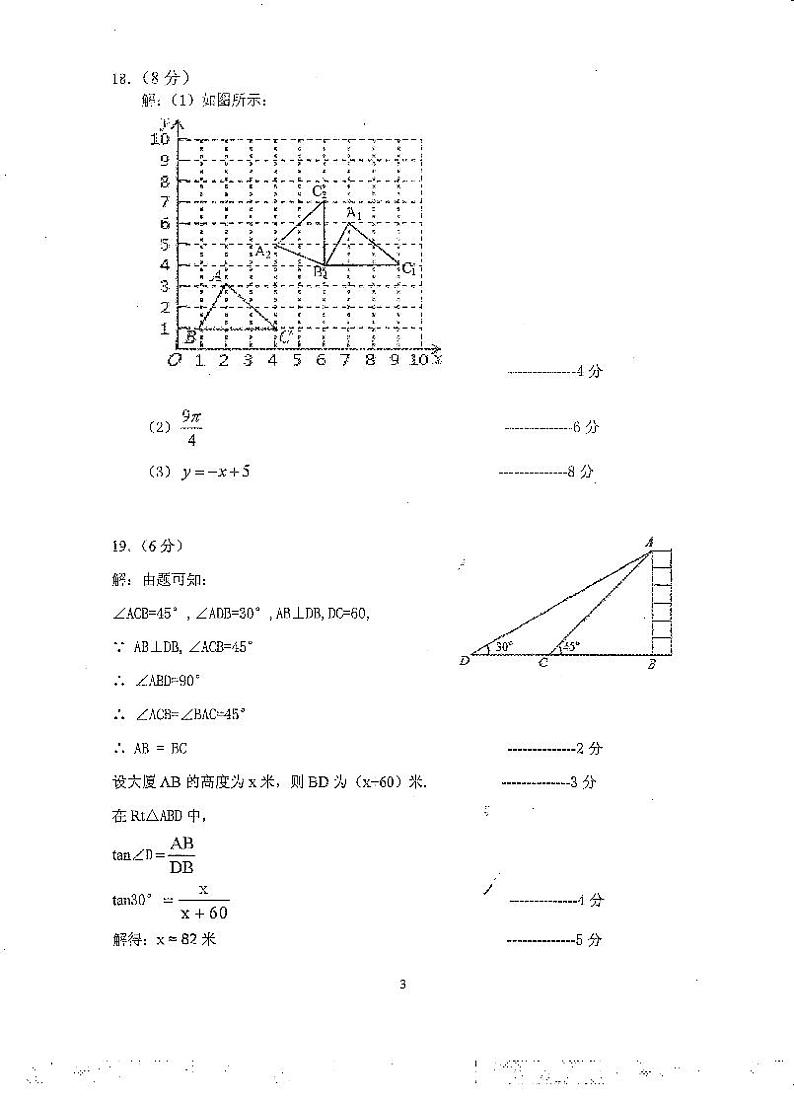
如图， △ABC的三个顶点的坐标分别为A(-6.4). B(-4.0),C(-2.2).
(1)将 △ABC向右平移5个单位长度，得到 △A₁B₁C₁,请画出该图形.
(2)将 △ABC绕坐标原点O逆时针旋转 90°,得到 △A₂B₂C₂,画出该图形，并直接写出点 A₂的坐标.
20.(本小题满分7分)
已知抛物线 y=x²−2mx+m²−9.
(1)求证：抛物线与x轴有两个不同的交点.
(2)当 m=1时，抛物线与x轴交于点A，B，求AB的长.
【数学 第4页(共8页)】 21.(本小题满分7分)
如图,AB为⊙O的直径,AC为⊙O的弦. ∠ACB的平分线交⊙O于点 D.
(1)若∠ADC=35°,求∠CAB的度数.
(2)若AB=6,求△ABD的面积.
【数学 第5页(共8页)】 22.(本小题满分7分)
某超市以每千克30元的价格购进一种干果，计划以每千克60元的价格销售，为了让顾客得到实惠，现决定降价销售，已知这种干果销售量y(千克)与每千克降价 x(0(1)求y与x之间的函数关系式.
(2)当这种干果每千克降价多少元时，超市获利最大，最大利润是多少元?
【数学 第6页(共8页)】 23.(本小题满分8分)
如图，在等腰直角 △ABC中， ∠ABC=90°,点D在AC上，将 △ABD绕顶点 B 沿顺时针方向旋转 90°得到 △CBE.
(1)求 ∠DCE的度数.
(2)若 AD=5,CD=35,求 BD 的长.
【数学 第7页(共8页)】 24.(本小题满分8分)
如图，抛物线与x轴交于 A−10,,B两点,与y轴交于点C,且满足OB=OC=3OA.
(1)求抛物线的解析式.
(2)M是线段BC上的一点(不与点B，C重合)，过点M作NM∥y轴交抛物线于点 N，交x轴于点D，连接NB，NC，若点M的横坐标为m，是否存在点 M，使 △BNC的面积最大?若存在，求m的值；若不存在，请说明理由.
【数学 第8页(共8页)】