2024-2025学年上海市浦东区高二上学期期中联考数学检测试题（含解析）

这是一份2024-2025学年上海市浦东区高二上学期期中联考数学检测试题（含解析），共16页。试卷主要包含了填空题，单选题，解答题等内容，欢迎下载使用。
1．用符号表示“平面与相交于直线” ．
2．在正方体中，与直线异面的直线是 ．（写出一个即可）.
3．空间中，斜线与平面所成角的取值范围为 ．（用弧度制表示）．
4．命题：“若两个平面垂直，那么过第一个平面上一点且垂直于第二个平面的直线，不一定在第一个平面上.”上述命题为 （选填“真命题”或“假命题”）．
5．现行国际比赛标准排球的直径约为，在忽略材料厚度和制造误差的情况下，则排球的表面积大约为 ．
6．如图，矩形是由斜二侧画法得到的水平放置的一个平面图形的直观图，其中，，则原图形面积为 ．
7．某圆锥的母线长为，侧面积展开图的圆心角为的扇形，则该圆锥的底面半径为 ．
8．如图是一个正方体的平面展开图，将这个正方体复原后，在其所有棱以及三条面对角线、、中，直线与直线所成角为 ．
9．一个圆柱的外接球的体积为，该圆柱的轴截面是一个正方形，则该圆柱的底面面积为 ．
10．三棱锥的侧棱两两垂直，三个侧面三角形的面积分别为，则三棱锥的体积是 ．
11．空间中存在三条不同的直线，直线与直线所成角为，直线与直线所成角为，直线与直线所成角的取值范围为 ．（用弧度制表示）.
12．我国历史文化悠久，“爰”铜方彝是商代后期的一件文物，其盖似四阿式屋顶，盖为子口，器为母口，器口成长方形，平沿，器身自口部向下略内收，平底、长方形足、器内底中部及盖内均铸一“爰”字.通高24cm，口长13.5cm，口宽12cm，底长12.5cm，底宽10.5cm．现估算其体积，上部分可以看作四棱锥，高约8cm，下部分看作台体.则其体积约为 （精确到0.1）．（参考数据：，）
二、单选题（本大题共4小题）
13．设、是平面外的两条直线，且，那么是的（ ）条件
A．充分非必要B．必要非充分
C．充要D．既非充分又非必要
14．下列命题正确的是（ ）
A．过直线外一点有且只有一条直线与该直线垂直
B．过平面外一点有且只有一条直线与该平面平行
C．过平面外一点有且只有一个平面与该平面垂直
D．过平面外一点有且只有一个平面与该平面平行
15．若直线垂直于以为直径的圆所在的平面，为圆周上异于的一点，下列说法错误的是（ ）
A．B．
C．D．平面
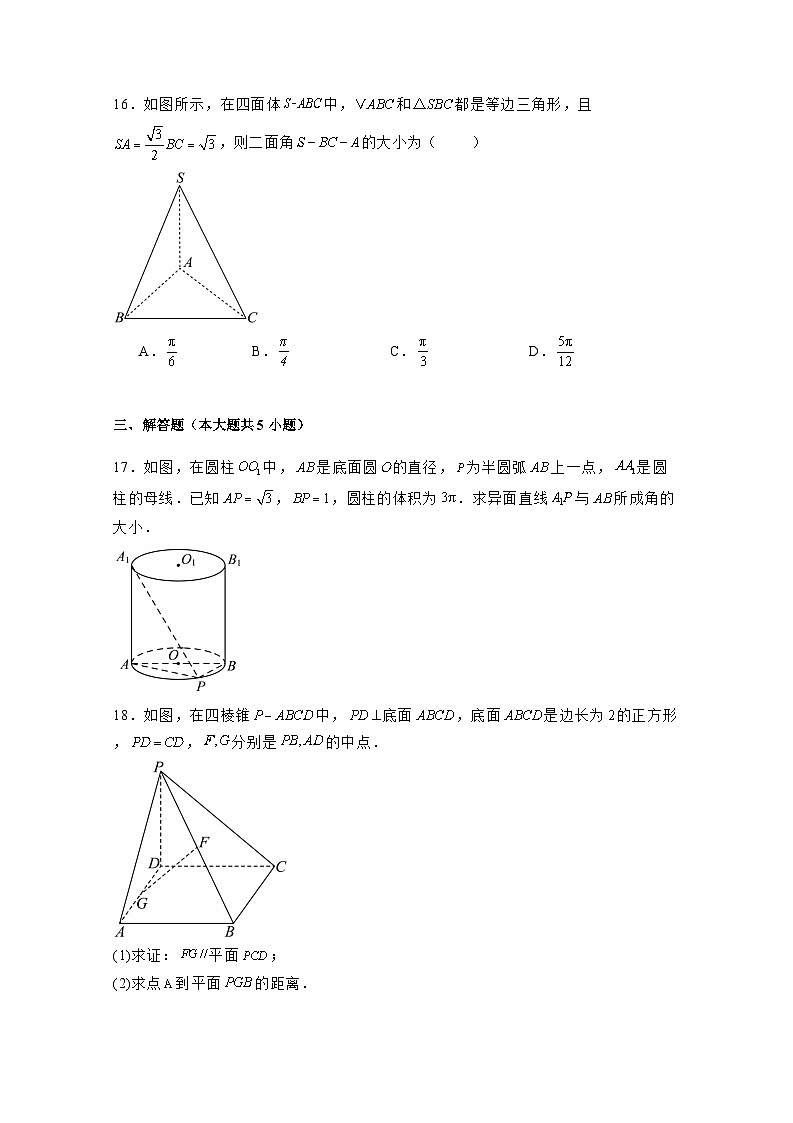
16．如图所示，在四面体中，和都是等边三角形，且，则二面角的大小为（ ）
A．B．C．D．
三、解答题（本大题共5小题）
17．如图，在圆柱中，是底面圆的直径，为半圆弧上一点，是圆柱的母线．已知，，圆柱的体积为．求异面直线与所成角的大小．
18．如图，在四棱锥中，底面，底面是边长为的正方形，，分别是的中点．
(1)求证：平面；
(2)求点到平面的距离．
19．如图，直三棱柱中，，，是的中点，是的中点．
(1)求证：直线与直线垂直；
(2)求直线与平面所成的角的大小．
20．如图，在四棱锥中，平面平面，，四边形为正方形，为的中点，为上一点，为上一点，且平面平面．

(1)求证：为线段中点；
(2)求二面角的正切值；
(3)在棱上是否存在点，使得平面平面？若存在，求；若不存在，说明理由．
21．设计一个帐篷，它下部的形状是正四棱柱，上部的形状是正四棱锥，且该帐篷外接于球（如图所示）．

(1)若正四棱柱是棱长为的正方体，求该帐篷的顶点到底面中心的距离；
(2)若该帐篷外接球的半径，设，该帐篷的体积为，则当为何值时，体积取得最大值．
答案
1．【正确答案】
【详解】“平面与相交于直线”的符号表示，
故答案为.
2．【正确答案】（或或或，答案不唯一）
【详解】如图，由异面直线的定义知，直线异面的直线是等，
故（或或或，答案不唯一）.
3．【正确答案】
【详解】根据斜线与平面所成角的定义可知，空间中，斜线与平面所成角的范围是.
故答案为.
4．【正确答案】假命题
【详解】如图，我们将垂直的两个平面记为，两条直线分别记为，点记为，

由题意得，，且设，
过点作，故，
由面面垂直的性质得，因为过一点有且只有一条直线与垂直，
所以直线与直线重合，故.
故假命题.
5．【正确答案】
【详解】由题意知，排球半径，
则表面积.
故答案为.
6．【正确答案】
【详解】依题意，矩形的面积，
由原图形面积是直观图面积的，得原图形面积.
故
7．【正确答案】
【详解】设圆锥的底面半径为，由题有，解得.
故答案为.
8．【正确答案】/60°
【详解】将正方体的平面展开图还原成正方体，如图所示，连接，
易知，则或其补角为直线与直线所成的角，
在中，易知，所以，
故答案为.
9．【正确答案】
【详解】设圆柱的底面半径为，则母线长为，外接球的半径为，
由题有，则，解得，
所以圆柱的底面面积为，
故答案为.
10．【正确答案】
【详解】如图，两两垂直，又面，则面，
则三棱锥的体积,
又三个侧面三角形的面积分别为，不妨设，
则，得到,
所以，
故答案为.
11．【正确答案】
【详解】过三条直线外任一点分别作的平行线，
则直线与直线所成角即所成角为，
直线与直线所成角即所成角为，
直线与直线所成角即即所成角.
如图，根据题意构造两个圆锥，由题意知，

其中底面圆心为，轴所在直线为，
小圆锥的母线所在直线为，轴截面；
大圆锥的母线所在直线为，轴截面，且在一条直线上.
由题意，，
由图可知，当移动到，移动到时，可得与所成角的最小，
最小值为.
当移动到，移动到时，可得与所所成角的最大，
最大值为，
当与所在直线重合，直线绕点在小圆锥表面从连续运动至，
直线与所成角连续变化且越来越大，从增至.
所以与所成角的取值范围为.
故答案为.
12．【正确答案】
【详解】由题意可得：
，
，
所以几何体的体积.
故答案为.
13．【正确答案】A
【详解】证明充分性：若，结合，且b在平面M外，可得，是充分条件；
证明必要性：若，结合，且a，b是平面M外，则a，b可以平行，也可以相交或者异面，所以不是必要条件．
故是的“充分非必要”
故选：A．
14．【正确答案】D
【详解】对于A选项，过直线外一点有无数条直线与这条直线垂直，
且这无数条直线均相交于这个点（即与它垂直的平面内的任意一条过该点的直线），A错；
对于B选项，过平面外一点，有无数条直线与这个平面平行，
且这无数条直线均相交于这个点（即与它平行的平面内的任意一条过该点的直线），B错；
对于C选项，过平面外一点，有且只有一条直线与这个平面垂直，
若将过该直线的平面绕这条直线旋转，则可以得到无数个平面与已知平面垂直，C错；
对于D选项，由B选项可知，过平面外一点，有无数条直线与这个平面平行，
且这无数条直线均相交于这个点，并且这无数条直线共面，
故过平面外一点有且只有一个平面与该平面平行，D对.
故选：D.
15．【正确答案】A
【详解】因为直线垂直于以为直径的圆所在的平面，
又面，所以，故选项C正确，
又，，面，所以平面，
又面，所以，故选项B和D正确，
对于选项A，若，又，面，
则面，又面，所以，与相矛盾
故选：A.
16．【正确答案】C
【详解】取中点，连接，因为和都是等边三角形，
则，所以为二面角的平面角，
又，则，，所以，
所以二面角的大小为.
故选：C.
17．【正确答案】
【详解】由题意知，则异面直线与所成角即为，
又，
在中，又，
，
．
则异面直线与所成角的大小为．
18．【正确答案】(1)证明见解析
(2)
【详解】（1）取的中点为，连接，
在中，为的中位线，
.
又在正方形中，且，
，且
又是的中点，
，且，
四边形为平行四边形，.
又平面，平面
平面.
（2）连接.
由题意，在四棱锥中，平面，
为三棱锥的高.
又平面，则.
设点到平面的距离为，
则有，则，（）
由题意，，则，
由为的中点，则，
所以，
，
所以，且，
代入（）化简可得，解得，
点A到平面的距离为.
19．【正确答案】(1)证明见解析
(2)（或或）
【详解】（1）取的中点，联结，，
因为，分别是、的中点，所以，，
又因为直棱柱中，可得，
又，面，所以平面，
又平面，所以.
（2）平面，平面
可得，又，即，又，面，
平面
为直线与平面所成角，且，所以，
假设，则，所以，，
得到，所以，
所以直线与平面所成角为（或或）.
20．【正确答案】(1)证明见解析
(2)
(3)存在，且
【详解】（1）证明：因为平面平面．平面平面，平面平面，
可得，
又因为，则四边形为平行四边形，则，
因为为的中点，则，所以，，
故点为的中点.
（2）解：因为，为的中点，则，
因为平面平面，平面平面，平面，
所以，平面，
又因为四边形为正方形，以点为坐标原点，、、的方向分别为、
、轴的正方向建立如下图所示的空间直角坐标系，

因为，则、、，
设平面的法向量为m=x1,y1,z1，，，
则，取，可得，
易知平面的一个法向量为，，
则，
所以，.
由图可知，二面角的平面角为锐角，
因此，二面角的正切值为.
（3）解：易知、、、，
设，其中，
则，，
设平面的法向量为，
则，
取，则，
因为平面平面，则，
则，解得，
所以，当点为的中点时，平面平面，故.
21．【正确答案】(1)
(2)
【分析】（1）根据条件，利用外接球的球心为正方体的中心，可得，即可求出结果；
（2）根据条件得到，令，得到，再利用导数与函数单调性间的关系，求出的单调区间，即可求解.
【详解】（1）设外接球的半径为，因为正四棱柱是棱长为的正方体，
易知外接球的球心为正方体的中心，所以，而，
得到．
（2），
，
．
，
令，
由，得到，
在上递增，在递减．
时，体积取得最大值．