2023-2024学年江西省宜春市高三（上）期末数学试卷

这是一份2023-2024学年江西省宜春市高三（上）期末数学试卷，共5页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。
1．已知复数满足，则复数的虚部为（ ）
A．B．C．D．
2．已知，则的最小值为（ ）
A．6B．8C．9D．10
3．加强学生心理健康工作已经上升为国家战略，为响应国家号召，W区心理协会派遣具有社会心理工作资格的3位专家去定点帮助5名心理特异学生.若要求每名学生只需一位专家负责，每位专家至多帮助两名学生，则不同的安排方法共有（ ）种
A．90B．125C．180D．243
4．表示不超过的最大整数，如，，已知数列满足，，，若，为数列的前项和，则（ ）
A．B．C．D．
5．抛物线C：的焦点为F，其准线与x轴的交点为K，P为准线上一点，线段PF与抛物线交于M点，若是斜边长为的等腰直角三角形，则（ ）
A．B．
C．D．
6．在平面直角坐标系中，点，，，是圆上一点，是边上一点，则的最大值是（ ）
A．B．
C．D．
7．已知，，，则（ ）
A．B．C．D．
8．已知双曲线的左、右顶点分别为为的右焦点，的离心率为2，若为右支上一点，，记，则（ ）
A．B．1C．D．2
二、多选题（20分）
9．下列关于概率统计说法中正确的是（ ）
A．两个变量的相关系数为，则越小，与之间的相关性越弱
B．设随机变量，若，则
C．在回归分析中，为0.89的模型比为0.98的模型拟合得更好
D．某人解答10个问题，答对题数为，则
10．已知定义在R上的函数满足，且是奇函数，则（ ）
A．的图象关于点对称B．
C．D．若，则
11．已知抛物线的焦点为，过点的直线与抛物线交于两点（在第一象限），为坐标原点，若，则（ ）
A．B．直线的斜率是
C．线段的中点到轴的距离是D．的面积是
12．在三棱锥中，平面为内的一个动点（包括边界），与平面所成的角为，则（ ）
A．的最小值为B．的最大值为
C．有且仅有一个点，使得D．所有满足条件的线段形成的曲面面积为
三、填空题（20分）
13．的展开式中的系数是 （用数字作答）．
14．函数的图象在处的切线与坐标轴所围成的图形的面积为 .
15．若关于x的方程在区间上至少有两个不同的实根，则实数a的取值范围是 ．
16．已知椭圆的左､右焦点分别为，离心率为，点在椭圆上，连接并延长交于点，连接，若存在点使成立，则的取值范围为 .
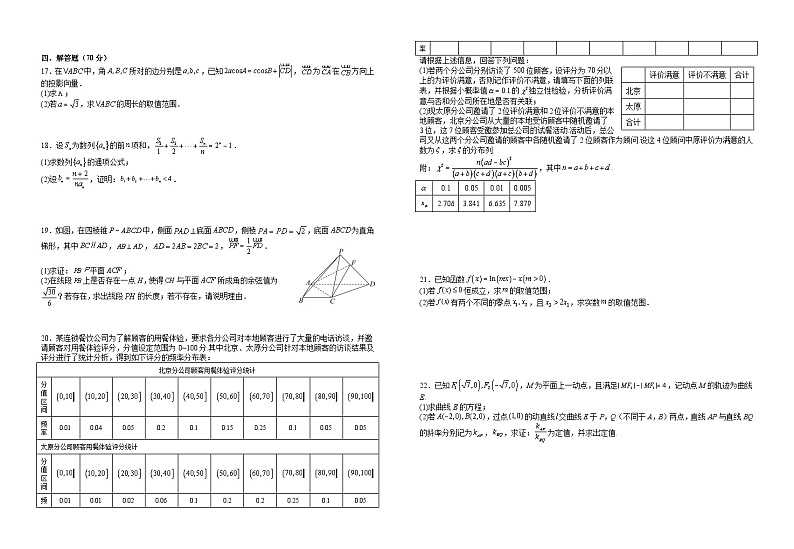
四、解答题（70分）
17．在中，角所对的边分别是，已知，为在方向上的投影向量．
(1)求；
(2)若，求的周长的取值范围．
18．设为数列的前项和，．
(1)求数列的通项公式；
(2)设，证明：．
19．如图，在四棱锥中，侧面底面，侧棱，底面为直角梯形，其中，，，．

(1)求证：平面；
(2)在线段上是否存在一点H，使得与平面所成角的余弦值为？若存在，求出线段的长度；若不存在，请说明理由．
20．某连锁餐饮公司为了解顾客的用餐体验，要求各分公司对本地顾客进行了大量的电话访谈，并邀请顾客对用餐体验评分，分值设定范围为0~100分.其中北京、太原分公司针对本地顾客的访谈结果及评分进行了统计分析，得到如下评分的频率分布表：
请根据上述信息，回答下列问题：
(1)若两个分公司分别访谈了500位顾客，设评分为70分以上的为评价满意，否则记作评价不满意，请填写下面的列联表，并根据小概率值的独立性检验，分析评价满意与否和分公司所在地是否有关联；
(2)现太原分公司邀请了2位评价满意和2位评价不满意的本地顾客，北京分公司从大量的本地受访顾客中随机邀请了3位，这7位顾客受邀参加总公司的试餐活动.活动后，总公司又从这两个分公司邀请的顾客中各随机邀请了2位顾客作为顾问.设这4位顾问中原评价为满意的人数为，求的分布列.
附：，其中.
21．已知函数．
(1)若恒成立，求的取值范围；
(2)若有两个不同的零点，且，求实数的取值范围．
22．已知，M为平面上一动点，且满足，记动点M的轨迹为曲线E.
(1)求曲线E的方程；
(2)若，过点的动直线交曲线E于P，Q（不同于A，B）两点，直线AP与直线BQ的斜率分别记为，，求证：为定值，并求出定值.
江西省宜春市宜丰县宜丰中学2023-2024学年高三上学期期末数学参考答案
1．A 2．C 3．A 4．B 5．D
6．B【详解】解：设，则，所以，
因为，所以当，即点与点重合时，有最大值，所以问题转化为在圆上，求的最大值，
因为点在圆上，设点所在的直线为，因为直线与圆有公共点，
所以圆心到直线的距离不大于半径，即，所以，解得，即，
所以，所以的最大值是12，故选：B
7．A【详解】设，，则，则在单调递增，故，即，则，且.，且所以，
则；因为，则，则，
所以，由，则，即.
所以.故选：A
8．A【详解】设的焦距为，点，由的离心率为2可知，因为，所以，将代入的方程得，即，所以，故．故选:A．
9．BD 10．ABD
11．ACD【详解】由题意可得直线的斜率不为0，则可设直线，联立整理得，则，因为，所以，所以，所以，所以，则，即，解得，因为，所以，解得，则A正确；对于B，因为，所以，则直线的斜率是，因为点在第一象限，所以直线的斜率大于0，所以直线的斜率是，则B错误；对于C，设线段的中点为，则，即线段的中点到轴的距离是，则C正确；对于D，因为，所以，则的面积，故D正确.故选：ACD.
12．ACD【详解】因为平面，平面，所以，
又，所以，取的中点，则，所以平面，过作于，因为平面，所以，又平面，所以平面，所以为与平面所成的角的平面角（或补角），因为平面，平面，则，又在中，，则，所以，
因为，所以，，所以点轨迹是以为圆心，以为半径的圆在内部的一部分，如图，所以的最小值为，故正确；由于轨迹圆部分在平面外部，所以的最大值不等于，故B错误；因为平面，平面，所以，若，则点在线段上，有且仅有一个点满足题意，故C正确；动线段形成的曲面为圆锥侧面积的一部分，易知三棱锥是正三棱锥，平面，故为等边的中心，所以，
因为，所以，因为，所以曲面面积为圆锥侧面面积的，圆锥侧面积为，所以所有满足条件的动线段形成的曲面面积为，故D正确.故选：ACD.
13． 14．1
15．【详解】因为，
.
所以由得，
即.当时，无解，即.下面讨论方程，在上至少有一个实根的情况：因为原方程在区间上至少有两个不同的实根，所以，得且方程，在上至少有一个实根.
令，则.当时，，方程不成立；当时.
令，易知在上单调递减，得，
在上也单调递减，得，所以，使得方程在上至少有一个实根要满足，在上至少有一个实根要满足.综上所述，方程在区间上至少有两个不同的实根，则实数a的取值范围是.故答案为：.
16．【详解】设，则.显然当靠近右顶点时，，所以存在点使等价于，在中由余弦定理得，即，解得 ，同理可得，所以，所以，所以，当且仅当时等号成立.由得，所以.
17．(1) (2)
【详解】（1）由为在方向上的投影向量知，，所以，
由正弦定理得，又，所以，又．所以；
（2）由正弦定理得．所以
，因为，所以，所以，所以，所以，故的周长的取值范围是．
18．【详解】（1）当时，，当时，，
两式相减得，则，当时，，
又当时，，当时，，则，显然符合，
所以数列的通项公式是.
（2）由（1）知，，所以.
19．【详解】（1）连接交于M，，，，，
，，又平面，平面，平面．
（2）设线段上存在一点H，使得与平面所成角的余弦值为，即与平面所成角的正弦值为，设，取中点O，连接，，侧面底面，侧面底面，侧面，
底面，∵，，
以O为坐标原点，分别以所在直线为轴建立如图所示的空间直角坐标系，则，
则，设平面的一个法向量为，
则令，则，∴平面的一个法向量为，又，，又，，设与平面所成角，则，整理得，解得或，当时，，当时，
故在线段上存在一点H，使得与平面所成角的余弦值为，或
20．【详解】（1）由题意及表格得，北京分公司顾客用餐体验评价满意的有人，则不满足的有人，太原分公司顾客用餐体验评价满意的有人，则不满足的有人，填写列联表如下：零假设为：评价满意与否和分公司所在地相互独立，即两个分公司的评价满意没有差异.根据列联表中的数据，经计算得到：，根据小概率值的独立性检验，有充分证据推断不成立，所以认为评价满意与否和分公司所在地有关联.
（2）由题意及（1）得，所有可能的取值为0，1，2，3，4.；；；
；所以的分布列如下：
21．【详解】（1）的定义域为，令，得，令，则，
令，可得，当时，；当时，．所以在区间上单调递减，在区间上单调递增．所以，所以．
（2），两式相减，得．令，则，故，记，则，构造函数，，所以在上递减，由于，所以当时，，所以，
所以函数在区间上单调递减，故，即，而，在区间上单调递减，故，即．
22．【详解】（1）由题可知，则的轨迹是实轴长为，焦点为即的双曲线的右支，则，所以曲线的方程为：(或).
（2）由题可知过点的动直线斜率存在且不为，则设斜率为，
所以直线的方程为：，设，，
联立 ，可得，
则 ，可得，即或，
则
，所以为定值，定值为.北京分公司顾客用餐体验评分统计
分值区间
频率
0.01
0.04
0.05
0.2
0.1
0.15
0.25
0.1
0.05
0.05
太原分公司顾客用餐体验评分统计
分值区间
频率
0.01
0.01
0.02
0.06
0.1
0.2
0.2
0.25
0.1
0.05
评价满意
评价不满意
合计
北京
太原
合计
0.1
0.05
0.01
0.005
2.706
3.841
6.635
7.879
评价满意
评价不满意
合计
北京
100
400
500
太原
200
300
500
合计
300
700
1000
0
1
2
3
4
P