2023-2024学年河北省石家庄重点中学八年级（上）期末数学试卷（含解析）

这是一份2023-2024学年河北省石家庄重点中学八年级（上）期末数学试卷（含解析），共19页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1.下列各数中，无理数的是( )
A. 6B. 25C. 713D. 3.1415
2.若 x+2x有意义，则实数x的取值范围为( )
A. x>−2B. x≥−2C. x>−2且x≠0D. x≥−2且x≠0
3.等腰三角形的两边长分别是2，4，则第三边长为( )
A. 2B. 4C. 2或4D. 3或4
4.下列式子为最简二次根式的是( )
A. 14B. 12C. 4D. 1 2
5.如图，BE=CF，AE⊥BC，DF⊥BC，要根据“HL”证明Rt△ABE≌Rt△DCF，则还要添加一个条件是( )
A. AB=DC
B. ∠A=∠D
C. ∠B=∠C
D. AE=BF
6.围棋起源于中国，古代称之为“弈”，至今已有4000多年的历史.以下是在棋谱中截取的四个部分，由黑白棋子摆成的图案是中心对称图形的是( )
A. B. C. D.
7.估计 5+2的值在( )
A. 2和3之间B. 3和4之间C. 4和5之间D. 5和6之间
8.化简分式7a+7b(a+b)2的结果是( )
A. a+b7B. 7a+bC. a−b7D. 7a−b
9.矩形相邻两边长分别为 2， 8，则它的周长和面积分别是( )
A. 10，4B. 2 10，4C. 4，3 2D. 6 2，4
10.AD是Rt△ABC的角平分线，若AB=4，BD=3，则点D到AC距离为( )
A. 3
B. 4
C. 5
D. 6
11.如图，在Rt△ABC中，∠B=90°，∠A=40°，AC的垂直平分线MN与AB交于点D，则∠BCD的度数是( )
A. 10°
B. 15°
C. 20°
D. 25°
12.如图，若△ABC≌△ADE，则下列结论中不成立的是( )
A. ∠BAD=∠CAE
B. ∠BAD=∠CDE
C. DA平分∠BDE
D. AC=DE
13.下列命题正确的是( )
A. 两边及一角对应相等的两个三角形全等
B. 将32000精确到千位，记为3.20×104
C. 16的平方根是4
D. 到三角形三个顶点距离相等的点在这个三角形三边的垂直平分线上
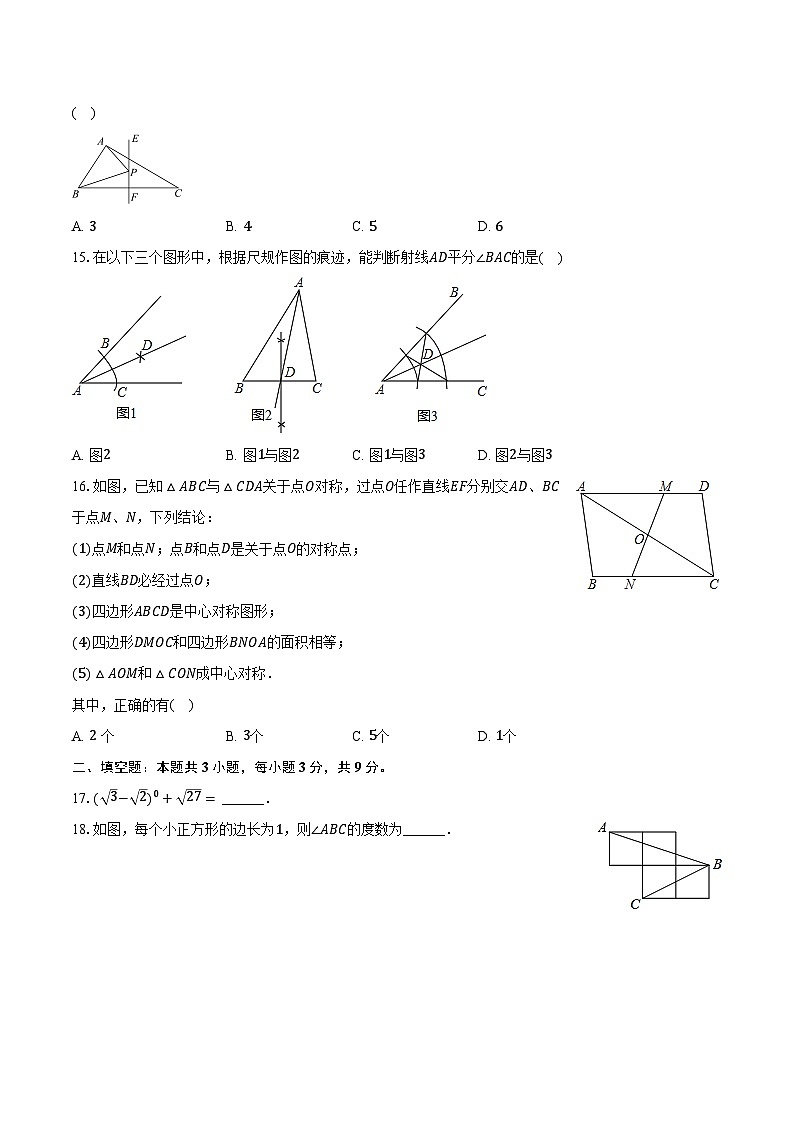
14.如图，在△ABC中，∠BAC=90°，AB=3，AC=4，BC=5，EF垂直平分BC，点P为直线EF上的任一点，则AP+BP的最小值是
( )
A. 3B. 4C. 5D. 6
15.在以下三个图形中，根据尺规作图的痕迹，能判断射线AD平分∠BAC的是( )
A. 图2B. 图1与图2C. 图1与图3D. 图2与图3
16.如图，已知△ABC与△CDA关于点O对称，过点O任作直线EF分别交AD、BC于点M、N，下列结论：
(1)点M和点N；点B和点D是关于点O的对称点；
(2)直线BD必经过点O；
(3)四边形ABCD是中心对称图形；
(4)四边形DMOC和四边形BNOA的面积相等；
(5)△AOM和△CON成中心对称．
其中，正确的有( )
A. 2 个B. 3个C. 5个D. 1个
二、填空题：本题共3小题，每小题3分，共9分。
17.( 3− 2)0+ 27= ______．
18.如图，每个小正方形的边长为1，则∠ABC的度数为______．
19.如图，△ABC中，∠C=90°，AB=10cm，BC=6cm，动点P从点C出发，以每秒2cm的速度按C→A的路径运动，设运动时间为t秒.出发2秒时，AP= ______cm，△ABP的面积为______cm2，t= ______时，BP恰好平分∠ABC．
三、解答题：本题共6小题，共48分。解答应写出文字说明，证明过程或演算步骤。
20.(本小题8分)
先化简，再求值：x2+3xx+3+4x2−12x−1，其中x=1 2+1．
21.(本小题8分)
已知a，b，m都是实数，若a+b=2，则称a与b是关于l的“平衡数”．
(1)4与______是关于l的“平衡数”，3− 2与______是关于l的“平衡数”；
(2)若(m+ 3)(1− 3)=−2，判断m+ 3与2− 3是否是关于l的“平衡数”，并说明理由．
22.(本小题8分)
如图，在△ABC中，AD是BC边上的中线，DE⊥AB于点E，DF⊥AC于点F，且DE=DF．
求证：(1)△BDE≌△CDF；
(2)AD⊥BC．
23.(本小题8分)
(1)如图1，△ABC中，AB≠AC，∠ABC，∠ACB的平分线交于O点，过O点作EF/​/BC交AB，AC于点E，F.图中有______个等腰三角形.猜想：EF与BE，CF之间有怎样的关系，并说明理由；
(2)如图2，若AB=AC，其他条件不变，图中有______个等腰三角形；EF与BE，CF间的关系是______；
(3)如图3，AB≠AC，若∠ABC的角平分线与△ABC外角∠ACD的角平分线交于点O，过点O作OE/​/BC交AB于E，交AC于F.图中有______个等腰三角形.EF与BE，CF间的数量关系是______．
24.(本小题8分)
永州市万达广场筹建之初的一项挖土工程招标时，接到甲、乙两个工程队的投标书，每施工一天，需付甲工程队工程款2.4万元，付乙工程队工程款1.8万元，工程领导小组根据甲、乙两队的投标书测算，可有三种施工方案：
(方案一)甲队单独完成这项工程，刚好按规定工期完成：
(方案二)乙队单独完成这项工程要比规定工期多用6天；
(方案三)若由甲、乙两队合作做5天，剩下的工程由乙队单独做，也正好按规定工期完工．
(1)请你求出完成这项工程的规定时间；
(2)如果你是工程领导小组的组长，为了节省工程款，同时又能如期完工，你将选择哪一种方案？说明理由．
25.(本小题8分)
已知△ABC中，∠A=90°，AB=AC，点D为BC的中点．
(1)如图1，点E、F分别为线段AB、AC上的点，当BE=AF时，易得△DEF为______三角形；
(2)如图2，若点E、F分别为AB、CA延长线上的点，且BE=AF，其他条件不变，则(1)中的结论仍然成立，请证明这个结论；
(3)如图3，若把一块三角尺的直角顶点放在点D处转动，三角尺的两条直角边与线段AB、AC分别交于点E、F，请判断△DEF的形状，并证明你的结论．
答案和解析
1.【答案】A
【解析】解：A、 6是无理数，选项正确；
B、 25=5是整数，是有理数，选项错误；
C、713是分数，是有理数，选项错误；
D、3.1415是有限小数，是有理数，选项错误．
故选：A．
无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．
此题主要考查了无理数的定义，其中初中范围内学习的无理数有：π，2π等；开方开不尽的数；以及像0.1010010001…，等有这样规律的数．
2.【答案】D
【解析】解：由题意得，x+2≥0且x≠0，
解得x≥−2且x≠0．
故选：D．
根据二次根式及分式有意义的条件列出关于x的不等式，求出x的取值范围即可．
本题考查的是二次根式有意义的条件，熟知二次根式中的被开方数是非负数是解题的关键．
3.【答案】B
【解析】【分析】
本题考查了等腰三角形的概念，三角形的三边关系，利用分类讨论思想是解题的关键．
分两种情况讨论，利用三角形的三边关系可求解．
【解答】
解：当第三边为2时，∵2+2=4，
∴长度为2，2，4的三条线段不能构成三角形，
∴第三边为2不合题意；
当第三边为4时，∵2+4>4，
∴长度为2，4，4的三条线段能构成三角形，
∴第三边为4符合题意，
故选：B．
4.【答案】A
【解析】解：A、 14是最简二次根式，故A符合题意；
B、 12=2 3，故B不符合题意；
C、 4=2，故C不符合题意；
D、1 2= 22，故D不符合题意；
故选：A．
根据最简二次根式的定义，逐一判断即可解答．
本题考查了最简二次根式，熟练掌握最简二次根式的定义是解题的关键．
5.【答案】A
【解析】【分析】
本题考查了全等三角形的判定定理的应用，能灵活运用全等三角形的判定定理进行推理是解此题的关键．
根据垂直定义求出∠CFD=∠AEB=90°，再根据全等三角形的判定定理推出即可．
【解答】
解：条件是AB=CD．
理由是：∵AE⊥BC，DF⊥BC，
∴∠CFD=∠AEB=90°，
在Rt△ABE和Rt△DCF中，
AB=CDBE=CF，
∴Rt△ABE≌Rt△DCF(HL)，
故选A．
6.【答案】C
【解析】解：∵在平面内，把一个图形绕着某个点旋转180°，如果旋转后的图形与原图形重合，则这个图形为中心对称图形，
∴C选项中的图形为中心对称图形，
故选：C．
根据在平面内，把一个图形绕着某个点旋转180°，如果旋转后的图形与原图形重合，则这个图形为中心对称图形判断即可．
本题主要考查中心对称图形的知识，熟练掌握中心对称图形的概念是解题的关键．
7.【答案】C
【解析】解：∵2< 5