2023-2024学年湖北省黄石市阳新县八年级（上）期末数学试卷

这是一份2023-2024学年湖北省黄石市阳新县八年级（上）期末数学试卷，共9页。试卷主要包含了下列计算正确的是，下列运算中，错误的是，下列结论等内容，欢迎下载使用。
（考试时间：120分钟， 总分：120分）
注意事项：
1．答卷前，考生务必将自己的姓名、考试号填写在试题卷和答题卡上，并将考试号条形码粘贴在答题卡上的指定位置．
2．选择题每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号，答在试题卷上无效.
3．非选择题（主观题）用0.5毫米的黑色签字笔直接答在答题卡上每题对应的答题区域内，答在试题卷上无效．作图一律用2B铅笔或0.5毫米黑色签字笔．
4．考生必须保持答题卡的整洁，考试结束后，请将答题卡上交．
一、仔细选一选（每小题3分，共30分）
1．剪纸文化是中国最古老的民间艺术之一，下列剪纸图案中，不是轴对称图形的是（ ）
A． B． C． D．
2．（3分）代数式1x，a+b3，3π，5x+y，2m-n4m中，分式有 （ ）
A．4个B．3个C．2个D．1个
3．下列生活中的一些事实运用了“三角形稳定性”的是 （ ）
A．B． C．D．
4．在下列各组线段中，不能构成三角形的是 （ ）
A．5，7，10B．7，10，13C．5，10 13D．5，7，13
5．下列各式中能用平方差公式计算的是 （ ）
A.（-x+2y）（x-2y）B.（1-5m）（5m-1）
C.（3x-5y）（3x+5y）D.（a+b）（-a-b）
6．下列计算正确的是 （ ）
A（x2）3＝x5B.（-3a2b）3＝-27a6b3
C．3a3•2a2＝6a6D.（-x）5÷（-x）2＝x3
7．下列运算中，错误的是 （ ）
A．-a-ba+b=-1 B．0.5a+b0.2a-0.3b=5a+10b2a-3b C．x2-y2x2+2xy+y2=x-yx+y D．m3m2+m=m+m2
8.已知一艘轮船顺水航行46千米和逆水航行34千米共用的时间，正好等于船在静水中航行80千米所用的时间，并且水流的速度是2千米/小时，求设轮船在静水中的速度为x千米/小时，是下列方程正确的是 （ ）
A．46x-2+34x+2=80x B．46x+2+34x-2=80x C．46x-34x-2=80x+2 D．34x+2=80x-2+46x
9题
9．如图，在Rt△ABC中，∠ACB=90°,AC=6,BC=8,AB=10,如果点D，E分别为BC,AB上的动点，那么AD+DE的最小值是 （ ）
A．10.8
B．10
C．9.6
D．8.4
10．下列结论：①不论a为何值时aa2+1都有意义；②a＝-1时，分式a+1a2-1的值为0；③若x2+1x-1的值为负，则x的取值范围是x＜1；④若x+1x+2÷x+1x有意义，则x的取值范围是x≠-1，x≠-2且x≠0．其中正确的是（ ）
A．①②④B．①③④C．①②③D．②③④
二、认真填一填（每小题3分，共18分）
14题
11．清代•袁枚的一首诗《苔》中的诗句：“白日不到处，青春恰自来．苔花如米小，也学牡丹开．”若苔花的花粉直径约为0.0000084米，则数据0.0000084科学记数法表示为 ．
12．分解因式：xy4﹣6xy3+9xy2＝ ．
13．一个n边形的内角和是它外角和的3倍，则边数n＝ ．
14．如图，△ABC的三边AB、BC、CA长分别是20、30、40，其三条
角平分线将△ABC分成三个三角形，则S△ABO：S△BCO：S△CAO等于 ．
15．若关于y的不等式组3y-12≥y+12-15(y-a)＞0无解，且关于x的分式方程xx+1+4a+1x+1=-1的解为负数，则所有满足条件的整数a的值之和是 ．
16题
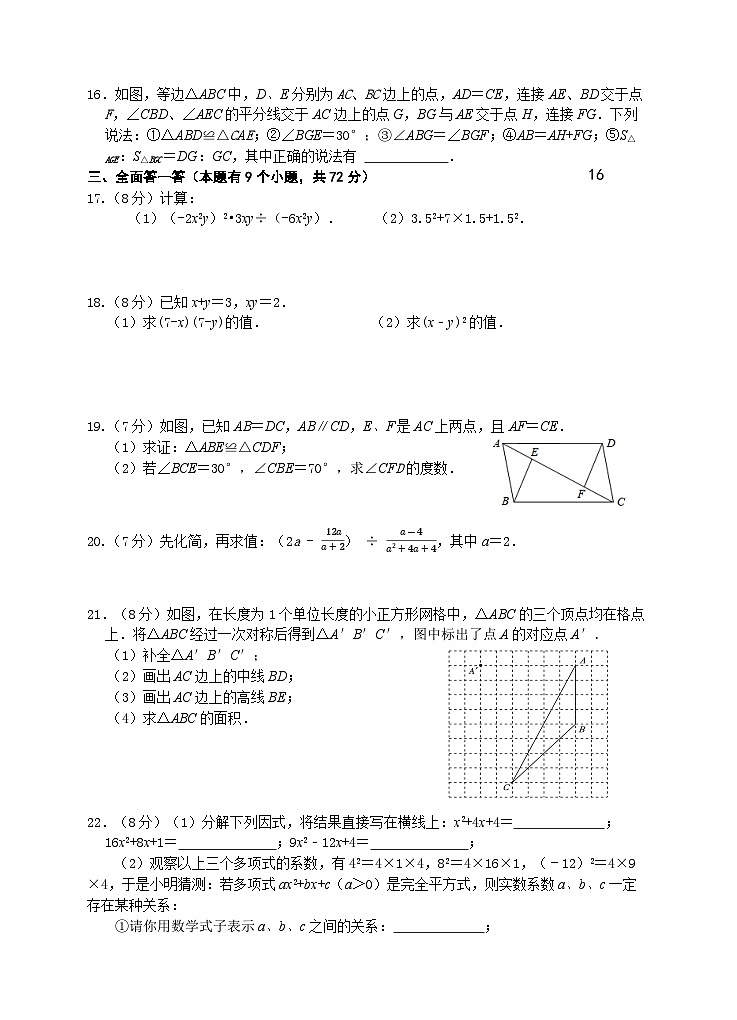
16．如图，等边△ABC中，D、E分别为AC、BC边上的点，AD＝CE，连接AE、BD交于点F，∠CBD、∠AEC的平分线交于AC边上的点G，BG与AE交于点H，连接FG．下列说法：①△ABD≌△CAE；②∠BGE＝30°；③∠ABG＝∠BGF；④AB＝AH+FG；⑤S△AGE：S△BGC＝DG：GC，其中正确的说法有 ．
三、全面答一答（本题有9个小题，共72分）
17.（8分）计算：
（1）（-2x2y）2•3xy÷（-6x2y）． （2）3.52+7×1.5+1.52．
18.（8分）已知x+y＝3，xy＝2．
（1）求(7-x)(7-y)的值． （2）求(x﹣y)2的值．
19.（7分）如图，已知AB＝DC，AB∥CD，E、F是AC上两点，且AF＝CE．
（1）求证：△ABE≌△CDF；
（2）若∠BCE＝30°，∠CBE＝70°，求∠CFD的度数．
20.（7分）先化简，再求值：（2a-12aa+2）÷a-4a2+4a+4，其中a＝2．
21．（8分）如图，在长度为1个单位长度的小正方形网格中，△ABC的三个顶点均在格点上．将△ABC经过一次对称后得到△A′B′C′，图中标出了点A的对应点A′．
（1）补全△A′B′C′；
（2）画出AC边上的中线BD；
（3）画出AC边上的高线BE；
（4）求△ABC的面积．
22．（8分）（1）分解下列因式，将结果直接写在横线上：x2+4x+4＝ ；16x2+8x+1＝ ；9x2﹣12x+4＝ ；
（2）观察以上三个多项式的系数，有42＝4×1×4，82＝4×16×1，（﹣12）2＝4×9×4，于是小明猜测：若多项式ax2+bx+c（a＞0）是完全平方式，则实数系数a、b、c一定存在某种关系：
①请你用数学式子表示a、b、c之间的关系： ；
②解决问题：若多项式x2﹣2（m﹣3）x+（10﹣6m）是一个完全平方式，求m的值．
23.（8分）为丰富同学们的课余生活，培养同学们的创新意识和实践能力，某校七年级举办了“玩转科技、畅想未来”活动，为了表彰活动中表现优秀的同学，学校准备采购A、B两种奖品．这两种奖品在甲、乙两个商场的标价相同，A奖品的单价与B奖品单价之和为35元，买10份A奖品和20份B奖品一共需450元．
（1）求A奖品和B奖品的单价分别是多少？
（2）甲、乙两商场举办让利活动：甲商场所有商品以相同折扣打折销售，乙商场买一份A奖品送一份B奖品．采购时发现在甲商场用200元买的B奖品数量比用200元买的A奖品数量的2倍还多5件．
①甲商场的商品打几折？
②若学校准备采购m件A奖品和n件B奖品，当m，n满足什么数量关系时，在甲、乙两个商场所花费用一样．
24.(8分)在等边△ABC中，点D、E分别是AB、AC上的点，BD＝AE，BE与CD交于点O．
（1）如图1，填空：∠BOD＝ 度；
（2）如图2，以CO为边作等边△OCF，连接AO、BF，那么BF与AO相等吗？并说明理由；
（3）如图3，在（2）的条件下，若点G是BC的中点，连接GO，判断BF与GO有什么数量关系？并说明理由．
25.（10分）在平面直角坐标系中，A（﹣5，0），B（0，5），点C为x轴正半轴上一动点，过点A作AD⊥BC交y轴于点E．
（1）如图①，若C（3，0），求点E的坐标；
（2）如图②，若点C在x轴正半轴上运动，且OC＜5，其它条件不变，连接DO，求证：DO平分∠ADC；
（3）若点C在x轴正半轴上运动，当OC+CD＝AD时，求∠OBC的度数．