河南省新乡市辉县市2023-2024学年下学期九年级期中考试数学试卷

这是一份河南省新乡市辉县市2023-2024学年下学期九年级期中考试数学试卷，共10页。试卷主要包含了04，对于实数a,b,定义运算“★”等内容，欢迎下载使用。


一、选择题(每小题3分,共30分)
1.实数a,b,c,d在数轴上对应点的位置如图所示,这四个数中绝对值最大的是( )

A.a B.b C.c D.d
2.2023年10月,第三届“一带一路”国际合作高峰论坛在北京举行,本次高峰论坛达 成合作远超上届,预计未来5年,中国货物贸易进出口额有望累计超过32万亿美元.其 中“32万亿”用科学记数法表示为( )
A.32×1012 B.3.2×1014 C.32×1013 D.3.2×1013
3.如图,将一直角梯形纸片绕虚线旋转一周形成一个几何体,则该几何体的俯视图( )

A B C D
4.计算1x-1-2x2-1的结果等于( )
A.－1 B.x－1 C.1x+1 D.2x2-1
5.一束光线射向两块平行玻璃板,在玻璃板表面会发生反射和折射,光路如图所示,已知AB//DE, 若∠ABC＝80°, 则∠1的度数为( )
A.40°
B.50°
C.60°
D.70°
6.四边形ABCD是平行四边形,下列结论中错误的是( )
A.当∠ABC＝90°时,□ABCD是矩形
B.当AB＝BC时,□ABCD是菱形
C.当AC⊥BD时,□ABCD是菱形
D.当AC＝BD时,□ABCD是正方形
7.若点A(x1,－2),B(x2,1),C(x3,2)都在反比例函数y＝－2x的图象上,则x1,x2,x3
的大小关系是( )
A.x3＜x2＜x1 B.x2＜x1＜x3 C.x1＜x3＜x2 D.x2＜x3＜x1
8.如图,AB是ʘO的直径,∠BAC＝50°,则∠D＝( )
A.40° B.20° C.80° D.50°
9.对于实数a,b,定义运算“★”：a★b＝a2-b(a≤b)b2-a(a>b),已知关于x的方程x★(x－2)＝m恰好有两个不相等的实数根,则m的取值范围是( )
A.m＜－94 B.m＞－94 C.m＜74 D.m＞74
10.如图(1),在△ABC中,BA＝BC＝5,AC＝6.动点P从点A出发,先沿AC运动到点D,再从点D沿直线运动到点B.设点P运动的路程为x,△ABP的面积为y,图(2)是点P运动时y与x的函数关系图象,则m的值为( )

图(1) 图(2)
A.2 B.2.5 C.3 D.4
二、填空题(每小题3分,共15分)
11.列代数式 .
12.已知关于x、y的方程组2x+y=2a+1x+2y=a-1的解满足x－y＝4,则a的值为 .
中国古代的“四书”是指《论语》《孟子》《大学》《中庸》,它是儒家思想的核心著作,是中国传统文化的重要组成部分.若从这四部著作中随机抽取两本(先随机抽取一本,不放回,再随机抽取另一本),则抽取的两本恰好是《论语》和《大学》的概率是 .
14.如图,在平面直角坐标系中,菱形OABC的顶点A在x轴正半轴上,顶点B 、C在第一象限内,且∠ABC＝60°,AB＝4.若菱形OABC的顶点C在矩形ODBE的边OE上,则点E的坐标为 .
(第14题) (第15题)
15.如图,在等边三角形ABC中,AB＝2,AD为BC边上的高,以AD为边在AD右侧作△ADE,使AE＝AD,当点E恰好落在△ABC的中位线所在的直线上时,DE的长为 .
三、解答题(本大题共8小题,满分75分)
16.(10分)计算:(1)(-1)0+(-2)-1+cs60°
(2)化简:(x＋2y)(－x＋2y)＋(x-2y)2
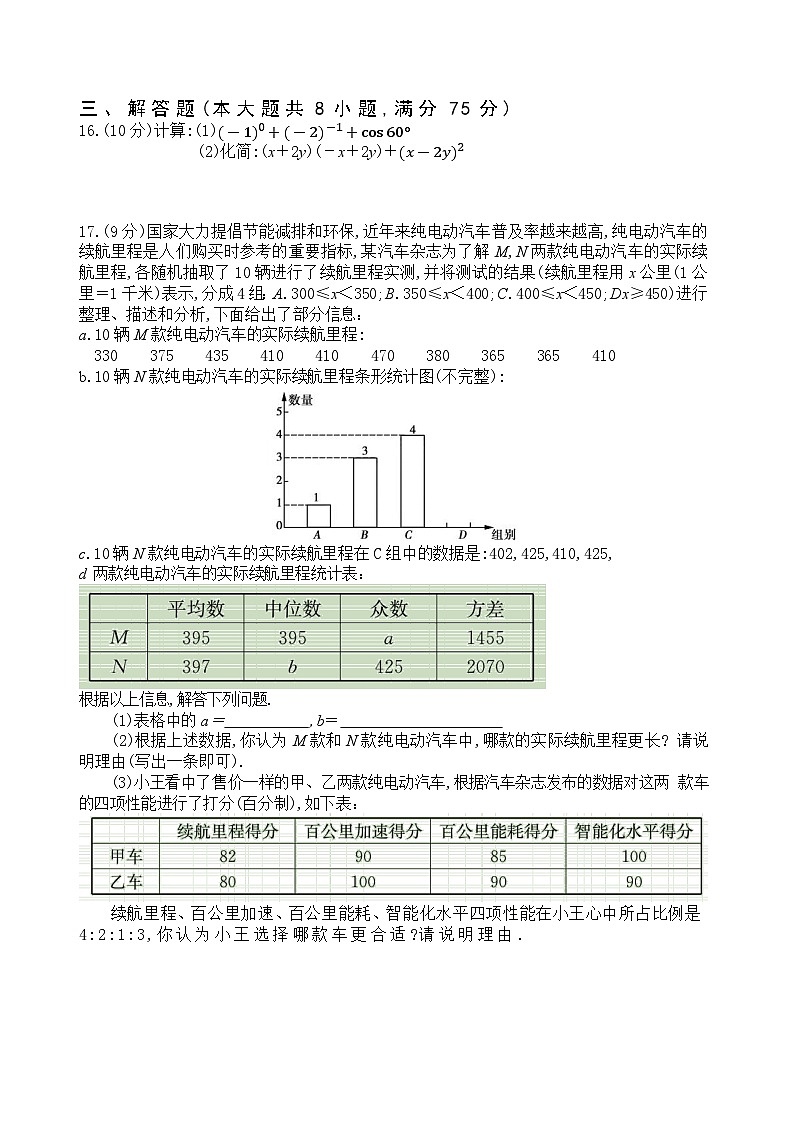
17.(9分)国家大力提倡节能减排和环保,近年来纯电动汽车普及率越来越高,纯电动汽车的续航里程是人们购买时参考的重要指标,某汽车杂志为了解M,N两款纯电动汽车的实际续航里程,各随机抽取了10辆进行了续航里程实测,并将测试的结果(续航里程用x公里(1公里＝1千米)表示,分成4组：A.300≤x＜350;B.350≤x＜400;C.400≤x＜450;Dx≥450)进行整理、描述和分析,下面给出了部分信息：
a.10辆M款纯电动汽车的实际续航里程:
330 375 435 410 410 470 380 365 365 410
b.10辆N款纯电动汽车的实际续航里程条形统计图(不完整):
c.10辆N款纯电动汽车的实际续航里程在C组中的数据是:402,425,410,425,
d 两款纯电动汽车的实际续航里程统计表：
根据以上信息,解答下列问题.
(1)表格中的a＝ ,b＝
(2)根据上述数据,你认为M款和N款纯电动汽车中,哪款的实际续航里程更长? 请说明理由(写出一条即可).
(3)小王看中了售价一样的甲、乙两款纯电动汽车,根据汽车杂志发布的数据对这两 款车的四项性能进行了打分(百分制),如下表：
续航里程、百公里加速、百公里能耗、智能化水平四项性能在小王心中所占比例是4:2:1:3,你认为小王选择哪款车更合适?请说明理由 .
18.(9分)如图,在正方形网格中,△ABC的顶点均在格点上,请仅用无刻度直尺完成下列作图(保留作图痕迹)
(1)在图1中,作△ABC关于点O对称的图形△A1B1C.
(2)在图2中,作出将△ABC绕点A逆时针旋转90°,再向左平移2个单位长度后的图形△A2B2C2 .
(3)在图3中,找一格点P,连接PB,使∠PBC＝45°
19.(9分)如图,小周通过定滑轮O 拉动静止在水平地面上的高为0.5米的长方体重物,开始时与重物相连的绳子和水平面的夹角为37°,拉动 一段距离后,绳子与水平面的夹角为53°,绳子的自由端(用手拉的一端)竖直向下移动了1.5米(绳子伸缩不计),求定滑轮O 到地面的距离(结果精确到1米,参考数据：sin37°≈0.6,cs37°≈0.8,tan37°≈0,75)
20. (9分)甲公司将员工的午餐外包给某家餐饮公司,该餐饮公司根据每天甲公司员工团购订餐的数量,给出以下优惠方案：
(1)某天甲公司有40人团购订餐,且订A套餐的人数不少于25人.若按方案一结算的总费用恰为1060元,求这天订A套餐和B套餐的人数分别有多少人.
(2)某天甲公司有60人团购订餐,其中订B套餐的人数大于订A套餐人数的2倍,设其中有x人 订A套餐,按方案一结算的总费用为y1元,按方案二结算的总费用为 y2 元 .
①分别求y1,y2与 x之间的函数关系式.
②若按方案二结算较合算,则x的值为
21. (9分)小明在玩一个直径为60cm 的塑料圆环玩具,我们将其看成⨀O,在水平地面上有一个坡角为60°的斜坡AB.
(1)如图(1),当塑料圆环⨀O与水平地面的接触点C距离斜坡AB的底端A点103cm时,塑料圆环与斜坡AB是否相切?为什么?
(2)如图(2),小明将塑料圆环⊙O滚到了斜坡 AB上,设⨀O与斜坡AB的接触点 为D,当点D距离水平地面20cm ( 即DE＝20cm)时,塑料圆环的最低点距离水平地面多高?
22.(10分)在数学实践活动课上,小明在白纸上画了一条形状与抛物线y＝－ x² 相 同的抛物线L,并在一张透明胶片上画了一个平面直角坐标系,在坐标系中画了线段DE( 点D,E 的坐标分别为(2,4),(5,4)).小明将胶片覆盖在白纸上,使抛物线L的对称轴与直线x＝2重合,抛物线L与 y轴交于点C(0,－2),如图,
(1)求此时抛物线L的表达式.
(2)保持纸片不动,将胶片先向左平移1个单位长度,再向下平移m 个单位长度.
①平移后,抛物线L 的顶点坐标为 (用含m代数式表示)
②若平移后,抛物线L 与线段DE有且只有一个交点,求m 的取值范围.
23.(10分)综合与实践
综合与实践课上,数学兴趣小组对图形中两条互相垂直的线段间的数量关系进行了探究.
(1)操作判断
①如图(1),在正方形ABCD中,点E,F,G,H分别在边 AB,CD,AD,BC上,且EF⊥GH,若 EF＝5,则 GH的长为
②如图(2),在矩形 ABCD中 ,BC＝2AB,点 E,F,G,H分别在边AB,CD,AD, BC 上,且EF⊥GH,若 EF＝8,则 GH的长为
(2)迁移探究
如图(3),在Rt△ABC中,∠BAC＝90°,AB＝AC,点 D,E分别在边AC,BC上 ,且AE⊥BD,试证明ABAD=BEEC
(3)拓展应用
如图(4),在矩形ABCD中,AB＝6,BC＝10,BE平分∠ABC交 AD于点E,点F为 AE上 一 点,AG⊥BF交 BE于点H,交 矩 形ABCD的边于点G,当 F 为 AE的 三等分点时,请直接写出 AG 的长.
九年级下期期中数学试卷参考答案
2024.04
一、选择题(每小题3分，共30分)
1.A 2.D 3.B 4.C 5.B 6.D 7.D 8.A 9.B 10.C
二、填空题(每小题3分，共15分)
11.2m+3n 12.2 13.16 14.(3,33) 15.3或3
三、解答题(本大题共8个小题，满分75分)
16.(1)解:原式＝1－12＋12＝1
(2)解:原式＝4y2－x2＋x2－4xy＋4y2＝8y2－4xy
17.(1)410 406
(2)N款的实际续航里程更长.理由:∵N 款的平均数较大.∴N 款实际续航里程更长.
(3)选择甲款车.理由:甲款车综合得分为82×410＋90×210＋85×110＋100×310＝89.3(分)
乙款车综合得分为80×410＋100×210＋90×110＋90×310＝88(分)
∵89.3＞88 ∴选择甲款车更合适.
18.解:(1)如图1所示,△A₁B₁C₁即为所求.(2)如图2所示,△A₂B₂C₂即为所求.(3)如图3所示,点P即为所求.
19.解:如图由题意得OA－OB＝1.5m,设OB＝x米,则OA＝(x＋1.5)米
在Rt△AOC中,∠ACO＝90°,∠OAC＝37°
∴sin37°＝OCOA ∴OC＝OA·sin37°≈0.6(x＋1.5)＝(0.6x＋0.9)米
在Rt△OBC中,∠BCO=90°,∠OBC=53°
∴∠BOC=90°－53°＝37° ∴cs37°＝OCOB
∴OC＝OB·cs37°≈0.8x(米)
∴0.6x＋0.9＝0.8x x＝4.5
∴OC＝0.8×4.5＝3.6(米)
∴3.6＋0.5≈4(米)
答:定滑轮O到地面的距离约为4米.
20.解:设这天订A套餐的人数有a人,订B套餐的人数有b人.
∵a＋b＝40,a≥25,∴b≤15.
根据题意,得a+b=40,30×0.9a+25b=1060.
解得a=30,b=10.
答:这天订A套餐和B套餐的人数分别有30人,10人.
(2)①由题意可知,60－x＞2x,
解得x＜20,
则y1＝30x＋25×0.8(60－x)＝10x＋1200.
若60人均订B套餐,则优惠前的总费用为1500元,超过1000元,
从而可知y2＝30x＋25(60－x)－220＝5x＋1280.
②17,18或19
解法提示:由题意可知,y1＞y2,
∴10x＋1200＞5x＋1280,
解得x＞16, ∴16＜x＜20,
∴x的值为17,18或19.
21.解:(1)相切.
理由:如图(1),连接OC,过点O作AB的垂线,垂足为P,连接OA.
∵⊙O与水平地面相切于点C,
∴OC⊥CA,
∵tan∠OAC=OCAC=30103=3,
∴∠OAC＝60°,∴∠OAP＝180°－60°×2＝60°＝∠OAC.
又OA＝OA,∠OCA＝∠OPA,
∴△OCA≌△OPA,
∴OP＝OC,
即OP是⊙O的半径,
∴塑料圆环⊙O与斜坡 AB相切.
(2)如图(2),过点O向水平地面作垂线,垂足为点G.与⊙O交于点F,则FG即为所求.连接OD并延长,与水平地面交于点M.
∵⊙O与斜坡AB相切于点D,
∴OM⊥AB,
∵∠BAM=60°,∠AMD=30°.
又∵DE⊥AM,
∴DM =2DE =40.
∵DE⊥AM,OG⊥AM,∴DE//OG,
∴△DEM∽△OGM,
∴DEOG=DMOM,即20OG=4070,
∴OG＝35.
22.解:(1)∵抛物线L的对称轴与直线x=2重合,
∴抛物线L的顶点横坐标为2
∵抛物线L与y＝－x2的形状相同.
∴设解析式为y＝－(x－2)2＋h,把C(0,－2)代入得,
－2＝－4＋h,∴h＝2
∴y＝－(x－2)2＋2
(2)①(3,2＋m)
②第一种情况:当抛物线L的顶点落在线段DE上时,如图(1)则2＋m＝4,
解得m＝2.
第二种情况:当抛物线L经过点D时,如图(2),此时抛物线L与线段DE有两个点,
将D(2,4)代入y＝－(x－3)2＋2＋m,得4＝－1＋2＋m,解得m＝3.
第三种情况:当抛物线L经过点E时,如图(3),此时抛物线L与线段DE只有一个交点,
将E(5,4)代入y＝－(x－3)2＋2＋m,得4＝－4＋2＋m,解得m＝6.
分析可知,当m＝2或3＜m≤6时,抛物线L与线段DE有且只有一个交点.
23.解:(1)①5 ②4
(2)证明:如图(3),过点C作CF⊥AC交AE的延长线于点F.
∵∠F＋∠FAC＝90°＝∠ADB＋∠FAC
∴∠F＝∠ADB
又∵∠BAD＝∠ACF＝90°,BA＝AC
∴△ABD≌△CAF,∴AD＝CF,
易得AB∥CF,∴△ABE∽△FCE,
∴ABCF=BEEC. 又∵CF＝AD,∴ABAD=BEEC.
(3)10103或313