
北京版五年级下册整理与复习课堂检测
展开一、填空题(每空1分,共24分)
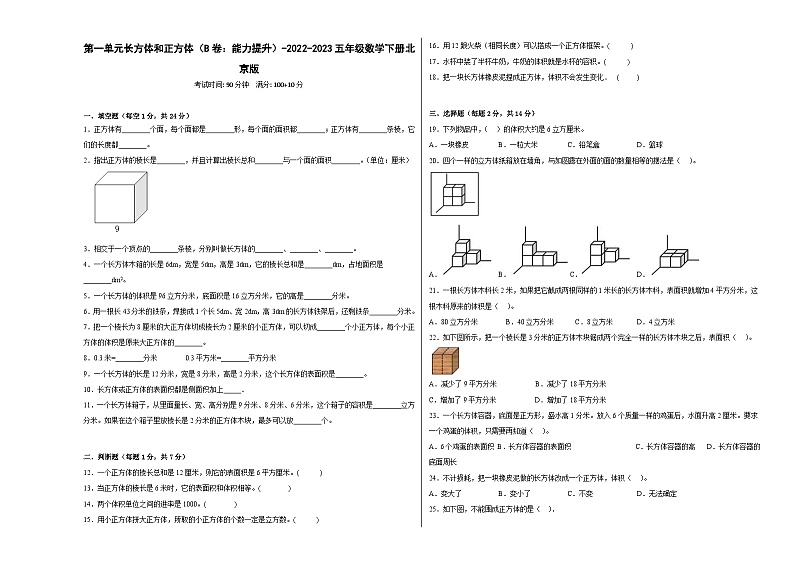
1.正方体有________个面,每个面都是________形,每个面的面积都________;正方体有________条棱,它们的长度都________。
2.指出正方体的棱长是________,并且计算出棱长总和________与一个面的面积________。(单位:厘米)
3.相交于一个顶点的________条棱,分别叫做长方体的________、________、________。
4.一个长方体木箱的长是6dm,宽是5dm,高是3dm,它的棱长总和是________dm,占地面积是________dm2。
5.一个长方体的体积是96立方分米,底面积是16立方分米,它的高是________分米。
6.用一根长43分米的铁条,焊接成1个长5dm、宽2dm,高3dm的长方体铁架后,还剩铁条________分米。
7.把一个棱长为8厘米的大正方体切成棱长为2厘米的小正方体,可以切成________个小正方体,每个小正方体的体积是原来大正方体的________。
8.0.3米=________分米 0.3平方米=________平方分米
9.一个长方体的长是12分米,宽是8分米,高是2分米,这个长方体的表面积是________。
10.长方体或正方体的表面积都是侧面积加上_____.
11.一个长方体箱子,从里面量长、宽、高分别是9分米、8分米、6分米,这个箱子的容积是________立方分米。如果在这个箱子里放棱长是2分米的正方体木块,最多可以放________个。
二、判断题(每题1分,共7分)
12.一个正方体的棱长总和是12厘米,则它的表面积是6平方厘米。( )
13.当正方体的棱长是6米时,它的表面积和体积相等。( )
14.两个体积单位之间的进率是1000。( )
15.用小正方体拼大正方体,所取的小正方体的个数一定是立方数。( )
16.用12跟火柴(相同长度)可以搭成一个正方体框架。( )
17.水杯中装了半杯牛奶,牛奶的体积就是水杯的容积。( )
18.把一块长方体橡皮泥捏成正方体,体积不会发生变化. ( )
三、选择题(每题2分,共14分)
19.下列物品中,( )的体积大约是6立方厘米。
A.一块橡皮B.一粒大米C.铅笔盒D.篮球
20.四个一样的立方体纸箱放在墙角,与如图露在外面的面的数量相等的摆法是( )。
A.B.C.D.
21.一根长方体木料长2米,如果把它截成两根同样的1米长的长方体木料,表面积就增加4平方分米,这根木料原来的体积是( )。
A.80立方分米 B.40立方分米 C.8立方米D.4立方米
22.如下图所示,把一个棱长是3分米的正方体木块锯成两个完全一样的长方体木块之后,表面积( )。
A.减少了9平方分米 B.减少了18平方分米
C.增加了9平方分米 D.增加了18平方分米
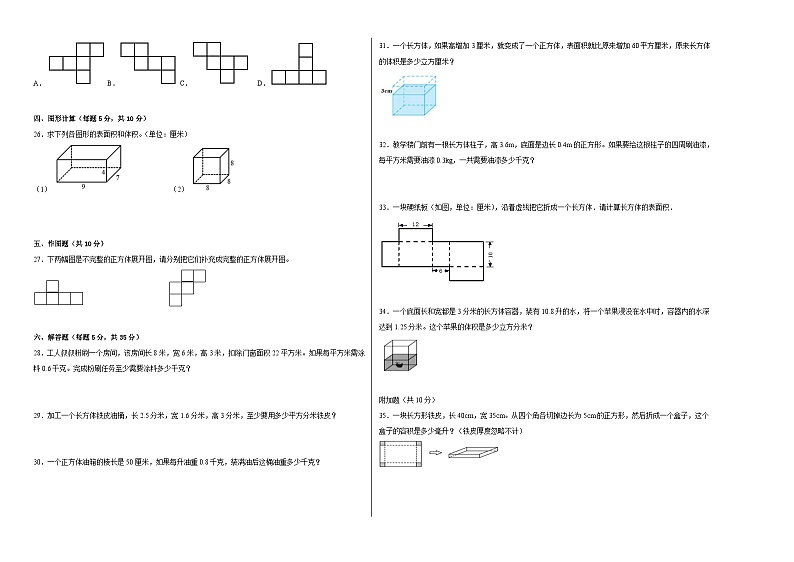
23.一个长方体容器,底面是正方形,盛水高1分米。放入6个质量一样的鸡蛋后,水面升高2厘米。要求一个鸡蛋的体积,只需要再知道( )。
A.6个鸡蛋的表面积B.长方体容器的表面积C.长方体容器的高D.长方体容器的底面周长
24.不计损耗,把一块橡皮泥做的长方体改成一个正方体,体积( )。
A.变大了B.变小了C.不变D.无法确定
25.如下图,不能围成正方体的是( ).
A.B.C.D.
四、图形计算(每题5分,共10分)
26.求下列各图形的表面积和体积。(单位:厘米)
(1) (2)
五、作图题(共10分)
27.下两幅图是不完整的正方体展开图,请分别把它们补充成完整的正方体展开图。
六、解答题(每题5分,共35分)
28.工人叔叔粉刷一个房间,该房间长8米,宽6米,高3米,扣除门窗面积22平方米。如果每平方米需涂料0.6千克。完成粉刷任务至少需要涂料多少千克?
29.加工一个长方体铁皮油桶,长2.5分米,宽1.6分米,高3分米,至少要用多少平方分米铁皮?
30.一个正方体油箱的棱长是50厘米,如果每升油重0.8千克,装满油后这桶油重多少千克?
31.一个长方体,如果高增加3厘米,就变成了一个正方体,表面积就比原来增加60平方厘米,原来长方体的体积是多少立方厘米?
32.教学楼门前有一根长方体柱子,高3.6m,底面是边长0.4m的正方形。如果要给这根柱子的四周刷油漆,每平方米需要油漆0.3kg,一共需要油漆多少千克?
33.一块硬纸板(如图,单位:厘米),沿着虚线把它折成一个长方体.请计算长方体的表面积.
34.一个底面长和宽都是3分米的长方体容器,装有10.8升的水,将一个苹果浸没在水中时,容器内的水深达到1.25分米。这个苹果的体积是多少立方分米?
附加题(共10分)
35.一块长方形铁皮,长40cm,宽35cm。从四个角各切掉边长为5cm的正方形,然后折成一个盒子,这个盒子的容积是多少毫升?(铁皮厚度忽略不计)
参考答案:
1. 6 正方 相等 12 相等
【分析】根据正方体的特征,正方体的6个面都是正方形,每个面的面积都相等,12条棱的长度都相等,据此解答。
【详解】正方体有6个面,每个面都是正方形,每个面的面积都相等。
故答案为:6、正方形、相等、12、相等。
【点睛】本题考查正方体的特征,要根据正方体的立体图形进行记忆。
2. 9厘米 108厘米 81平方厘米
【详解】观察图可知,图中正方体的棱长是9厘米,棱长总和:12×9=108(厘米),一个面的面积:9×9=81(平方厘米)
3. 3 长 宽 高
4. 56 30
【分析】长方体的棱长总和=(长+宽+高)×4;占地面积=长×宽。据此计算。
【详解】棱长总和:(6+5+3)×4
=14×4
=56(分米)
占地面积:6×5=30(平方分米)
【点睛】此题考查的是长方体的棱长总和、面积的计算公式,学生应该熟练掌握。
5.6
【分析】长方体体积=长×宽×高,在长方体中底面积=长×宽,所以长方体的体积公式也可以写成:长方体体积=底面积×高,据此求解。
【详解】96÷16=6(分米),所以这个长方体的高是6分米。
【点睛】本题考查对长方体体积公式的应用。
6.3
【分析】由题意可知:焊接成长方体铁架用的铁条长度是长方体的棱长之和,将数据带入长方体棱长公式求出棱长和,再用总长-棱长和即可求出剩下的长度。
【详解】43-(5+2+3)×4
=43-10×4
=43-40
=3(分米)
【点睛】本题主要考查长方体有关棱长的应用,牢记公式是解题的关键。
7. 64 SKIPIF 1 < 0
【分析】先求出大正方体的体积,再求出小正方体的体积,然后用大正方体的体积除以小正方体的体积,就可以求出切的个数,用小正方体的体积除以大正方体的体积,即为每个小正方体的体积占大正方体体积的几分之几。
【详解】大正方体的体积:8×8×8=512(立方厘米)
小正方体的体积:2×2×2=8(立方厘米)
512÷8=64(个),8÷512= SKIPIF 1 < 0
【点睛】此题考查了正方体的体积公式的灵活应用,需要牢记公式。
8. 3 30
【分析】大单位化为小单位,乘以进率;小单位化大单位,除以进率.
【详解】0.3×10=3(分米)
0.3×100=30(平方分米)
故答案为3、30
9.272平方分米
【分析】长方体表面积=(长×宽+长×高+宽×高)×2,由此根据公式计算表面积即可。
【详解】(12×8+12×2+8×2)×2
=(96+24+16)×2
=136×2
=272(平方分米)
10.两个底面积
【详解】试题分析:根据长方体、正方体的表面积的意义,围成长方体或正方体的6个面的总面积叫做它们表面积;而前后左右四个面是侧面积,上下面是底面积;据此解答.
解:长方体或正方体的表面积都是侧面积加上两个底面积.
故答案为两个底面积.
【点评】此题考查的目的是使学生理解掌握长方体、正方体的表面积的意义.
11. 432 48
【分析】长方体的体积=长×宽×高;
先用除法看看长方体的长、宽、高分别能放几个棱长,然后把它们相乘求积即可。
【详解】9×8×6=432(立方分米);
9÷2=4……1;8÷2=4;6÷2=3;
4×4×3=48(个)
【点睛】此题考查长方体的体积计算公式的运用,注意第二问不要用容积除以每块的体积解决问题。
12.√
【分析】正方体有12条同样长的棱。
【详解】12÷12=1(厘米),1×1×6=6(平方厘米)。所以:正确。
【点睛】此题先求出棱长,根据公式:表面积=棱长×棱长×6计算结果。
13.×
【详解】正方体表面积是表面6个面的面积之和,正方体的体积是所占空间的大小,表面积和体积的意义不同,无法比较大小。
14.×
【详解】相邻两个体积单位之间的进率是1000,题目中没有说相邻,比如1m³=1000000cm³,它们之间的进率是1000000,原题说法错误。
故答案为:×。
15.√
【详解】
大正方体需要小正方体的个数有23、33、43、……,所以用小正方体拼大正方体,所取的小正方体的个数一定是立方数。
16.√
【分析】根据正方体的特征:正方体有6个面,每个面都是正方形,6个面的面积都相等,12条棱的长度都相等,有8个顶点。
【详解】因为正方体的12条棱的长度都相等,
所以用12跟火柴(相同长度)可以搭成一个正方体框架。
故答案为:√
【点睛】本题考查了正方体的特征,12条棱的长度都相等,正方体可以看作特殊的长方体。
17.×
【分析】箱子、油桶、仓库等所能容纳物体的体积,通常叫做它们的容积,因为水杯里的牛奶没有装满,所以牛奶的体积小于水杯的容积,据此判断。
【详解】水杯中装了半杯牛奶,牛奶的体积小于水杯的容积,原题说法错误。
故答案为×。
18.√
19.A
【分析】常用的体积单位有立方米、立方分米、立方厘米、立方毫米,根据单位间的进率和联系生活实际、计量单位和数据的大小选择即可。
【详解】一块橡皮的体积大约是6立方厘米。
故选:A。
【点睛】本题考查了体积单位的认识,掌握体积单位的意义可解答问题。
20.D
【分析】分别从正面、右面、后面和上面数出露在外面的面的数量,然后相加即可。
【详解】题干图有:2+4+2=8(个)
图A:3+3+3=9(个)
图B:3+4+2=9(个)
图C:3+3+3+1=10(个)
图D:4+2+2=8(个)
所以,与如图露在外面的面的数量相等的摆法是D。
故选:D。
【点睛】组合图形的计数实质上就是分类计数图形,要按顺序分类计数,防止遗漏。
21.B
【分析】将长方体木料截成两根,表面积增加了两个横截面,求出一个截面面积×长即可。
【详解】2米=20分米
4÷2×20=40(立方分米)
故答案为:B
【点睛】关键是灵活运用长方体体积公式,长方体体积=长×宽×高=底面积×高=横截面×长。
22.D
【分析】根据正方体的特征,它的6个面都是正方形,6个面的面积都相等;把一个棱长是3分米的正方体木块锯成两个完全一样的长方体木块之后,表面积增加两个截面的面积;根据正方形的面积公式解答。
【详解】表面积增加:
3×3×2
=9×2
=18(平方分米)
故答案为:D
【点睛】此题主要考查正方体的特征和表面积的计算方法,关键是明确把一个正方体木块锯成两个完全一样的长方体木块之后,表面积增加两个截面的面积。
23.D
【详解】此题主要考查了不规则物体的体积计算,根据题意,鸡蛋放入水中后 ,水面上升,上升部分的体积就是这些鸡蛋的体积,所以只需要再知道长方体容器的底面周长,这个长方体容器的底面是正方形,据此就可以求出正方形的边长,然后求出底面积,从而求出鸡蛋的体积,据此解答。
24.C
25.D
【分析】此题主要考查了正方体展开图形状规律,注意记忆只要有“田”字格的展开图都不是正方体的表面展开图是解决问题的关键.
【详解】不能围成正方体的是D.
故答案为D.
26.(1)254平方厘米;252立方厘米
(2)384平方厘米;512立方厘米
【分析】(1)把长方体的长、宽、高的数据代入长方体的表面积公式:S=(a×b+a×h+b×h)×2,和长方体的体积公式:V=a×b×h中,计算出长方体的表面积和体积。
(2)把正方体棱长的数据代入正方体的表面积公式:S=6a2,和正方体的体积公式:V=a3中,计算出正方体的表面积和体积。
【详解】(1) SKIPIF 1 < 0
= SKIPIF 1 < 0
= SKIPIF 1 < 0
SKIPIF 1 < 0 (平方厘米)
SKIPIF 1 < 0 SKIPIF 1 < 0 (立方厘米)
即长方体的表面积是254平方厘米,体积是252立方厘米。
(2) SKIPIF 1 < 0 SKIPIF 1 < 0 (平方厘米)
SKIPIF 1 < 0 SKIPIF 1 < 0 (立方厘米)
即正方体的表面积是384平方厘米,体积是512立方厘米。
27.
【详解】根据正方体展开图的11种特征,左图在四个正方形的下面添上一个正方形,即成为正方体展开图的“141”结构,就是一个完整的正方体展开图;
右图在下行左边添上一个正方形,即成为正方体展开图的“222”结构,就是一个完整的正方体展开图。
【点睛】本题是考查正方体的展开图,培养学生的观察能力和空间想象能力。
28.66千克
【分析】根据题意可知,要求粉刷面积,用长×宽+(长×高+宽×高)×2-门窗的面积=需要粉刷的面积,然后用每平方米需要涂料的质量×需要粉刷的面积=一共需要涂料多少千克,据此列式解答。
【详解】8×6+(8×3+6×3)×2
=48+(24+18)×2
=48+42×2
=48+84
=132(平方米)
132-22=110(平方米)
110×0.6=66(千克)
答:完成粉刷任务至少需要涂料66千克。
【点睛】注意粉刷室内墙面时,底面一般不粉刷,所以只求5个面的面积即可。
29.32.6平方分米
【分析】长方体的表面积=(长×宽+长×高+宽×高)×2,据此列式解答。
【详解】(2.5×1.6+2.5×3+1.6×3)×2
=(4+7.5+4.8)×2
=16.3×2
=32.6(平方分米)
答:至少要用32.6平方分米铁皮。
【点睛】本题考查了长方体的表面积,油桶一般是密封的,所以有6个面。
30.100千克
【解析】根据公式:正方体容积=棱长×棱长×棱长,求出油的体积,如果每升油重0.8千克,油的体积乘0.8即油的重量。
【详解】50×50×50=125000(立方厘米)
125000立方厘米=125立方分米=125升
125×0.8=100(千克)
答:装满油后这桶油重100千克。
【点睛】灵活运用正方体容积公式,并注意单位的统一是解决此题的关键。
31.50立方厘米
【解析】根据题意可知,一个长方体如果高增加3厘米,就变成了一个正方体;说明长和宽相等且比高大3厘米,因此增加的60平方厘米是4个同样的长方形的面积和;由此可以求长方体的长=(60÷4)÷3=5厘米,由于长比高多2厘米,那么高=5-3=2厘米,由此解答。
【详解】增加的1个面的面积:60÷4=15(平方厘米)
长方体的长(宽):15÷3=5(厘米)
长方体的高:5-3=2(厘米)
体积:5×5×2=50(立方厘米)
答:原来长方体的体积是50立方厘米。
【点睛】理解增加的60平方厘米是4个同样的长方形的面积和,并知道长方体的体积公式是解决此题的关键。
32.1.728千克
【分析】当长方体的底面是正方形时,则其前后面和左右面完全相同,用3.6×0.4求出一个面的面积,再乘4即可求出前后左右四个面的面积,再乘每平方米需要油漆的质量即可。
【详解】3.6×0.4×4×0.3
=5.76×0.3
=1.728(千克);
答:一共需要油漆1.728千克。
【点睛】本题较易,关键是先求出前后左右四个面的面积和。
33. SKIPIF 1 < 0
34.0.45立方分米
【分析】根据长方体体积公式:V=abh,计算出放入苹果后水的体积,然后减掉放入前的体积,就是苹果的体积。
【详解】10.8升=10.8立方分米
3×3×1.25﹣10.8
=11.25﹣10.8
=0.45(立方分米)
答:这个苹果的体积是0.45立方分米。
【点睛】本题是求不规则物体的体积,可以利用排水法或下降法来求。题目给了3个数据,要把这3个数据合理安排,放在恰当的位置进行计算。
35.3750毫升
【分析】折成的这个长方体的高是5厘米,长是30厘米,宽是25厘米。据此利用长方体的体积公式,直接列式计算出这个盒子的容积即可。
【详解】(40-5×2)×(35-5×2)×5
=30×25×5
=3750(立方厘米)
3750立方厘米=3750毫升
答:这个盒子的容积是3750毫升。
【点睛】本题考查了长方体的体积,长方体的体积等于长乘宽乘高。
小学数学北京版五年级下册五 分数的加法和减法整理与复习课堂检测: 这是一份小学数学北京版五年级下册<a href="/sx/tb_c4048001_t7/?tag_id=28" target="_blank">五 分数的加法和减法整理与复习课堂检测</a>,共15页。试卷主要包含了填空题,判断题,选择题,计算题,解答题等内容,欢迎下载使用。
小学数学北京版五年级下册整理与复习同步达标检测题: 这是一份小学数学北京版五年级下册<a href="/sx/tb_c4048000_t7/?tag_id=28" target="_blank">整理与复习同步达标检测题</a>,共11页。试卷主要包含了填空题,判断题,选择题,计算题,解答题等内容,欢迎下载使用。
北京版五年级下册整理与复习测试题: 这是一份北京版五年级下册<a href="/sx/tb_c4047999_t7/?tag_id=28" target="_blank">整理与复习测试题</a>,共11页。试卷主要包含了填空题,判断题,选择题,解答题等内容,欢迎下载使用。














