2023-2024学年山东省青岛市莱西市七年级(上)期中数学试卷（解析版）

这是一份2023-2024学年山东省青岛市莱西市七年级(上)期中数学试卷（解析版），共15页。试卷主要包含了选择题，填空题，作图题，解答题等内容，欢迎下载使用。
一、选择题（本题满分24分，共8道小题，每小题3分.）
1. 第19届亚运会在浙江杭州举行，下列与杭州亚运会相关的图案中，是轴对称图形的是（ ）
A. B.
C. D.
【答案】D
【解析】A，B，C选项中的图形都不能找到一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以不是轴对称图形；
D选项中的图形能找到一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以是轴对称图形.
故选：D．
2. 若一个三角形的两边长分别为，，则它的第三边的长可能是（ ）
A. B. C. D.
【答案】C
【解析】设第三边长为，根据三角形的三边关系可得：，
解得：.
故选：C．
3. 在中，，，则（ ）
A. B. C. D.
【答案】B
【解析】在中，，
又∵，，∴.
故选：B.
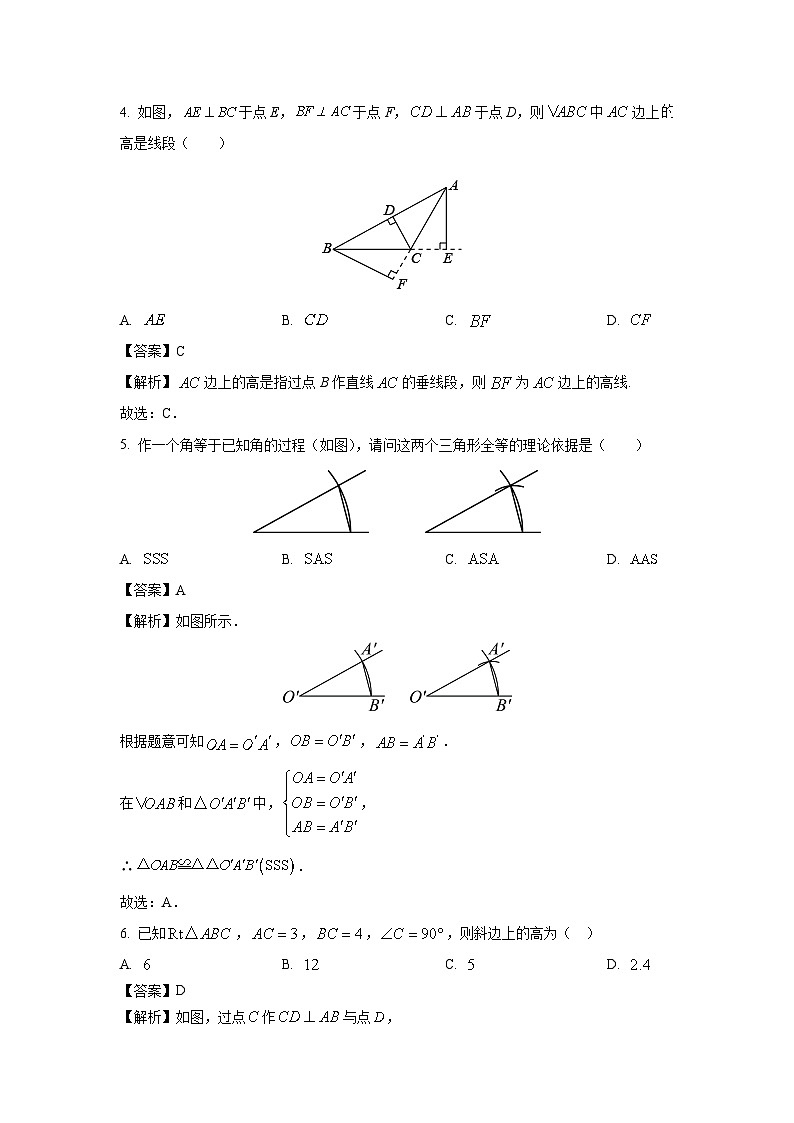
4. 如图，于点E，于点F，于点D，则中边上高是线段（ ）
A. B. C. D.
【答案】C
【解析】边上的高是指过点B作直线的垂线段，则为边上的高线.
故选：C．
5. 作一个角等于已知角的过程（如图），请问这两个三角形全等的理论依据是（ ）
A. B. C. D.
【答案】A
【解析】如图所示．
根据题意可知，，．
在和中，，
∴．
故选：A．
6. 已知，，，，则斜边上的高为（ ）
A. B. C. D.
【答案】D
【解析】如图，过点作与点，
，，，，
，，．
故选：．
7. 如图，在和中，点A、E、B、D在同一条直线上，，，只添加一个条件不能判断的是（ ）
A. B.
C. D.
【答案】C
【解析】∵，∴，
A、∵，，∴，即；
∵，，，
∴，故该选项不符合题意；
B、∵，，，
∴，故该选项不符合题意；
C、∵，，，
不能得到与全等，故该选项符合题意；
D、∵，，∴，
∵，，，
∴，故该选项不符合题意.
故选：C．
8. 如图，，且．、是上两点，，．若，，，则的长为（ ）
A. B. C. D.
【答案】D
【解析】，，，，
，，，
，，，，
，.
故选：．
二、填空题（本题满分24分，共8道小题，每小题3分.）
9. 我们知道圆、线段都是轴对称图形，请再写出一个是轴对称图形的几何图形名称___________．
【答案】正方形（答案不唯一）
【解析】写出一个是轴对称图形的几何图形，如正方形（答案不唯一）．
10. 在中，，则__________．
【答案】70°
【解析】∵AB＝AC，∠A＝40°，∴∠B＝∠C＝70°.
11. 如图，在中，，，，的垂直平分线交于点，交于点，则的周长为_____．
【答案】13
【解析】是的垂直平分线，，
则的周长，
，，的周长.
12. 如图，在中，是的平分线，于点，且，，则的面积为______.
【答案】
【解析】过点作于点，
∵是的平分线，，∴，
∴的面积为.
13. 如图，已知，是的平分线，若，则______.
【答案】
【解析】∵，∴
∵是的平分线，∴，∴，∴，
∵，∴.
14. 如图，在等边三角形中，，是边上的高，延长至点E，使，则的长为______．
【答案】9
【解析】∵是等边三角形，，∴，
∵，∴，∴．
15 小明从家出发向正东方向走了240m，接着向正北方向走了320m，此时小明离家________m．
【答案】400
【解析】如图所示：由题意可得，AO=240m，AB=320m，
故在Rt△OAB中，，
故小明离家400m．
16. 长方体的长为，宽为，高为，点B离点C，一只蚂蚁如果要沿着长方体的表面从点A爬到点B去吃一滴蜜糖，需要爬行的最短距离是______．
【答案】
【解析】只要把长方体的右侧表面剪开与前面这个侧面所在的平面形成一个长方形，如图1：
长方体的宽为，高为，点离点的距离是，
，，
在直角三角形中，根据勾股定理得：
；
只要把长方体的右侧表面剪开与上面这个侧面所在的平面形成一个长方形，如图2：
长方体的宽为，高为，点离点的距离是，
，，
在直角三角形中，根据勾股定理得：
；
只要把长方体的上表面剪开与后面这个侧面所在的平面形成一个长方形，如图3：
长方体的宽为，高为，点离点的距离是，
，
在直角三角形中，根据勾股定理得：；
，
蚂蚁爬行的最短距离是．
三、作图题（本题满分4分.）
17. 尺规作图，不写作法，保留作图痕迹.
已知：线段a和∠α
求作：△ABC，使得AB=a，BC=2a，∠ABC=∠α.
解：如图，先作∠B=∠α，分别在∠B的两边上截取BA=a，BC=2a，
连接AC，则△ABC即为所求作．
四、解答题（本题满分68分，共8小题.）
18. 如图，在长度为1个单位长度的小正方形组成的正方形网格中，点、、在小正方形的顶点上．
（1）在图中画出与关于直线成轴对称的．
（2）在直线上找一点，使的长最短．
解：（1）如图，△即为所求．
（2）如图，点即为所求．
19. 已知：如图，，，，与全等吗？请说明理由．
解：，理由如下：
，，即，
在和中，，．
20. 如图，点在线段上，且，，，连接、，吗？为什么？
解：，理由如下：
，，即，
，，
在和中，
，，．
21. 如图，在中，，是边上的中线．
（1）求证：是等腰三角形；
（2）若的周长为33，，求的长．
解：（1）证明：，，
，，是等腰三角形.
（2）是边上的中线，，
，，
的周长为33，，即，
解得：．
22. 阅读并完成相应的任务．如图，小明站在堤岸凉亭点处，正对他的点（与堤岸垂直）停有一艘游艇，他想知道凉亭与这艘游艇之间的距离，于是制定了如下方案：
（1）任务一：根据题意将测量方案示意图补充完整；
（2）任务二：
①凉亭与游艇之间距离是_______米；
②请你说明小明方案正确的理由．
解：（1）根据题意将测量方案示意图补充完整如图所示.
（2）①由补充完整的图形可知：，米.
②由题意可得：米，米，，
在和中，，，
米，
小明的方案是正确的．
23. 广场视野开阔，阻挡物少，成为不少市民放风筝的最佳场所，某校七年级（1）班的小明和小亮学习了“勾股定理”之后，为了测得风筝的垂直高度，他们进行了如下操作：①测得水平距离的长为15米；②根据手中剩余线的长度计算出风筝线的长为25米；③牵线放风筝的小明的身高为1.6米．
（1）求风筝的垂直高度；
（2）如果小明想风筝沿方向下降12米，则他应该往回收线多少米？
解：（1）在中，由勾股定理得，
，
所以，（负值舍去），
所以，（米，
答：风筝的高度为21.6米.
（2）由题意得，米，
米，在中，
（米，
（米，
他应该往回收线8米．
24. 某小区在社区管理人员及社区居民的共同努力之下，在临街的拐角建造了一块绿化地（阴影部分）．如图，已知，，，．技术人员通过测量确定了．
（1）小区内部分居民每天必须从点A经过点B再到点C位置，为了方便居民出入，技术人员打算在绿地中开辟一条从点A直通点C的小路，请问如果方案落实施工完成，居民从点A到点C将少走多少路程？
（2）这片绿地的面积是多少？
解：（1）如图，连接，
∵，，，
∴，
∴，
答：居民从点A到点C将少走路程．
（2）∵，．，
∴，
∴是直角三角形，，
∴， ，
∴，
答：这片绿地的面积是．
25. 如图，是边长为6cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿方向匀速移动．
（1）当点P的运动速度是1cm/s，点Q的运动速度是2cm/s，当Q到达点C时，P、Q两点都停止运动，设运动时间为t（s），当时，判断的形状，并说明理由；
（2）当它们的速度都是1cm/s，当点P到达点B时，P、Q两点停止运动，设点P的运动时间为t（s），则当t为何值时，是直角三角形？
解：（1）是等边三角形，理由如下；
由题意得，当时，，
∴，∴，
∵是等边三角形，∴，∴是等边三角形.
（2）∵运动时间为，∴，∴，
如图1所示，当时，
∵，∴，∴，∴，
解得；
如图2所示，当时，
同理可得，∴，∴，
解得；
综上所述，当点P的运动时间为2s或4s时，是直角三角形．
附加题（本题供学有余力的学生尝试解答，不作为考试内容.）
26. 如图，在△ABC中，AB=AC，点D为BC边上一动点（不与点B，C重合），过点D作射线DE交AB于点E，使∠ADE=∠B．
（1）如图1，判断∠BDE与∠CAD的大小关系，并说明理由；
（2）如图2，当∠DAE为直角时，请探索∠ADE与∠CAD的数量关系．
解：（1）∠BDE=∠CAD；理由如下：
因为AB=AC，所以∠B=∠C．
因为∠ADE=∠B，所以∠ADE=∠C．
因为∠BDE+∠ADE+∠ADC=180°，∠CAD+∠C+∠ADC=180°，
所以∠BDE=∠CAD.
（2）因为∠DAE为直角，所以∠B+∠ADB=90°．
即∠B+∠BDE+∠ADE=90°．
由（1）知∠BDE=∠CAD，
又因为∠ADE=∠B，所以2∠ADE+∠CAD=90°．课题
测凉亭与游艇之间的距离
测量工具
皮尺等
测量方案示意图（不完整）

测量步骤
①小明沿堤岸走到电线杆旁（直线与堤岸平行）；
②再往前走相同的距离，到达点；
③他到达点后向左转90度直行，当自己，电线杆与游艇在一条直线上时停下来，此时小明位于点处．
测量数据
米，米，米