2023-2024学年山东省青岛市市北区七年级(上)期中数学试卷（解析版）

这是一份2023-2024学年山东省青岛市市北区七年级(上)期中数学试卷（解析版），共12页。试卷主要包含了选择题，填空题，画图题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8小题，每小题3分，共24分.）
1. 的相反数是（ ）
A. 83B. C. D.
【答案】A
【解析】的相反数是83．
故选：A．
2. 中华民族的母亲河黄河，发源于巴颜喀拉山脉北麓，注入渤海，流域面积约为750000千米2．将750000用科学记数法表示为( )
A. 75×104B. 7.5×104C. 75×105D. 7.5×105
【答案】D
【解析】将750000用科学记数法表示为：7.5×105．
故选：D．
3. 如图，在一密闭的圆柱形玻璃杯中装一半的水，水平放置时，水面的形状是（ ）
A. B.
C. D.
【答案】D
【解析】由水平面与圆柱的底面垂直，得知水面的形状是长方形．
故选：D．
4. 在下列各数中：，，，，，，0．其中是负数的有（ ）个．
A. 2个B. 3个C. 4个D. 5个
【答案】D
【解析】，，，，，
，
∴是负数的有．，，，，共5个.
故选：D．
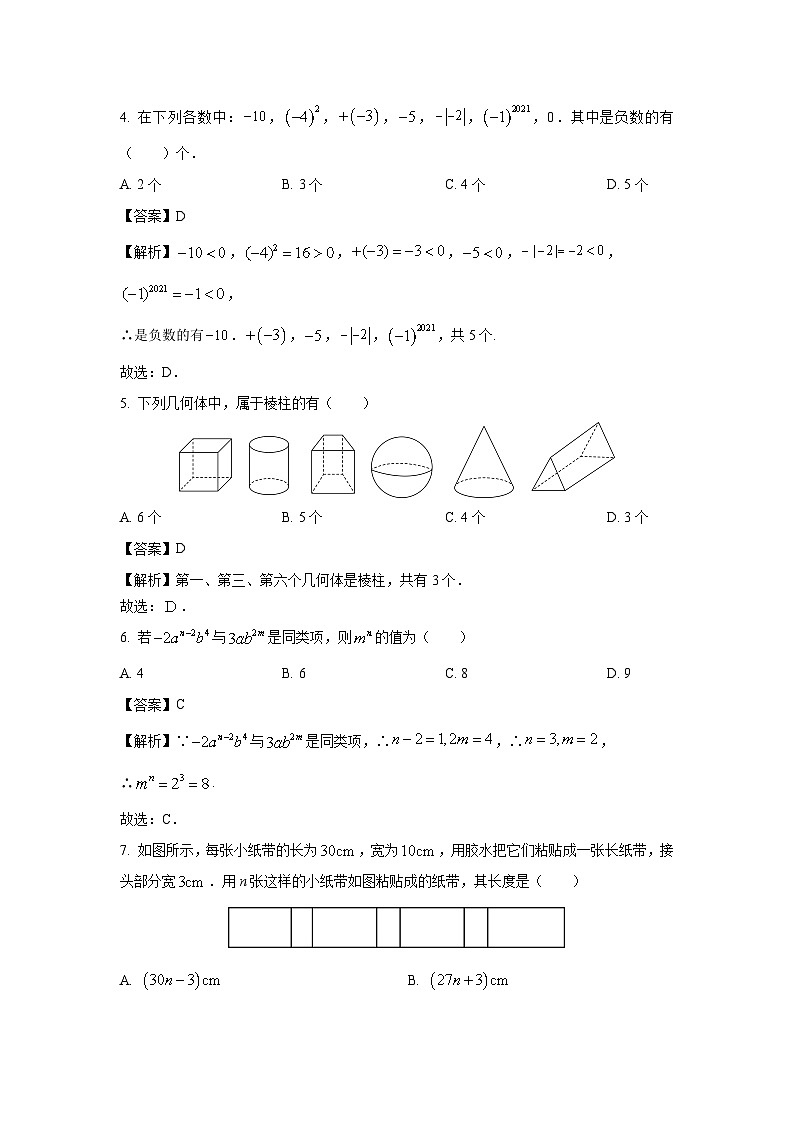
5. 下列几何体中，属于棱柱的有（ ）
A. 6个B. 5个C. 4个D. 3个
【答案】D
【解析】第一、第三、第六个几何体是棱柱，共有3个．
故选：．
6. 若与是同类项，则的值为（ ）
A. 4B. 6C. 8D. 9
【答案】C
【解析】∵与是同类项，∴，∴，
∴.
故选：C．
7. 如图所示，每张小纸带的长为，宽为，用胶水把它们粘贴成一张长纸带，接头部分宽．用n张这样的小纸带如图粘贴成的纸带，其长度是（ ）
A. B.
C. D.
【答案】B
【解析】接头是每相邻两张有一个接头，则三张两个接头，四张三个接头，
推而广之n张有个接头，故n张时总长度为：.
故选：B.
8. 如图是根据幻方改编的“幻圆”游戏，将，2，，0，1，，3，分别填入图中的圆圈内，使横行、竖列以及内外两圈上的4个数字之和都相等．已知图中，，，分别表示一个数，则的值是（ ）
A. B. 1C. 或3D.
【答案】C
【解析】，
所以内外两圈上以及横、竖上的4个数字之和都为，所以，
所以，故或2，
所以或3．
故选：．
二、填空题（本题共6小题，每小题3分，共18分.）
9. 的系数是 ________．
【答案】
【解析】的系数是．
10. 比较大小：_____．
【答案】
【解析】，，，．
11. 铅笔在纸上划过会留下痕迹，这体现的数学知识是点动成线；三角板绕它的一条直角边旋转一周，形成一个圆锥体，这体现的数学知识是______．
【答案】面动成体
【解析】三角板绕它的一条直角边旋转一周，形成一个圆锥体，这说明了面动成体．
12. 某件商品的成本价是元，按成本价提高后标价，又以8折（即按标价的销售，这件商品的售价为 __________元．
【答案】
【解析】依题意得（元．
13. 如图，将刻度尺放在数轴上，若4和6刻度分别与数轴上表示1和2的两点对齐，则数轴上与1刻度对齐的点表示的数为 ___________．
【答案】
【解析】∵4和6刻度分别与数轴上表示1和2的两点对齐，
∴数轴的单位长度是2，∴原点对应2的刻度，
∴数轴上与1刻度对齐的点表示的数是.
14. “24点”是一种益智类游戏，小磊任意抽出4张扑克牌，上面的数字分别是1，2，6，，请用这4个数字进行混合运算（每个数字只能用一次，可以加括号），使其最后结果是24或，列出算式是 ____________________．
【答案】
【解析】．
三、画图题：（本题满分6分.）
15. 如图，是由5个大小相同的小立方体组成的几何体，请分别画出从正面、左面和上面观察该几何体看到的形状图．
解：如图所示，即为所求．
四、解答题（本题满分72分，共有7道小题.）
16. 计算：化简：
（1）；
（2）；
（3）；
（4）．
解：（1）
.
（2）
.
（3）
.
（4）
．
17. 某果品冷库的温度为，现有一批水果要在的温度储藏，如果冷库每小时升高，那么几小时后才能达到所要求的温度？
解：由题意可得，
（小时），
答：5小时后才能达到所要求的温度．
18. 某出租车沿人民路东西方向行驶，如果把人民公园站台记为0，向东行驶记为正，向西行驶记为负，这辆车从人民公园站台出发以后行驶的路程如下表（单位：km）
（1）这辆车离开出发点最远是 千米；
（2）这辆车在上述过程中一共行驶了多少路程？
（3）若汽车耗油量为4升/千米，共耗油多少升？
解：（1）第一次与出发点的距离为，
第二次与出发点的距离为，
第三次与出发点的距离为，
第四次与出发点的距离为|，
第五次与出发点的距离为|，
第六次与出发点的距离为，
第七次与出发点的距离为，
∴这辆车离开出发点最远.
（2），
∴这辆车在上述过程中一共行驶了54km.
（3）∵（升），
∴汽车耗油量为3升/千米，共耗油216升．
19. 如图是一个长方体包装盒展开图，长方体盒子的长是宽的2倍．
（1）盒子展开图的6个面分别标有如图所示的序号，若将展开图重新围成一个包装盒，则①与 相对，②与 相对；（只填序号）
（2）若长方体的宽为，则长方体的长为多少？高为多少？（用含x的代数式表示）
（3）当时，求这种长方体包装盒的体积．
解：（1）根据长方体纸盒展开图可知，①与⑤是相对的，②与④是相对的，③与⑥是相对的.
（2）由长方体的宽为，长是宽的2倍可以得到长方体的长为；
由图可知①与④的高相同，所以长方体的高为．
答：长方体的长为，高为．
（3）当时，长方体的体积为：长宽高．
答：长方体包装盒的体积为．
20. ①．
②．
③．
④．…
（1）根据上述式子所呈现的规律，请写出第n个等式： ；
（2）按（1）中的规律计算：
①；
②．
解：（1）第n个等式：．
（2）①
=
．
②
．
21. 小亮房间窗户的窗帘如图1所示，它是由两个四分之一圆组成（半径相同）．
（1）用代数式表示窗户能射进阳光的部分的面积是 ．（结果保留，窗框面积忽略不计）
（2）当，时，求窗户能射进阳光的部分的面积是多少？
（3）小亮又设计了如图2的窗帘（由一个半圆和两个四分之一圆组成，半径相同），请你帮他算一算：此时窗户能射进阳光的部分的面积是否更大？如果更大，大多少？（结果保留，窗框面积忽略不计）
解：（1）根据圆的面积公式：装饰物的面积是，
∵窗户能射进阳光部分面积是窗户的面积减去装饰物的面积，
∴窗户能射进阳光的面积是.
（2）当，时，.
（3）如图2，窗户能射进阳光的面积，
，，
∴此时，窗户能射进阳光面积更大，
，
∴此时，窗户能射进阳光的面积比原来大．
22. 在解决数学问题时，整体思想有着广泛的应用，尤其在解决整式加减的运算中经常使用．
比如，已知：，求代数式的值．
解：
.
在解决上面问题时，我们无需知道a的具体数值，只需将前两项利用乘法分配律的逆运用，变为已知的形式，再将已知代入求值即可．
请你利用上述整体思想方法，解决以下问题：
（1）若，则 ：
（2）当，求的值．
（3）当时，代数式的值为m，当时，代数式的值是多少？
解：（1）∵，
∴
．
（2）∵，∴，
∴
．
（3）∵当时，代数式的值为m，
∴，
∴，
∴当时，
．
23. 数轴是一种非常重要的数学工具，它使数和数轴上的点建立起对应关系，揭示了数与点之间的内在联系．小亮在草稿纸上画了一条数轴进行操作探究：
操作一：
（1）折叠纸面，使1表示的点与表示的点重合，则表示的点与__表示的点重合；
操作二：
（2）折叠纸面，使1表示的点与表示的点重合，则3表示的点与__表示的点重合；假如A、B两点经过折叠后重合，且数轴上A、B两点之间距离为5（A在B的左侧），则A、B两点表示的数分别是A：__，B：__；
操作三：
（3）在数轴上剪下从到2，长度是8个单位的一条线段，并把这条线段沿某点折叠，然后在重叠部分某处剪一刀（如图），展开后得到三条线段．若这三条线段的长度之比为1：1：2，则折痕处对应的点所表示的数可能是 __．
解：（1）∵1表示的点与表示的点重合，
∴由对称性找到折痕的点为原点O，则与2重合．
（2）∵1表示的点与表示的点重合，
∴根据对称性找到折痕的点为，
设3表示的点与数a表示的点重合，
∴，解得：，
∵，∴A到折痕的点距离为，
∵A在B的左侧，∴A表示的数：，
B表示的数：．
（3）如图：①当时，
设，
∵，∴，解得：，
∴，
∴折痕处所表示的数为：；
②当时，
设，
∵，∴，解得：，
∴；
∴折痕处所表示的数为：；
③当时，
设，
∵，∴，解得：，
∴；
∴折痕处所表示的数为：；
综上所述：折痕处所表示的数可能为：1或2或3．序号
1
2
3
4
5
6
7
路程