浙教版（2024）七年级上册（2024）5.5 一元一次方程的应用优质ppt课件

这是一份浙教版（2024）七年级上册（2024）5.5 一元一次方程的应用优质ppt课件，文件包含553一元一次方程的应用pptx、教案553一元一次方程的应用docx、学案553一元一次方程的应用docx等3份课件配套教学资源，其中PPT共42页， 欢迎下载使用。

1. 学生能够熟练运用一元一次方程解决调配问题，理解调配中数量关系的变化；2. 掌握行程问题中速度、时间、路程的关系，能用方程准确求解相关问题；3. 培养学生分析实际问题、建立方程模型的能力，提高逻辑思维和解决问题的能力。
一项任务，甲车间单独做需要12天完成，乙车间单独做需要15天完成。两车间合作4天后，由乙车间单独完成。思考：乙车间单独做了几天？
某家具厂生产一种方桌，1立方米的木材可做50个桌面或300条桌腿，现有10立方米的木材，怎样分配生产桌面和桌腿使用的木材，才能使桌面、桌腿刚好配套，共可生产多少张方桌?(一张方桌有1个桌面，4条桌腿)思考：调配问题应如何作解？
劳力调配问题的关键：劳力调配问题要搞清人数的变化，常见题型有(1)既有调入又有调出；(2)只有调入没有调出，调入部分变化，其余不变；(3)只有调出没有调入，调出部分变化，其余不变。
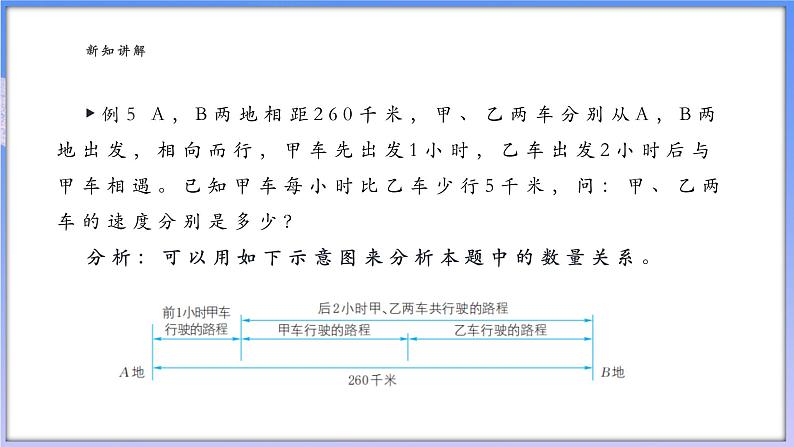
▶例5 A，B两地相距260千米，甲、乙两车分别从A，B两地出发，相向而行，甲车先出发1小时，乙车出发2小时后与甲车相遇。已知甲车每小时比乙车少行5千米，问：甲、乙两车的速度分别是多少？分析：可以用如下示意图来分析本题中的数量关系。
根据这一相等关系，设乙车的速度为xkm/h，可列出方程。解：设乙车的速度为xkm/h，则甲车的速度为(x－5)km/h，由题意，得(x－5)＋2(x＋x－5)＝260。解这个方程，得x＝55。所以甲车的速度为55－5＝50（km/h）。答：甲车的速度为50km/h，乙车的速度为55km/h。
行程问题的关键：行程问题是反映物体匀速运动的应用题，涉及的变化较多，一个、两个或多个物体的运动，可分为“相向运动”（相遇问题）、“同向运动”（追及问题）和“相背运动”（相离问题）三种情况。可以归纳为：速度×时间=路程。
行程问题：相等关系:路程=速度×时间；速度=路程÷时间；时间=路程÷速度；(1)直线形相遇问题:甲走的路程+乙走的路程=两地之间的距离；(2)直线形追及问题:快者走的路程=慢者走的路程+两人初始距离差;快者所走的路程=慢者先走的路程+慢者后走的路程。
其他行程问题中的相等关系。(1)航行问题:顺水速度=静水速度水速;逆水速度=静水速度-水速。(2)火车过桥问题:①从车头刚上桥到车尾离开桥:过桥速度×过桥时间:桥长+车长;②火车过桥全路程-桥长=车长。
▶例6 学校组织植树活动，已知在甲地植树的有23人，在乙地植树的有17人。现调20人去支援，使在甲地植树的人数是乙地植树人数的2倍，问：应调往甲、乙两地各多少人？
分析：设应调往甲地x人，题中所涉及的有关数量及其关系可以用下表表示：
解：设应调往甲地x人，根据题意，得23＋x＝2（17＋20－x）。解这个方程，得x＝17。所以调往乙地的人数为20－x＝20－17＝3。答：应调往甲地17人，乙地3人
如 果 设 调 往 乙地的人数为 x，方程应怎么列？
【例1】某校组织七年级(1)班学生分成甲、乙两队参加社会劳动实践,其中甲队人数是乙队人数的2倍,后因劳动需要,从甲队抽调16人支援乙队,这时甲队人数是乙队人数的一半,则甲队原来有_______人。
【例2】某年亚运会组委会组织高校学生去做志愿者,已知去乒乓球赛场的有10人,去羽毛球赛场的有16人,现调10人去支援,使在羽毛球赛场的人数是在乒乓球赛场人数的2倍,设应调往乒乓球赛场x人,则可列方程为（ ）A.10+x=2(16+10-x)B.2(10+x)=16+10-xC.10+10-x=2(16+x)D.2(10+10-x)=16+x
B 【解析】因为调往乒乓球赛场x人,所以调段,逐一分析往羽毛球赛场(10-x)人.根据题意得2(10+x)=16+10-x.故选B.
【例4】一队学生去校外参加劳动,以4km/h的速度步行前往,走了半小时,学校有紧急通知要传给队长,通讯员以14km/h的速度按原路追上去,则通讯员追上学生队伍所需的时间是（ ）A.10min B.11min C.12min D.13min
【选做】6.劳动课上杨老师带领七(1)班50名学生制作圆柱形小鼓,其中男生人数比女生人数少6人,并且每名学生每小时可制作2个鼓身或剪6个鼓面。(1)男生有_______人，女生有_______人。(2)①老师组织全班学生制作小鼓,要求一个鼓身配两个鼓面,为了使每小时制作的鼓身与剪出的鼓面刚好配套,应该分配多少名学生制作鼓身?多少名学生剪鼓面?②若想每小时制作90个小鼓,且制作的鼓身与剪出的鼓面刚好配套,应再加入多少名学生?
【解析】(1)设男生有x人,则女生有(50-x)人由题意x+6=50-x,解得x=22,所以50-x=28,即男生有22人,女生有28人,故答案为22,28。(2)①设分配y名学生制作鼓身,则(50-y)名学生剪鼓面.由题意,得2×2y=6(50-y),解得y=30,则50-y=20.答:应分配30名学生制作鼓身,20名学生剪鼓面。②由①知分配30名学生制作鼓身,20名学生剪鼓面,则1小时可制作小鼓30×2=60(个)，还需制作90-60=30(个)小鼓,所以应再加人(30÷2)+(30×2÷6)=25(名)学生。
知识点1 劳力调配问题：劳力调配问题要搞清人数的变化，常见题型有(1)既有调入又有调出；(2)只有调入没有调出，调入部分变化，其余不变；(3)只有调出没有调入，调出部分变化，其余不变。
知识点2 行程问题：相等关系:路程=速度×时间；速度=路程÷时间；时间=路程÷速度；(1)直线形相遇问题:甲走的路程+乙走的路程=两地之间的距离；(2)直线形追及问题:快者走的路程=慢者走的路程+两人初始距离差;快者所走的路程=慢者先走的路程+慢者后走的路程。
【必做】1.某车间为提高生产总量在原有16名工人的基础上,新调入若干名工人,使得调整后车间的总人数比调入工人人数的3倍多4人。(1)求调人多少名工人;(2)每名工人每天可以生产1200个螺桂或2000个螺母,1个螺柱需要2个螺母,为使天生产的螺柱和螺母刚好配套,应该安排生产螺柱和螺母的工人各多少名?
【解析】(1)设调入x名工人.根据题意得16+x=3x+4,解得x=6,故调入6名工人.(2)16+6=22(名).设y名工人生产螺柱,则(22-y)名工人生产螺母.根据题意得2×1200y=2000(22-y),解得y=10,则22-y=22-10=12，所以10名工人生产螺柱,12名工人生产螺母。
【必做】2.某桥长1200m,现有一列匀速行驶的火车从桥上通过,测得火车从上桥到完全过桥共用50s,而整个火车在桥上的时间是30s,则火车的速度为_______。
30 m/s【解析】火车“完全通过”和“完全在桥上”是两种不同的情况、可以借助如图所示线段图理解.(1)火车完全通过:(2)火车完全在桥上:
【必做】3.一艘轮船从河的上游甲港顺流到达下游的丙港,然后调头逆流向上到达中游的乙港,共用了12小时.已知这艘轮船的顺流速度是逆流速度的2倍,水流速度是每小时2千米,从甲港到乙港相距18千米,则甲丙两港间的距离为_______千米。
【必做】4.正方形ABCD的轨道上有两个点甲与乙,开始时甲在A处,乙在C处,它们沿着正方形轨道按顺时针方向同时出发,甲的速度为每秒1cm,乙的速度为每秒5cm,已知正方形轨道ABCD的边长为2cm,则乙在第2023次追上甲时的位置在（ ）A.AB上 B.BC上 C.CD上 D.AD上
C【解析】设乙走x秒第1次追上甲,根据题意,得5x-x=4,解得x=1,所以乙走1秒第1次追上甲,则乙在第1次追上甲时的位置在AB上,设乙再走y秒第2次追上甲.根据题意,得5y-y=8,解得y=2,所以乙再走2秒第2次追上甲,则乙在第二次追上甲时的位置在BC上.易得乙再走2秒第3次追上甲,则乙在第3次追上甲时的位置在CD上.乙再走2秒第4次追上甲,则乙在第4次追上甲时的位置在DA上.乙再走2秒第5次追上甲,则乙在第5次追上甲时的位置又回到AB上.故每4次为一个循环.因为2023÷4=505……3,所以乙在第2023次追上甲时的位置与第3次追上甲时的位置相同,在CD上.故选C.
【选做】5.某人乘船由A地顺流而下到B地,然后又逆流而上到C地,共乘船6h,已知船在静水中的速度是16km/h,水流速度是4km/h,若A,C两地的距离为4km,则A,B两地间的距离是_______km.
【选做】6.上午8点零8分，小明骑自行车从家里出发，8分钟后，爸爸骑摩托车去追他，在离家4千米的地方追上了他。然后爸爸立刻回家，到家后又立刻回头去追小明，再追上他的时候，离家恰好是8千米，问这时是几点几分？
8点32分【解析】设第一次t分追上，小明速度为v(千米/时)。从第一次追上到第二次追上时,小明走4千米,爸爸走 12千米,则爸爸的速度是3v。3v·t=(8+t)·v , 3t=8+t , t=4 小明行4千米,用4+8=12(分), 行8千米用24分，所以这时是8点32分。
【拓展题】某条城际铁路线共A.B,C三个车站,每日上午均有两班次列车加A站驶往C站,其中D1001次列车从A站发,经停B站后到达C站,G1002次列车从A站始发,直达C站,两个车次的列车在行驶过程中保持各自的行驶速度不变,某校数学学习小绍对列车运行情况进行研究,收集到列车运行信息如下表所示。