初中数学数学活动习题课件ppt

这是一份初中数学数学活动习题课件ppt，共23页。PPT课件主要包含了x＋33，即结果都为0，＋x＋8＝5x，值理由如下，＝x－8，为－14，x＋y，答案不唯一，理由如下等内容，欢迎下载使用。
题型一　与月历有关的问题
1. 在如图的某月份的月历表中，任意框出表中竖列 上三个相邻的数，这三个数的和不可能是（　A　）
2. 如图是某年某月的月历表，若用一个方框刚好框 住月历上的4个数： ，请找出这4个数之间的关 系后回答：框住4个数的和不可能为下列哪个数？ （　B　）
3. 2024年3月共有五个星期六，已知第一个星期六 是3月2日，那么第五个星期六是3月 日.4. 如图是2024年1月的月历表：
（1）在图中用优美的“ ”U形框框住五个数， 其中最小的数为1，则U形框中的五个数字之和 为 ⁠；
（2）在图中将U形框上下左右移动，框住月历表中 的5个数字，设最小的数字为x，用含x的式子表示 U形框框住的五个数字之和为 ⁠.
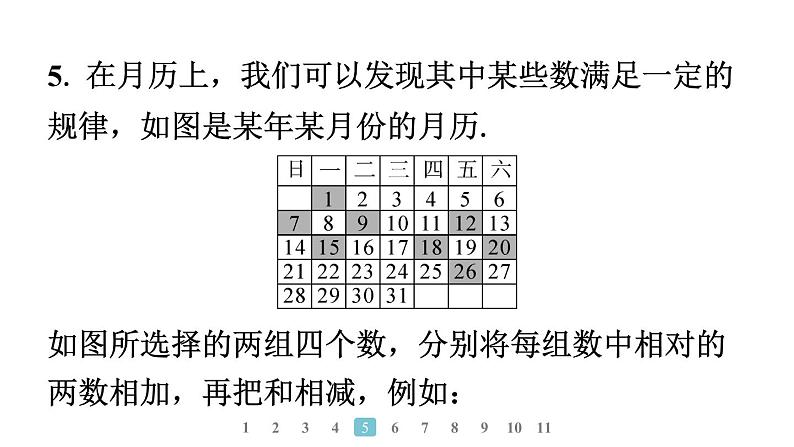
5. 在月历上，我们可以发现其中某些数满足一定的 规律，如图是某年某月份的月历.
如图所选择的两组四个数，分别将每组数中相对的 两数相加，再把和相减，例如：
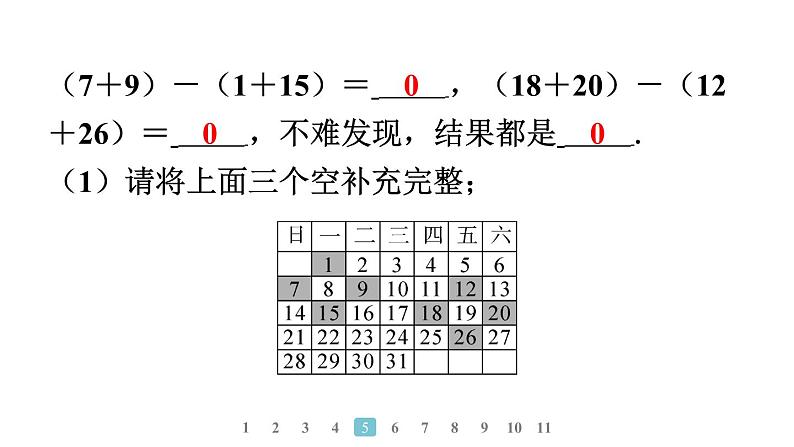
（7＋9）－（1＋15）＝ ，（18＋20）－（12 ＋26）＝ ，不难发现，结果都是 ⁠.（1）请将上面三个空补充完整；
（2）我们发现选择其他类似的部分规律也相同，请 你利用整式的运算对以上的规律加以证明.解：设正中间的数为a，则周围的四个数分别为a－7，a＋7，a－1，a＋1.所以[（a－1）＋（a＋1）]－[（a－7）＋（a＋ 7）]＝2a－2a＝0，即结果都为0.
解：设正中间的数为a，
则周围的四个数分别为a－7，a＋7，a－1，a＋1.
所以[（a－1）＋（a＋1）]－[（a－7）＋（a＋
7）]＝2a－2a＝0，
6. （2023－2024·南阳唐河县期末）如图①是某年11 月的月历，用如图②的“Z”字形覆盖住月历中的 五个数，这五个数从小到大依次为A，B，C， D，E. 这五个数的和能被5整除吗？为什么？
（1）甲同学设A＝x，通过计算得出了结论，乙同 学说自己设C＝x更简单，请你分别写出甲、乙同 学的解题思路.
解：（1）甲同学方法：设A＝x，则B＝x＋1，C ＝x＋8，D＝x＋15，E＝x＋16，所以A＋B＋C＋D＋E＝x＋x＋1＋x＋8＋x＋ 15＋x＋16＝5x＋40＝5（x＋8），因为5（x＋8）能被5整除，所以这五个数的和能被5整除.乙同学方法：设C＝x，则D＝x＋7，E＝x＋8， B＝x－7，A＝x－8，
解：（1）甲同学方法：设A＝x，则B＝x＋1，C
＝x＋8，D＝x＋15，E＝x＋16，
所以A＋B＋C＋D＋E＝x＋x＋1＋x＋8＋x＋
15＋x＋16＝5x＋40＝5（x＋8），
因为5（x＋8）能被5整除，
所以这五个数的和能被5整除.
乙同学方法：设C＝x，则D＝x＋7，E＝x＋8，
B＝x－7，A＝x－8，
所以A＋B＋C＋D＋E＝x－8＋x－7＋x＋x＋7 ＋x＋8＝5x.因为5x能被5整除，所以这五个数的和能被5整除.
所以A＋B＋C＋D＋E＝x－8＋x－7＋x＋x＋7
因为5x能被5整除，所以这五个数的和能被5整除.
（2）小明受到启发，改编了一道题目，请你来解 答：代数式A－2B＋3C＋4D－6E的值是否为定 值？若是，请求出它的值；若不是，请说明理由.
解：（2）代数式A－2B＋3C＋4D－6E的值是定 值，理由如下：设C＝x，则D＝x＋7，E＝x＋8，B＝x－7，A ＝x－8，所以A－2B＋3C＋4D－6E＝x－8－2（x－7） ＋3x＋4（x＋7）－6（x＋8）＝－14.所以代数式A－2B＋3C＋4D－6E的值是定值， 为－14.
解：（2）代数式A－2B＋3C＋4D－6E的值是定
设C＝x，则D＝x＋7，E＝x＋8，B＝x－7，A
所以A－2B＋3C＋4D－6E＝x－8－2（x－7）
＋3x＋4（x＋7）－6（x＋8）＝－14.
所以代数式A－2B＋3C＋4D－6E的值是定值，
题型二　代数推理相关问题7. 有五个连续自然数，若第三个数为a，则这五个 数的和是 ⁠.8. 设x表示三位数，y表示两位数，如果把x放在y 的左边组成一个五位数，那么这个五位数可表示 为 ⁠.
9. 对任意一个四位数n，如果千位与十位上的数字 之和为9，百位与个位上的数字之和也为9，那么称 n为“极数”.（1）请任意写出两个“极 数”： ， ；（答案不唯一）（2）猜想任意一个“极数”是否是99的倍数，请说 明理由.
解：任意一个“极数”都是99的倍数，理由如下：设这个“极数”的千位数字为a，百位数字为b，则这个数表示为1000a＋100b＋10（9－a）＋（9 －b）＝1000a＋100b＋90－10a＋9－b＝990a＋ 99b＋99＝99（10a＋b＋1），因为10a＋b＋1为正整数，所以任意一个“极数”都是99的倍数.
解：任意一个“极数”都是99的倍数，理由如下：
设这个“极数”的千位数字为a，百位数字为b，
则这个数表示为1000a＋100b＋10（9－a）＋（9
－b）＝1000a＋100b＋90－10a＋9－b＝990a＋
99b＋99＝99（10a＋b＋1），
因为10a＋b＋1为正整数，
所以任意一个“极数”都是99的倍数.
10. 教材P106素材题一个三位数的百位数字是a， 十位数字是b，个位数字是c（a≠0，c≠0）.（1）列式表示这个三位数.解：（1）这个三位数为100a＋10b＋c.（2）将该数的个位数字移到原来百位数字的左边， 得到一个新的三位数.①列式表示这个新三位数.②计算新三位数与原三位数之差的绝对值，该绝对 值能被9整除吗？说明理由.
解：（1）这个三位数为100a＋10b＋c.
解：（2）①由题意得这个新的三位数，其百位数字 是c，十位数字是a，个位数字是b，所以这个新三位数为100c＋10a＋b.②新三位数与原三位数之差的绝对值能被9整除.理由如下：因为｜（100c＋10a＋b）－（100a＋10b＋c）｜ ＝｜99c－90a－9b｜＝9｜11c－10a－b｜.所以新三位数与原三位数之差的绝对值能被9整除.
解：（2）①由题意得这个新的三位数，其百位数字
是c，十位数字是a，个位数字是b，
所以这个新三位数为100c＋10a＋b.
②新三位数与原三位数之差的绝对值能被9整除.
因为｜（100c＋10a＋b）－（100a＋10b＋c）｜
＝｜99c－90a－9b｜＝9｜11c－10a－b｜.
所以新三位数与原三位数之差的绝对值能被9整除.
11. （2024·厦门同安区期末）观察下列三组整式 组，回答下列问题：第一组：2x，－2y；第二组：4m－n，－3n；第三组：4s＋t，2s－2t，－3s－2t.（1）将上述每组整式分别相加后，发现所有单项式 的系数和为 ⁠；
（2）若满足此特征的整式组称为“O系整式组”， 则2m－3n，－5m＋9n，－3m－n这一组整式 组 （填“能”或“不能”）构成“O系整 式组”；