上海市建平实验中学2024-2025学年七年级上学期期中考试数学试卷

这是一份上海市建平实验中学2024-2025学年七年级上学期期中考试数学试卷，共14页。试卷主要包含了选择题，填空题，简答题，解答题等内容，欢迎下载使用。
1．（3分）下列各式中，整式的个数有（ ）
①x+6；②3﹣2x＝1；③；④0；⑤；⑥
A．3个B．4个C．5个D．6个
2．（3分）计算（﹣）2021•（﹣）2022的结果是（ ）
A．B．
C．D．
3．（3分）下列各式从左到右的变形，是因式分解的是（ ）
A．（a+b）（a﹣b）＝a2﹣b2
B．a2﹣b2＝（a+b）（a﹣b）+1
C．a2﹣a﹣1＝a（a﹣1）﹣1
D．a3+2a2+3a＝a（a2+2a+3）
4．（3分）下列整式的乘法中，不能用平方差公式进行计算的是（ ）
A．（x+y）（x﹣y）B．（﹣x﹣y）（﹣x+y）
C．（﹣x﹣y）（x+y）D．（﹣x+y）（x+y）
5．（3分）如果多项式A、B的次数都是八次，那么A﹣B的次数（ ）
A．低于八次B．等于八次
C．不低于八次D．不高于八次
6．（3分）如图，正方形卡片A类、B类和长方形卡片C类各若干张，如果要拼一个长为（a+3b），宽为（2a+b）的大长方形，则需要A类、B类和C类卡片的张数分别为（ ）
A．2，5，3B．3，7，2C．2，3，7D．2，5，7
二、填空题：（本大题共12题，每题2分，满分24分）
7．（2分）练习本每本a元，铅笔每支b元，买3本练习本和10支笔，共付 元．
8．（2分）多项式2y3﹣9y2+7xy+1是 次 项式．
9．（2分）把整式按照字母x降幂排列为 ．
10．（2分）已知单项式3xm+1y4与是同类项，则m+n＝ ．
11．（2分）计算：（﹣3a2b）3＝ ．
12．（2分）已知整式（x+3）（x﹣a）中无一次项，求a＝ ．
13．（2分）计算：＝ ．
14．（2分）若2x+5y﹣3＝0，则4x•32y的值为 ．
15．（2分）因式分解：15a2b﹣3ab＝ ．
16．（2分）因式分解：ax﹣ay+2x﹣2y＝ ．
17．（2分）如果4x2+（m﹣1）x+25是一个完全平方式，那么常数m＝ ．
18．（2分）我们学习了幂的意义，知道an表示n个a相乘，并且由an＝m，知道a和n可以求m．我们不妨思考，如果知道a，m，能否求n呢？对于an＝m，规定[a，m]＝n，例如：62＝36，所以[6，36]＝2．如果[3，x]＝m，[3，y]＝m+2，那么y＝ ．（用含x的代数式表示y）
三、简答题：（本大题共6题，每题5分，满分30分）
19．（5分）计算：（﹣2a3）2+（﹣a2）3﹣a•a2•a3．
20．（5分）计算：﹣8x2﹣[6﹣2x（x﹣3y）]+6（x+1）（x+y）．
21．（5分）计算：（3a﹣2）2﹣（3a+2）（﹣3a+2）．
22．（5分）计算：（2x+y﹣3）（2x﹣y+3）．
23．（5分）运用整式乘法公式进行计算：20242﹣2023×2025．
24．（5分）因式分解：2x2（a+b）2﹣2xy（a+b）2﹣12y2（﹣a﹣b）2．
四、解答题（本大题共4题，25题7分，26，27题每题8分，28题5分，满分28分）
25．（7分）先化简，再求值：（9an+2+6a3n﹣1﹣an）÷（﹣6an﹣1）+（﹣an+1）2÷（﹣a）2（n为正整数），其中a＝﹣2．
26．（8分）已知A＝b2﹣a2+5ab，B＝3ab+2b2﹣a2．
（1）化简：3A﹣B；
（2）已知a、b满足（a+1）2+|b+2|＝0，求3A﹣B的值．
27．（8分）图1是一个长方形窗户ABCD，它是由上下两个长方形（长方形AEFD和长方形EBCF）的小窗户组成，在这两个小窗户上各安装了一个可以朝一个方向水平方向拉伸的遮阳帘，这两个遮阳帘的高度分别是a和2b（即DF＝a，BE＝2b），且b＞a＞0．当遮阳帘没有拉伸时（如图1），窗户的透光面积就是整个长方形窗户（长方形ABCD）的面积．
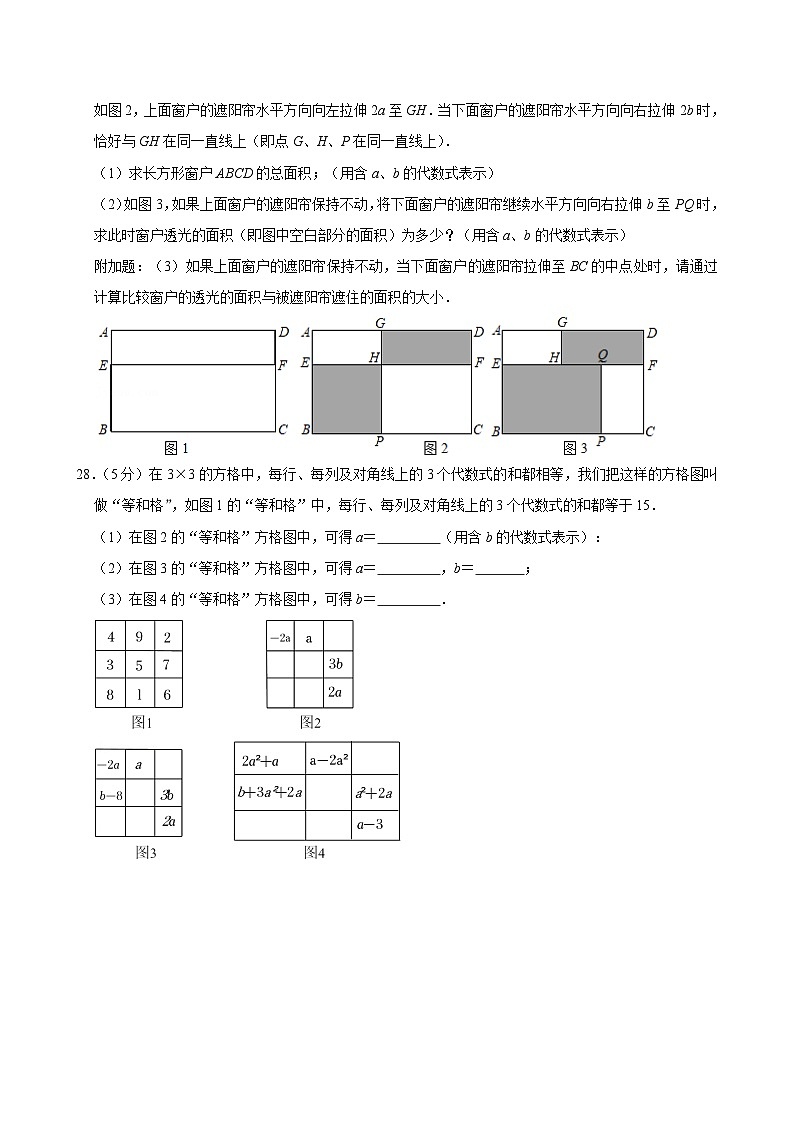
如图2，上面窗户的遮阳帘水平方向向左拉伸2a至GH．当下面窗户的遮阳帘水平方向向右拉伸2b时，恰好与GH在同一直线上（即点G、H、P在同一直线上）．
（1）求长方形窗户ABCD的总面积；（用含a、b的代数式表示）
（2）如图3，如果上面窗户的遮阳帘保持不动，将下面窗户的遮阳帘继续水平方向向右拉伸b至PQ时，求此时窗户透光的面积（即图中空白部分的面积）为多少？（用含a、b的代数式表示）
附加题：（3）如果上面窗户的遮阳帘保持不动，当下面窗户的遮阳帘拉伸至BC的中点处时，请通过计算比较窗户的透光的面积与被遮阳帘遮住的面积的大小．
28．（5分）在3×3的方格中，每行、每列及对角线上的3个代数式的和都相等，我们把这样的方格图叫做“等和格”，如图1的“等和格”中，每行、每列及对角线上的3个代数式的和都等于15．
（1）在图2的“等和格”方格图中，可得a＝ （用含b的代数式表示）：
（2）在图3的“等和格”方格图中，可得a＝ ，b＝ ；
（3）在图4的“等和格”方格图中，可得b＝ ．
2024-2025学年上海市浦东新区建平实验中学七年级（上）期中数学试卷
参考答案与试题解析
一、选择题：（本大题共6题，每题3分，满分18分）
1．（3分）下列各式中，整式的个数有（ ）
①x+6；②3﹣2x＝1；③；④0；⑤；⑥
A．3个B．4个C．5个D．6个
【答案】B
【分析】直接利用单项式和多项式统称为整式，进而分析得出答案．
【解答】解：整式有：①x+6；③；④0；⑥﹣，共有4个．
故选：B．
2．（3分）计算（﹣）2021•（﹣）2022的结果是（ ）
A．B．
C．D．
【答案】B
【分析】根据幂的乘方运算以及积的乘方运算即可求出答案．
【解答】解：原式＝[（﹣）×（﹣）]2021×（﹣）
＝12021×（﹣）
＝﹣，
故选：B．
3．（3分）下列各式从左到右的变形，是因式分解的是（ ）
A．（a+b）（a﹣b）＝a2﹣b2
B．a2﹣b2＝（a+b）（a﹣b）+1
C．a2﹣a﹣1＝a（a﹣1）﹣1
D．a3+2a2+3a＝a（a2+2a+3）
【答案】D
【分析】根据因式分解的定义对各选项进行逐一分析即可．
【解答】解：A、（a+b）（a﹣b）＝a2﹣b2，从左到右是整式的乘法，不是因式分解；
B、a2﹣b2＝（a+b）（a﹣b）+1，等式的右边不是几个整式的积，不是因式分解；
C、a2﹣a﹣1＝a（a﹣1）﹣1，等式的右边不是几个整式的积，不是因式分解；
D、a3+2a2+3a＝a（a2+2a+3），等式的右边是几个因式积的形式，故是因式分解；
故选：D．
4．（3分）下列整式的乘法中，不能用平方差公式进行计算的是（ ）
A．（x+y）（x﹣y）B．（﹣x﹣y）（﹣x+y）
C．（﹣x﹣y）（x+y）D．（﹣x+y）（x+y）
【答案】C
【分析】利用平方差公式的结构特征判断即可．
【解答】解：A、原式＝x2﹣y2，不符合题意；
B、原式＝（﹣x）2﹣y2＝x2﹣y2，不符合题意；
C、原式＝﹣（x+y）2＝﹣x2﹣2xy﹣y2，符合题意；
D、原式＝y2﹣x2，不符合题意．
故选：C．
5．（3分）如果多项式A、B的次数都是八次，那么A﹣B的次数（ ）
A．低于八次B．等于八次
C．不低于八次D．不高于八次
【答案】D
【分析】根据多项式减多项式的方法可知，两式作差后的最后次数不高于原来两个多项式的最高次数．
【解答】解：∵多项式A、B的次数都是八次，
∴A﹣B的次数不高于八次，
故选：D．
6．（3分）如图，正方形卡片A类、B类和长方形卡片C类各若干张，如果要拼一个长为（a+3b），宽为（2a+b）的大长方形，则需要A类、B类和C类卡片的张数分别为（ ）
A．2，5，3B．3，7，2C．2，3，7D．2，5，7
【答案】C
【分析】根据多项式乘多项式的运算法则可求出长方形的面积．
【解答】解：长方形的面积为（a+3b）（2a+b）＝2a2+7ab+3b2，
∵A类卡片的面积为a2，B类卡片的面积为b2，C类卡片的面积为ab，
∴需要A类卡片2张，B类卡片3张，C类卡片7张．
故选：C．
二、填空题：（本大题共12题，每题2分，满分24分）
7．（2分）练习本每本a元，铅笔每支b元，买3本练习本和10支笔，共付 （3a+10b） 元．
【答案】（3a+10b）．
【分析】根据练习本每本a元，铅笔每支b元，可以用含a、b的代数式表示出买3本练习本和10支笔共付的钱数．
【解答】解：∵练习本每本a元，铅笔每支b元，
∴买3本练习本和10支笔，共付（3a+10b）元，
故答案为：（3a+10b）．
8．（2分）多项式2y3﹣9y2+7xy+1是 三 次 四 项式．
【答案】三，四．
【分析】根据多项式的性质进行解答．多项式的次数是多项式中最高次项的次数，多项式的项数为组成多项式的单项式的个数．
【解答】解：多项式2y3﹣9y2+7xy+1中最高次项是2y3，次数是3，由四个单项式组成．
故答案为：三，四．
9．（2分）把整式按照字母x降幂排列为 ．
【答案】．
【分析】先分清各项，再根据多项式幂的排列的定义解答．
【解答】解：按照字母x降幂排列：．
故答案为：．
10．（2分）已知单项式3xm+1y4与是同类项，则m+n＝ 8 ．
【答案】8．
【分析】根据同类项的定义（所含字母相同，相同字母的指数相同）列出方程，求出n，m的值，再代入代数式计算即可．
【解答】解：由题意得，m+1＝3，n﹣2＝4，
解得m＝2，n＝6，
所以m+n＝8．
故答案为：8．
11．（2分）计算：（﹣3a2b）3＝ ﹣27a6b3 ．
【答案】见试题解答内容
【分析】根据积的乘方与幂的乘方运算法则进行计算．
【解答】解：原式＝（﹣3）3•（a2）3•b3
＝﹣27a6b3，
故答案为：﹣27a6b3．
12．（2分）已知整式（x+3）（x﹣a）中无一次项，求a＝ 3 ．
【答案】3．
【分析】先根据多项式乘多项式法则计算，再根据结果中无一次项得出3﹣a＝0，即可求出a的值．
【解答】解：（x+3）（x﹣a）
＝x2﹣ax+3x﹣3a
＝x2+（3﹣a）x﹣3a，
∵整式（x+3）（x﹣a）中无一次项，
∴3﹣a＝0，
∴a＝3，
故答案为：3．
13．（2分）计算：＝ ．
【答案】．
【分析】根据多项式除以单项式的运算法则计算即可．
【解答】解：
＝
＝．
14．（2分）若2x+5y﹣3＝0，则4x•32y的值为 8 ．
【答案】见试题解答内容
【分析】根据同底数的乘法和幂的乘方的性质，先都化成以2为底数的幂相乘的形式，再代入已知条件计算即可．
【解答】解：∵2x+5y﹣3＝0，
∴2x+5y＝3，
∴4x•32y＝22x•25y＝22x+5y＝23＝8．
故答案为：8．
15．（2分）因式分解：15a2b﹣3ab＝ 3ab（5a﹣1） ．
【答案】见试题解答内容
【分析】先确定公因式为3ab，然后提取公因式后整理即可．
【解答】解：15a2b﹣3ab＝3ab（5a﹣1）．
故答案为：3ab（5a﹣1）．
16．（2分）因式分解：ax﹣ay+2x﹣2y＝ （x﹣y）（a+2） ．
【答案】（x﹣y）（a+2）．
【分析】根据题意，先把ax﹣ay+2x﹣2y，分组得（ax﹣ay）+（2x﹣2y），然后再提取公因式，得出a（x﹣y）+2（x﹣y），最后再提取公因式即可得出答案．
【解答】解：ax﹣ay+2x﹣2y
＝（ax﹣ay）+（2x﹣2y）
＝a（x﹣y）+2（x﹣y）
＝（x﹣y）（a+2）．
故答案为：（x﹣y）（a+2）．
17．（2分）如果4x2+（m﹣1）x+25是一个完全平方式，那么常数m＝ 21或﹣19 ．
【答案】21或﹣19．
【分析】利用完全平方公式的结构特征判断，即可得出m的值．
【解答】解：∵4x2+（m﹣1）x+25是一个完全平方式，
∴（m﹣1）x＝±2×2x×5，即（m﹣1）x＝±20x，
∴m﹣1＝±20，
解得：m＝21或﹣19．
故答案为：21或﹣19．
18．（2分）我们学习了幂的意义，知道an表示n个a相乘，并且由an＝m，知道a和n可以求m．我们不妨思考，如果知道a，m，能否求n呢？对于an＝m，规定[a，m]＝n，例如：62＝36，所以[6，36]＝2．如果[3，x]＝m，[3，y]＝m+2，那么y＝ 9x ．（用含x的代数式表示y）
【答案】9x．
【分析】根据新定义运算法则得到：3m＝x，3m+2＝y，据此解答．
【解答】解：根据题意知：3m＝x，3m+2＝y．
所以y＝3m×32＝9x，即y＝9x．
故答案为：9x．
三、简答题：（本大题共6题，每题5分，满分30分）
19．（5分）计算：（﹣2a3）2+（﹣a2）3﹣a•a2•a3．
【答案】2a6．
【分析】先根据积的乘方、幂的乘方法则计算乘方，再根据同底数幂相乘法则计算乘法，最后利用合并同类项法则计算加减即可．
【解答】解：原式＝4a6+（﹣a6）﹣a6
＝4a6﹣a6﹣a6
＝2a6．
20．（5分）计算：﹣8x2﹣[6﹣2x（x﹣3y）]+6（x+1）（x+y）．
【答案】6x+6y﹣6．
【分析】根据整式的混合运算法则，利用单项式乘多项式的运算法则，多项式乘多项式的运算法则进行计算，最后合并同类项即可．
【解答】解：﹣8x2﹣[6﹣2x（x﹣3y）]+6（x+1）（x+y）
＝﹣8x2﹣（6﹣2x2+6xy）+6（x2+xy+x+y）
＝﹣8x2﹣6+2x2﹣6xy+6x2+6xy+6x+6y
＝6x+6y﹣6．
21．（5分）计算：（3a﹣2）2﹣（3a+2）（﹣3a+2）．
【答案】18a2﹣12a．
【分析】先根据平方差公式、完全平方公式计算，再合并同类项即可．
【解答】解：（3a﹣2）2﹣（3a+2）（﹣3a+2）
＝（3a﹣2）2﹣（2+3a）（2﹣3a）
＝9a2﹣12a+4﹣（4﹣9a2）
＝9a2﹣12a+4﹣4+9a2
＝18a2﹣12a．
22．（5分）计算：（2x+y﹣3）（2x﹣y+3）．
【答案】见试题解答内容
【分析】利用平方差公式和完全平方公式解答．
【解答】解：原式＝[2x+（y﹣3）][2x﹣（y﹣3）]
＝4x2﹣（y﹣3）2
＝4x2﹣（y2﹣6y+9）
＝4x2﹣y2+6y﹣9．
23．（5分）运用整式乘法公式进行计算：20242﹣2023×2025．
【答案】1．
【分析】利用平方差公式进行简便运算即可．
【解答】解：原式＝20242﹣（2024﹣1）×（2024+1）
＝20242﹣20242+1
＝1．
24．（5分）因式分解：2x2（a+b）2﹣2xy（a+b）2﹣12y2（﹣a﹣b）2．
【答案】2（a+b）2（x+2y）（x﹣3y）．
【分析】先提取公因式，再利用十字相乘法分解即可．
【解答】解：原式＝2x2（a+b）2﹣2xy（a+b）2﹣12y2（a+b）2
＝2（a+b）2（x2﹣xy﹣6y2）
＝2（a+b）2（x+2y）（x﹣3y）．
四、解答题（本大题共4题，25题7分，26，27题每题8分，28题5分，满分28分）
25．（7分）先化简，再求值：（9an+2+6a3n﹣1﹣an）÷（﹣6an﹣1）+（﹣an+1）2÷（﹣a）2（n为正整数），其中a＝﹣2．
【答案】﹣a3+a，11．
【分析】先根据多项式除单项式和单项式除单项式法则算除法，再合并同类项，化简后将a＝﹣2代入计算即可．
【解答】解：（9an+2+6a3n﹣1﹣an）÷（﹣6an﹣1）+（﹣an+1）2÷（﹣a）2
＝﹣a3﹣a2n+a+a2n
＝﹣a3+a，
当a＝﹣2时，
原式＝﹣×（﹣2）3+×（﹣2）
＝﹣×（﹣8）﹣
＝12﹣
＝11．
26．（8分）已知A＝b2﹣a2+5ab，B＝3ab+2b2﹣a2．
（1）化简：3A﹣B；
（2）已知a、b满足（a+1）2+|b+2|＝0，求3A﹣B的值．
【答案】（1）﹣2a2+12ab+b2；
（2）26．
【分析】（1）把A与B代入原式，去括号合并即可得到结果；
（2）利用非负数的性质求出a与b的值，代入原式计算即可求出值．
【解答】解：（1）∵A＝b2﹣a2+5ab，B＝3ab+2b2﹣a2，
∴3A﹣B＝3（b2﹣a2+5ab）﹣（3ab+2b2﹣a2）＝3b2﹣3a2+15ab﹣3ab﹣2b2+a2＝﹣2a2+12ab+b2；
（2）∵（a+1）2+|b+2|＝0，
∴a＝﹣1，b＝﹣2，
则原式＝﹣2×1+12×（﹣1）×（﹣2）+4
＝﹣2+24+4
＝26．
27．（8分）图1是一个长方形窗户ABCD，它是由上下两个长方形（长方形AEFD和长方形EBCF）的小窗户组成，在这两个小窗户上各安装了一个可以朝一个方向水平方向拉伸的遮阳帘，这两个遮阳帘的高度分别是a和2b（即DF＝a，BE＝2b），且b＞a＞0．当遮阳帘没有拉伸时（如图1），窗户的透光面积就是整个长方形窗户（长方形ABCD）的面积．
如图2，上面窗户的遮阳帘水平方向向左拉伸2a至GH．当下面窗户的遮阳帘水平方向向右拉伸2b时，恰好与GH在同一直线上（即点G、H、P在同一直线上）．
（1）求长方形窗户ABCD的总面积；（用含a、b的代数式表示）
（2）如图3，如果上面窗户的遮阳帘保持不动，将下面窗户的遮阳帘继续水平方向向右拉伸b至PQ时，求此时窗户透光的面积（即图中空白部分的面积）为多少？（用含a、b的代数式表示）
附加题：（3）如果上面窗户的遮阳帘保持不动，当下面窗户的遮阳帘拉伸至BC的中点处时，请通过计算比较窗户的透光的面积与被遮阳帘遮住的面积的大小．
【答案】见试题解答内容
【分析】（1）根据题意，可以用a、b的代数式表示出AB、AD，然后即可计算出长方形窗户ABCD的总面积；
（2）根据题意，可以计算出AE、AG、CF、CP，然后即可计算出窗户透光的面积；
（3）根据题意和图形，可以分别计算出窗户的透光的面积与被遮阳帘遮住的面积，然后作差比较即可．
【解答】解：（1）由题意可得，
AD＝2a+2b，AB＝a+2b，
∴长方形窗户ABCD的总面积是AD•AB＝（2a+2b）（a+2b）＝2a2+6ab+4b2，
即长方形窗户ABCD的总面积是2a2+6ab+4b2；
（2）由图3可得，
AG＝2b，AE＝a，CF＝2b，CP＝（2a+2b）﹣（2b+b）＝2a﹣b，
则窗户透光的面积是：AG•AE+CF•CP
＝2b•a+2b（2a﹣b）
＝2ab+4ab﹣2b2
＝6ab﹣2b2；
（3）当上面窗户的遮阳帘保持不动，下面窗户的遮阳帘拉伸至BC的中点处时，窗户透光的面积是：2b•a+2b（a+b）＝2ab+2ab+2b2＝4ab+2b2，
被遮阳帘遮住的面积是：（2a2+6ab+4b2）﹣（4ab+2b2）
＝2a2+6ab+4b2﹣4ab﹣2b2
＝2a2+2ab+2b2，
（4ab+2b2）﹣（2a2+2ab+2b2）
＝4ab+2b2﹣2a2﹣2ab﹣2b2
＝﹣2a2+2ab
＝2a（b﹣a），
∵b＞a＞0，
∴b﹣a＞0，
∴2a（b﹣a）＞0，
即窗户的透光的面积大于被遮阳帘遮住的面积．
28．（5分）在3×3的方格中，每行、每列及对角线上的3个代数式的和都相等，我们把这样的方格图叫做“等和格”，如图1的“等和格”中，每行、每列及对角线上的3个代数式的和都等于15．
（1）在图2的“等和格”方格图中，可得a＝ ﹣b （用含b的代数式表示）：
（2）在图3的“等和格”方格图中，可得a＝ ﹣2 ，b＝ 2 ；
（3）在图4的“等和格”方格图中，可得b＝ ﹣9 ．
【答案】（1）﹣b；
（2）﹣2；2；
（3）﹣9．
【分析】（1）根据“等和格”的定义，即可得出﹣2a+a＝3b+2a，变形后即可用含b的代数式表示出a；
（2）根据“等和格”的定义，即可得出关于a，b的二元一次方程组，解之即可求出a，b的值；
（3）根据“等和格”的定义，即可得出关于a，b的二元二次方程组，方程①变形后可得出方程③，方程②变形后可得出方程④，再将③代入④中即可求出b的值．
【解答】解：（1）依题意得：﹣2a+a＝3b+2a，
∴a＝﹣b．
故答案为：﹣b．
（2）依题意得：，
解得：．
故答案为：﹣2；2．
（3）依题意得：，
由①可得：a2+a＝3③，
由②可得：b＝﹣2a2﹣2a﹣3④，
将③代入④中得：b＝﹣2（a2+a）﹣3＝﹣2×3﹣3＝﹣9．
故答案为：﹣9．
声明：试题解析著作权属所有，未经书面同意，不得复制发布日期：2024/11/23 0:26:40；用户：18328501451；邮箱：18328501451；学号：43314264