湖北省武汉市黄陂区七校联盟2021-2022学年八年级（下）质检数学试卷（3月份）

这是一份湖北省武汉市黄陂区七校联盟2021-2022学年八年级（下）质检数学试卷（3月份），共18页。试卷主要包含了下列运算正确的是，下列命题中，假命题是，水深和芦苇长各多少尺？等内容，欢迎下载使用。

1.（3分）使式子a-2有意义的a的取值范围是( )
A. a>2B. a⩾2C. a≠2D. a⩽2
2.（3分）下列二次根式中属于最简二次根式的是()
A. 12B. 1.5C. 25D. 26
3.（3分）下列几组数中，不能作为直角三角形三边长的是( )
A. 5，12，13B. 9，40，41
C. 3，4，5D. 2，3，4
4.（3分）如图，组成正方形网格的小正方形边长为1，那么点A表示的数为( )
A. 10B. 11C. 12D. 13
5.（3分）下列运算正确的是( )
A. 2+3=5B. 33-3=3C. 24÷6=4D. 3×5=15
6.（3分）把m-1m根号外的因式移入根号内得( )
A. mB. -mC. -mD. --m
7.（3分）下列命题中，假命题是( )
A. 一个三角形三条边确定，那么这个三角形的形状就被唯一确定
B. 如果两个三角形的面积和周长都相等，那么这两个三角形全等
C. 等腰三角形底边上的中线平分顶角
D. 三角形外角可以是一个锐角
8.（3分）如图是医院、公园和超市的平面示意图，超市在医院的南偏东25°的方向，且到医院的距离为300m，公园到医院的距离为400m，若公园到超市的距离为500m，则公园在医院的( )

A. 北偏东75°的方向上B. 北偏东65°的方向上
C. 北偏东55°的方向上D. 无法确定
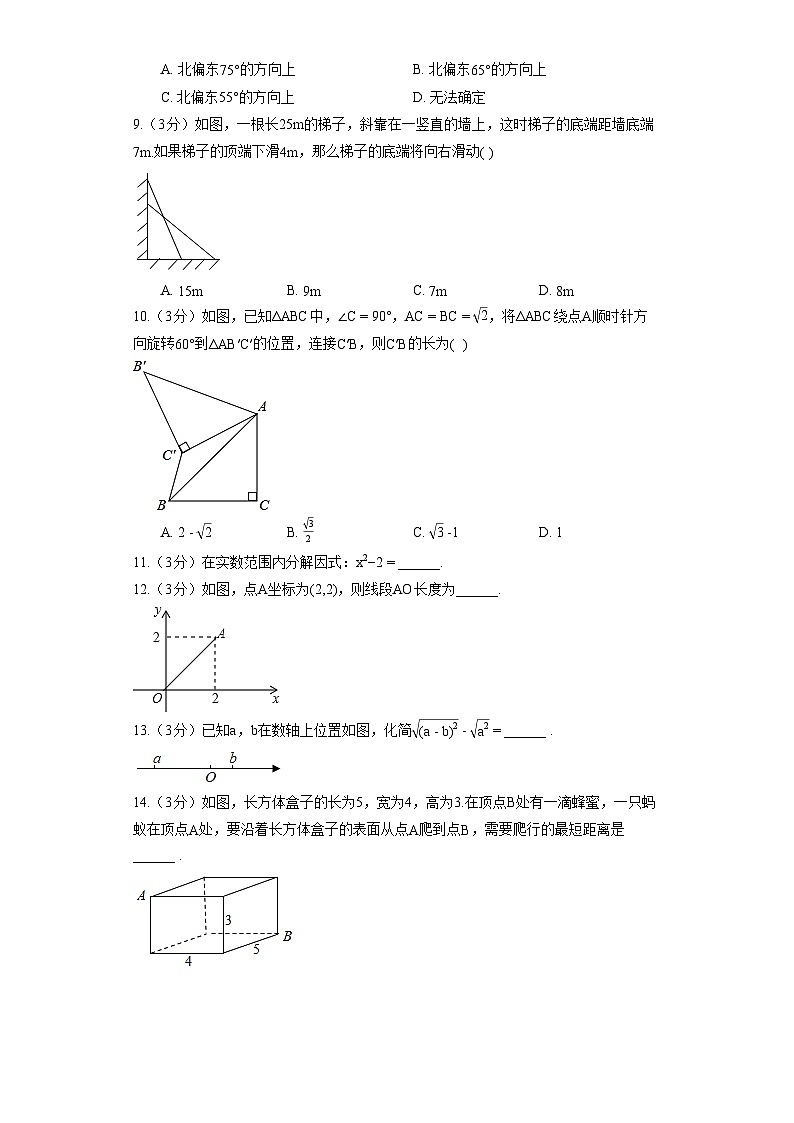
9.（3分）如图，一根长25m的梯子，斜靠在一竖直的墙上，这时梯子的底端距墙底端7m.如果梯子的顶端下滑4m，那么梯子的底端将向右滑动( )
A. 15mB. 9mC. 7mD. 8m
10.（3分）如图，已知ΔABC中，∠C=90°，AC=BC=2，将ΔABC绕点A顺时针方向旋转60°到ΔAB′C′的位置，连接C′B，则C′B的长为( )
A. 2-2B. 32C. 3-1D. 1
11.（3分）在实数范围内分解因式：x2−2=______.
12.（3分）如图，点A坐标为(2,2)，则线段AO长度为______.
13.（3分）已知a，b在数轴上位置如图，化简(a-b)2-a2=______ .
14.（3分）如图，长方体盒子的长为5，宽为4，高为3.在顶点B处有一滴蜂蜜，一只蚂蚁在顶点A处，要沿着长方体盒子的表面从点A爬到点B，需要爬行的最短距离是 ______ .
15.（3分）如图，在平面直角坐标系中，矩形OABC的顶点A，C的坐标分别为(5,0)，(0,3)，点P在BC边上运动，当ΔOAP是等腰三角形时，点P的坐标为______.
16.（3分）如图，在ΔABC中，∠ACB=90°，AC=BC=6cm，D是AB的中点，点E在AC上，过点D作DF⊥DE，交BC于点F.如果AE=2cm，则四边形CEDF的周长是 ______ cm.
17.（8分）计算：
(1)12-3+13；
(2)48÷3-12×12+24.
18.（8分）已知a=2+3，b=2-3，求下列各式的值：
(1)a2+b2；
(2)ab-ba.
19.（8分）《九章算术》中有一道“引葭赴岸”问题：“今有池一丈，葭生其中央，出水一尺，引葭赴岸，适与岸齐.问水深，葭长各几何？”
题意是：有一个池塘，其底面是边长为10尺的正方形，一棵芦苇AB生长在它的中央，高出水面部分BC为1尺.如果把该芦苇沿与水池边垂直的方向拉向岸边，那么芦苇的顶部B恰好碰到岸边的B'(如图).水深和芦苇长各多少尺？
20.（8分）如图所示的正方形网格中，每个小正方形的边长为1.
求：(1)求ΔABC的周长；
(2)判断ΔABC的形状，并说明理由．
21.（8分）如图，公路MN和公路PQ在P点处交汇，点A处有一所中学，AP=160米，∠NPQ=30°，拖拉机的速度是5米/秒，拖拉机行驶时周围100米以内会受到噪音影响，那么拖拉机在公路MN上沿PN方向行驶时学校是否会受到影响，请说明理由；若受到影响，那么学校受到的影响的时间为多少秒？
22.（8分）已知x=12-3，y=12+3，求x-yx-y的值．
23.（8分）在数学课外学习活动中，小明和他的同学遇到一道题：
已知a=12+3，求2a2-8a+1的值.他是这样解答的：
∵a=12+3=2-3(2+3)(2-3)=2-3，
∴a-2=-3.
∴(a-2)2=3，a2-4a+4=3.
∴a2-4a=-1.
∴2a2-8a+1=2(a2-4a)+1=2×(-1)+1=-1.
请你根据小明的解题过程，解决如下问题：
(1)13+2=______ ；
(2)化简12+1+13+2+14+3+……+1169+168；
(3)若a=15-2，求a4-4a3-4a+3的值.
24.（8分）在平面直角坐标系中，点A、B分别在x、y轴上，且AB=BC，∠ABC=90°，点A(a,0)、B(0,b)，且a、b满足(a+3)2+|b-2|=0．

(1)如图1，则a= ______ ，b= ______ ，点C的坐标为 ______ ；
(2)如图2，若E点在x轴的正半轴上，且满足∠OBC-∠ABO=2∠OBE，CG⊥OB于点G，交BE于点H，求证：CH=BG+OE；
(3)在(2)条件下，请同学们探究线段OG、OE、GH之间的数量关系，并加以证明．
答案和解析
1.【答案】B
【解析】解：式子a-2有意义，则a-2⩾0，
解得：a⩾2.
故选：B.
直接利用二次根式的有意义的条件分析得出答案．
此题主要考查了二次根式有意义的条件，正确把握定义是解题关键．
2.【答案】D
【解析】解：A、12=23，所以12不是最简二次根式；
B、1.5=32=62，所以1.5不是最简二次根式；
C、25=5，所以25不是最简二次根式；
D、26是最简二次根式．
故选：D.
根据最简二次根式的概念判断即可
此题主要考查的是最简二次根式的概念，被开方数不含分母、被开方数中不含能开得尽方的因数或因式的二次根式，叫做最简二次根式．
3.【答案】D
【解析】解：A.∵52+122=132，
∴以5，12，13为边能组成直角三角形，故本选项不符合题意；
B.∵92+402=412，
∴以9，40，41为边能组成直角三角形，故本选项不符合题意；
C.∵32+42=52，
∴以3，4，5为边能组成直角三角形，故本选项不符合题意；
D.∵22+32≠42，
∴以2，3，4为边不能组成直角三角形，故本选项符合题意；
故选：D.
先分别求出两小边的平方和和最长的边的平方，再看看是否相等即可．
此题主要考查了勾股定理的逆定理，注意：如果一个三角形的两边a、b的平方和等于第三边c的平方，那么这个三角形是直角三角形．
4.【答案】A
【解析】解：由勾股定理得，点A表示的数=32+12=10，
故选：A．
根据勾股定理计算，得到答案．
该题考查的是勾股定理，如果直角三角形的两条直角边长分别是a，b，斜边长为c，那么a2+b2=c2．
5.【答案】D
【解析】解：A.2与3不能合并，所以A选项不符合题意；
B.原式=23，所以B选项不符合题意；
C.原式=24÷6=4=2，所以C选项不符合题意；
D.原式=3×5=15，所以D选项符合题意；
故选：D.
根据二次根式的加减法对A、B进行判断；根据二次根式的除法法则对C进行判断；根据二次根式的乘法法则对D进行判断．
此题主要考查了二次根式的混合运算，熟练掌握二次根式的性质、二次根式的乘法和除法法则是解决问题的关键．
6.【答案】D
【解析】解：∵m-1m成立，
∴-1m>0，即m|b|，
∴a-b