湖北省武汉市武昌区南湖中学2021-2022学年八年级（上）月考数学试卷（12月份）

这是一份湖北省武汉市武昌区南湖中学2021-2022学年八年级（上）月考数学试卷（12月份），共18页。试卷主要包含了下列图案中，是轴对称图形的是，下列运算中正确的是，用科学记数法表示数0，下列因式分解正确的是等内容，欢迎下载使用。

1.（3分）下列图案中，是轴对称图形的是( )
A. B.
C. D.
2.（3分）使分式13-x有意义的x的取值范是( )
A. x≠3B. x=3C. x≠0D. x=0
3.（3分）下列运算中正确的是( )
A. x2⋅x3=x6B. (x+1)2=x2+1
C. (-2x2)3=-2x6D. a8÷a2=a6
4.（3分）如图，已知AB=AD，那么添加下列一个条件后，仍无法判定ΔABC≌ΔADC的是( )
A. CB=CDB. ∠BAC=∠DACC. ∠BCA=∠DCAD. ∠B=∠D=90°
5.（3分）用科学记数法表示数0.000012，正确的是( )
A. 12×104B. 1.2×105
C. 12×10-4 D. 1.2×10-5
6.（3分）下列因式分解正确的是( )
A. x2-2x-8=x(x-2)-8
B. a4-1=(a2+1)(a2-1)
C. 4x2-1=(4x+1)(4x-1)
D. -x2+4xy-4y2=-(x-2y)2
7.（3分）若等腰三角形的周长为30cm，一边为14cm，则腰长为( )

A. 2cm B. 8cmC. 8cm或2cmD. 14cm或8cm
8.（3分）对于任何整数m，多项式(4m+5)2-9都能( )
A. 被8整除B. 被m整除
C. 被(m-1)整除D. 被(2m-1)整除
9.（3分）如图△ABC中，∠A=36°，AB=AC，BF平分∠ABC，E是AF的中点，DE⊥AC交AB于D，连接DC交BF于P，∠DPB的度数是()
A. 36°B. 54°C. 72°D. 90°
10.（3分）如图，等边ΔABC中，BF是AC边上中线，点D在BF上，连接AD，在AD的右侧作等边ΔADE，连接EF，当ΔAEF周长最小时，∠CFE的大小是( )
A. 30°B. 45°C. 60°D. 90°
11.（3分）若分式x2-1x+1的值为0，则x=______．
12.（3分）若n边形的内角和等于外角和的2倍，则边数n为______．
13.（3分）已知4x2−12xy+(ny)2是完全平方式，则n的值为 ______.
14.（3分）如图，AD⊥BC于D，且DC=AB+BD，若∠BAC=108°，则∠C的度数是______度．
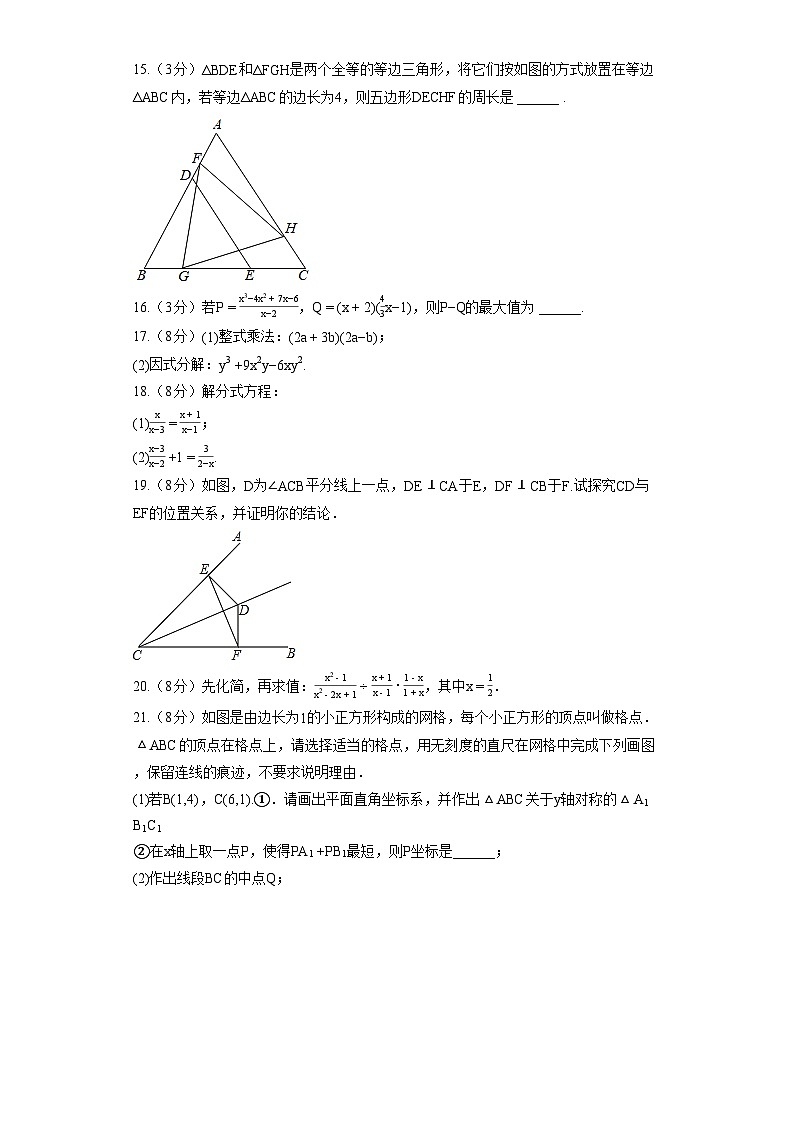
15.（3分）ΔBDE和ΔFGH是两个全等的等边三角形，将它们按如图的方式放置在等边ΔABC内，若等边ΔABC的边长为4，则五边形DECHF的周长是 ______ .
16.（3分）若P=x3−4x2+7x−6x−2，Q=(x+2)(43x−1)，则P−Q的最大值为 ______.
17.（8分）(1)整式乘法：(2a+3b)(2a−b)；
(2)因式分解：y3+9x2y−6xy2.
18.（8分）解分式方程：
(1)xx−3=x+1x−1；
(2)x−3x−2+1=32−x.
19.（8分）如图，D为∠ACB平分线上一点，DE⊥CA于E，DF⊥CB于F.试探究CD与EF的位置关系，并证明你的结论．
20.（8分）先化简，再求值：x2-1x2-2x+1÷x+1x-1⋅1-x1+x，其中x=12．
21.（8分）如图是由边长为1的小正方形构成的网格，每个小正方形的顶点叫做格点．△ABC的顶点在格点上，请选择适当的格点，用无刻度的直尺在网格中完成下列画图，保留连线的痕迹，不要求说明理由．
(1)若B(1,4)，C(6,1).①．请画出平面直角坐标系，并作出△ABC关于y轴对称的△A1B1C1
②在x轴上取一点P，使得PA1+PB1最短，则P坐标是______；
(2)作出线段BC的中点Q；
(3)点M是格点、且MB=MC，则M点有______个
22.（8分）一辆汽车开往距离出发地180km的目的地，出发后第一小时内按原计划的速度匀速行驶，一小时后以原来速度的1.5倍匀速行驶，并比原计划提前40min到达目的地，设前一小时行驶的速度为xkm/h．
(1)直接用x的式子表示提速后走完剩余路程的时间为______h.
(2)求汽车实际走完全程所花的时间；
(3)若汽车按原路返回，司机准备一半路程以mkm/h的速度行驶，另一半路程以nkm/h的速度行驶(m≠n)，朋友提醒他一半时间以mkm/h的速度行驶，另一半时间以nkm/h的速度行驶更快，你觉得谁的方案更快？请说明理由．
23.（8分）已知：ΔABC中，∠ACB=90°，AC=BC．
(1)如图1，点D在BC的延长线上，连AD，过B作BE⊥AD于E，交AC于点F.求证：AD=BF；
(2)如图2，点D在线段BC上，连AD，过A作AE⊥AD，且AE=AD，连BE交AC于F，连DE，问BD与CF有何数量关系，并加以证明；
(3)如图3，点D在CB延长线上，AE=AD且AE⊥AD，连接BE、AC的延长线交BE于点M，若AC=3MC，请直接写出DBBC的值．
24.（8分）平面直角坐标系中，已知：A(a,0)，B(0,b)，且a、b满足a2-4a+8=4b-b2
(1)求出A、B两点的坐标；
(2)如图，P、N为x轴上两动点，且始终满足AP=ON，过O作NB的垂线交AB的延长线于M，连接MP，求证：NB+OM=MP；
(3)如图，点C在y轴的正半轴上，点A关于y轴的对称点为点D，点Q，G分别是边DC和AC上的动点，且满足DQ+AG=AD，连接QG，QG的垂直平分线交x轴于点H，连接QH、HG，试判断∠QHG和∠DCA之间的关系，并给出证明．
答案和解析
1.【答案】C
【解析】解：A、不是轴对称图形，故本选项不合题意；
B、不是轴对称图形，故本选项不合题意；
C、是轴对称图形，故本选项符合题意；
D、不是轴对称图形，故本选项不合题意；
故选：C．
根据轴对称图形的概念判断．
此题主要考查的是轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．
2.【答案】A
【解析】解：分式13-x有意义，则3-x≠0，
解得：x≠3．
故选：A．
直接利用分式有意义的条件进而得出答案．
此题主要考查了分式有意义的条件，正确把握分式的定义是解题关键．
3.【答案】D
【解析】
该题考查了同底数幂相乘，完全平方公式，积的乘方及同底数幂相除等知识点，掌握好运算法则是解答该题的关键．
根据同底数幂相乘，底数不变，指数相加；完全平方公式；积的乘方等于把积的每一个因式分别乘方，再把所得的幂相乘；同底数幂相除底数不变，指数相减；对各项逐一计算便可得出结果．

解：∵x2⋅x3=x5，故选项A错误，
∵(x+1)2=x2+2x+1，故选项B错误，
∵(-2x2)3=-8x6，故选项C错误，
∵a8÷a2=a6，故选项D正确，
故选：D．

4.【答案】C
【解析】
该题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL.注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．
解：A、添加CB=CD，根据SSS，能判定ΔABC≌ΔADC，故A选项不符合题意；
B、添加∠BAC=∠DAC，根据SAS，能判定ΔABC≌ΔADC，故B选项不符合题意；
C、添加∠BCA=∠DCA时，不能判定ΔABC≌ΔADC，故C选项符合题意；
D、添加∠B=∠D=90°，根据HL，能判定ΔABC≌ΔADC，故D选项不符合题意．
故选C．
5.【答案】D
【解析】解：用科学记数法表示数0.000012，正确的是1.2×10-5．
故选：D．
绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10-n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．
该题考查用科学记数法表示较小的数，一般形式为a×10-n，其中1⩽|a|