2023-2024学年福建省泉州一中九年级（上）期末数学试卷

这是一份2023-2024学年福建省泉州一中九年级（上）期末数学试卷，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

（全卷满分：150分 考试时间：120分钟）
一、选择题：本题共10小题，每小题4分，共40分。在每小题给出的四个选项中，只有一项是符合要求的。在答题卡相应的答题区域内作答。
1．下列选项中是一元二次方程的是（ ）．
A． B．
C． D．
2．计算的值等于（ ）．
A． B．1 C． D．
3．下列事件中，属于必然事件的是（ ）．
A．泉州明天会下大雨 B．在369个人中，一定有两个人在同日出生
C．打开电视机，正好在播新闻 D．小明这学期数学期末考试得分是146
4．下列二次根式中，能与合并的是（ ）．
A． B． C． D．
5．用配方法解一元二次方程，下列变形结果正确的是（ ）
A． B． C． D．
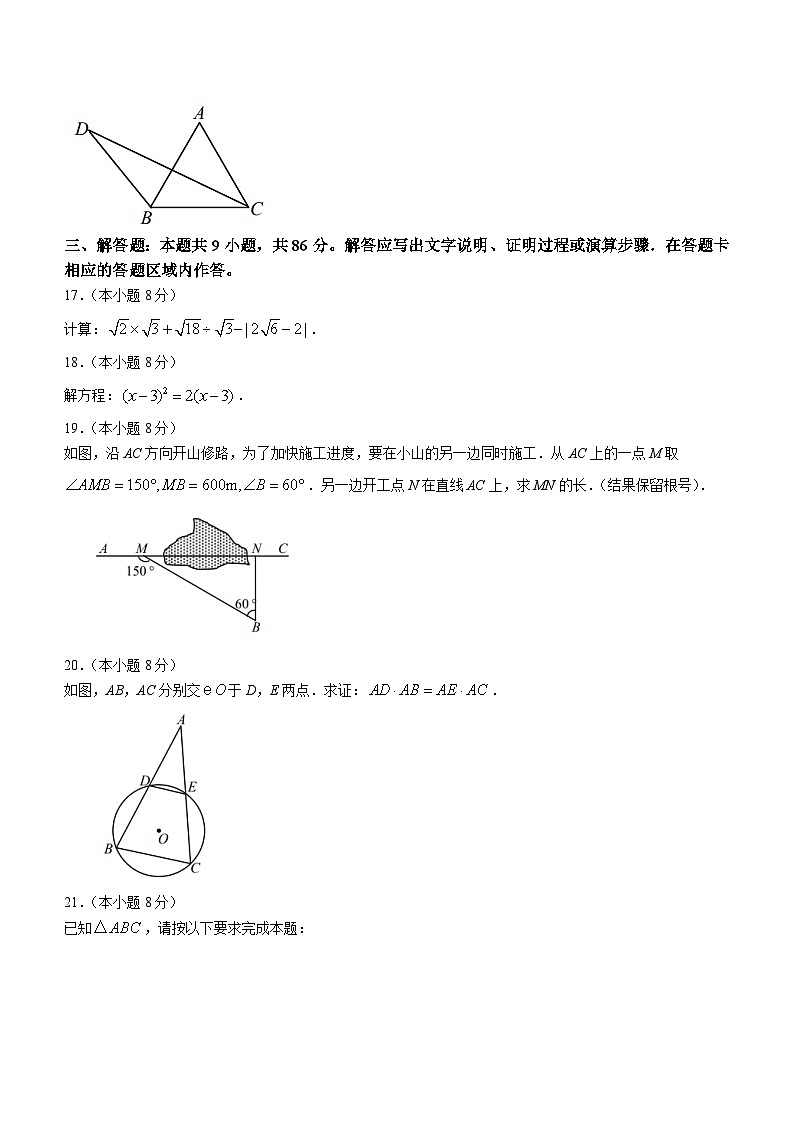
6．如图，D是边AB上一点，添加一个条件后，仍不能使的是（ ）
A． B． C． D．
7．抛物线经过平移得到抛物线，则平移过程正确的是（ ）．
A．先向左平移4个单位，再向下平移3个单位 B．先向左平移4个单位，再向上平移3个单位
C．先向右平移4个单位，再向下平移3个单位 D．先向右平格4个单位，再向上平移3个单位
8．如图，若与是位似图形，则位似中心的坐标为（ ）
A． B． C． D．
9．如图，点A，B，C在半径为5的上，，则的值为（ ）．
A． B． C． D．
10．已知抛物线的顶点为，点在该抛物线上，当恒成立时，的最小值为（ ）．
A．1 B．2 C．3 D．4
二、填空题：本题共6小题，每小题4分，共24分。在答题卡相应的答题区域内作答。
11．式子在实数范围内有意义，则x的取值范围是__________．
12．已知，则__________．
13．一只盒子中有红球10个，白球6个，黑球a个，每个球除颜色外都相同，从中任取一个球，取得“红球”的概率与“不是红球”的概率相同，那么a的值是__________．
14．若直线l上有四点A，B，C，D，直线l外有一点P，则经过图中的三个点作圆，最多可以作__________个．
15．一个等腰三角形的底边长是6，腰长是一元二次方程的一个根，则此三角形的周长是__________．
16．如图，为等边三角形，点D在外，连接BD、CD．若，，，则__________．
三、解答题：本题共9小题，共86分。解答应写出文字说明、证明过程或演算步骤．在答题卡相应的答题区域内作答。
17．（本小题8分）
计算：．
18．（本小题8分）
解方程：．
19．（本小题8分）
如图，沿AC方向开山修路，为了加快施工进度，要在小山的另一边同时施工．从AC上的一点M取．另一边开工点N在直线AC上，求MN的长．（结果保留根号）．
20．（本小题8分）
如图，AB，AC分别交于D，E两点．求证：．
21．（本小题8分）
已知，请按以下要求完成本题：
（1）请作出的外接圆（尺规作图，保留作图痕迹）：（4分）
（2）若在中，的直径AD交CB于E，求的度数．（4分）
22．（本小题10分）
一个不透明的纸箱里有三张完全相同的卡片，它们上面分别写着，小丽从中抽取一张，看完数后，把卡片放回，搅均，然后小明再从中抽取一张．
（1）直接写出小丽取出的卡片恰好是的概率；（2分）
（2）同学小颖帮他们设计了一个游戏规则：若两人抽取卡片上的数字之积为有理数，则小丽获胜：否则小明获胜．你认为这个游戏规则公平吗？若不公平，则对谁有利？请说明理由．（8分）
23．（本小题10分）
如图，用一段80米的篱笆围成三个一边靠墙、大小相同的长方形羊圈，左右两个长方形都有一个1米的门通往中间长方形，中间的长方形有一个1米的门通往外面，墙的最大可用长度为50米．
（1）如果羊圈的总面积为345平方米，求边AB的长；（7分）
（2）请问羊圈的总面积能为480平方米吗？若能，请求出边AB的长；若不能，请说明理由．（3分）
24．（本小题12分）
如图，是的外接圆，BC为的直径，点I为的内心，连接AI并延长交于D点，连接BD并延长至E，使得，连接CE、BI．
（1）求证：；（4分）
（2）求证：直线CE为的切线；（4分）
（3）若，求AD的长．（4分）
25．（本小题14分）
抛物线与x轴只有一个交点，与直线交于B，C两点，点C恰好落在y轴上．
（1）直接写出此抛物线的解析式：（3分）
（2）在抛物线的对称轴右侧图象上存在两点，且，直线PC和直线QB与抛物线的对称轴的分别交于点D和点E．
①求的最大值；（5分）
②若直线，求证：的面积是一个定值．（6分）
2023-2024学年上学期九年级期末考试
数学试题参考答案及评分标准
（全卷满分：150分考试时间：120分钟）
一、选择题：本题共10小题，每小题4分，共40分。在每小题给出的四个选项中，只有一项是符合要求的。在答题卡相应的答题区域内作答。
二、填空题：本题共6小题，每小题4分，共24分。在答题卡相应的答题区域内作答。
11． 12．5 13．4
14．6 15．14 16．11
三、解答题：本题共9小题，共86分。解答应写出文字说明、证明过程或演算步骤。在答题卡相应的答题区域内作答。
17．（本小题8分）
解：原式 6分
． 8分
18．（本小题8分）
解：原方程化为： 2分
6分
． 8分
19．（本小题8分）
解：
又
2分
4分
在中
故MN的长为． 8分
20．（本小题8分）
证明：B，C，E，D四点都在上，
即四边形BCED为的内接四边形
2分
又
4分，
6分
，即． 8分
21．（本小题8分）
解：（1）如图所示为所求作的的外接圆； 4分
（2）连接BD．
是的直径， 5分
又
6分
又
，故的度数为． 8分
22．（本小题10分）
解：（1）依题意得：P（小丽取出的卡片恰好是）； 2分
（2）列表如下：
6分
从表格中可以看出共有9个等可能的结果，而数字之积为有理数有5个 7分
∴P（小丽获胜），P（小明获胜） 9分
对小丽有利． 10分
23．（本小题10分）
解：（1）设边AB的长为x，依题意得：
3分
整理得：
解得：
当时，，不合题意
答：边AB的长为15米； 7分
（2）设边AB的长为x，依题意得：
整理得：
∴此方程无解，故羊圈的总面积不能为480平方米． 10分
24．（本小题12分）
（1）证明：点I为的内心
又
； 3分
； 4分
（2）证明：连接CD，如图所示．
由（1）得：
则
，即 7分
又BC为的直径
直线CE为的切线： 8分
（3）解析：为的直径
为直角三角形
不妨设
则有，解得：
9分
过点I作交AC于点H，如图所示．
的半径 10分
由（2）得：
同理可得：
故AD的长为． 12分
25．（本小题14分）
解：（1）此抛物线的解析式为； 3分
（2）①由（1）得
∴此抛物线的对称轴为直线，
如图，设的外心为点F，过点F作于点G，连接FO，FC，FD
则
在中，
∴当时，随着FG的增大而减小
∴当FG最小时，最大
∴当FD最小时，最小，FG最小，此时直线与相切
则当直线时，D，F，G三点共线
由得：
解得：
的最大值为； 8分
②设点D的纵坐标为t，直线交QC于点
，直线直线BC
点D与点关于直线BC对称
由可得，
联立解方程组，得：
由可得
令得：
的面积是一个定值． 14分 题号
1
2
3
4
5
6
7
8
9
10
答案
A
B
B
D
A
C
B
B
C
C
小丽
小明