2024年中考数学一轮复习：与圆中有关的计算练习

这是一份2024年中考数学一轮复习：与圆中有关的计算练习，共3页。
1. 掌握正多边形的有关概念与计算；
2．掌握弧长公式和扇形面积公式，会计算弧长及扇形面积，并能解决简单的实际问题；
3．了解圆柱、圆锥的底面、高、母线等概念，了解圆锥的侧面展开图是扇形，会进行相关的简单计算.
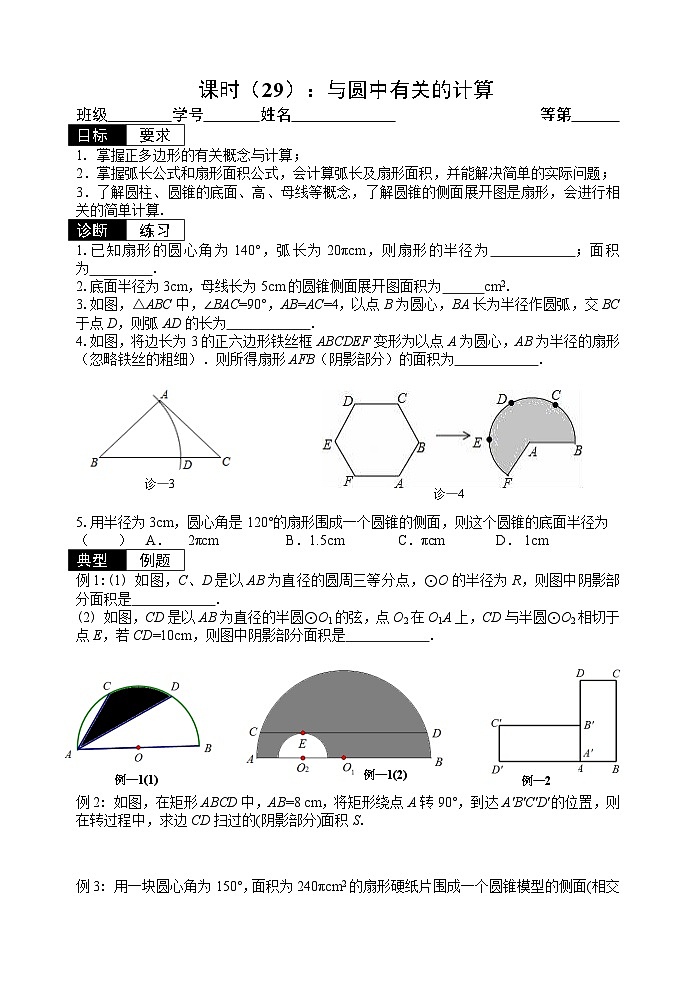
1.已知扇形的圆心角为140°，弧长为20πcm，则扇形的半径为 ；面积为 .
2.底面半径为3cm，母线长为5cm的圆锥侧面展开图面积为 cm2.
3.如图，△ABC中，∠BAC=90°，AB=AC=4，以点B为圆心，BA长为半径作圆弧，交BC于点D，则弧AD的长为 .
4.如图，将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心，AB为半径的扇形（忽略铁丝的粗细）．则所得扇形AFB（阴影部分）的面积为 .
诊—3
诊—4
5.用半径为3cm，圆心角是120°的扇形围成一个圆锥的侧面，则这个圆锥的底面半径为（ ） A．2πcm B．1.5cm C．πcm D．1cm
例1:(1) 如图，C、D是以AB为直径的圆周三等分点，⊙O的半径为R，则图中阴影部分面积是 .
(2) 如图，CD是以AB为直径的半圆⊙O1的弦，点O2在O1A上，CD与半圆⊙O2相切于点E，若CD=10cm，则图中阴影部分面积是 .
例—1(1)
例—1(2)
例—2
例2: 如图，在矩形ABCD中，AB=8 cm，将矩形绕点A转90°，到达AʹBʹCʹDʹ的位置，则在转过程中，求边CD扫过的(阴影部分)面积S.
例3: 用一块圆心角为150°，面积为240πcm2的扇形硬纸片围成一个圆锥模型的侧面(相交粘贴部分忽略不计)，求圆锥模型的底面半径．
例4:如图，在扇形OAB中，∠AOB=90°，半径OA=2，将扇形OAB沿过点B的直线折叠，使点O恰好落在弧AB上的点D处，折痕为BC，求图中阴影部分的面积.
例5:如图，在△ABC中，∠A=90°，O是BC边上一点，以O为圆心的半圆分别与AB、AC边相切于D、E两点，连接OD．已知BD=2，AD=3．
求：（1）tanC；（2）图中两部分阴影面积的和．
班级 学号 姓名 等第
1.边长为a的正六边形对角线的长为 .
2.两个圆锥的母线长相等．侧面积之比为1：2，底面积之比为 ( )
A 2：1 B 1：2 C 1：3 D 1：4
3.一个圆锥的侧面积是底面积的2倍，则这个圆锥的侧面展开扇形的圆心角为_______°.
4.如图，PA、PB切⊙O于A、B，若∠APB＝60°，⊙O半径为3，求阴影部分面积.
5.如图，AB为半圆O的直径，AC是⊙O的一条弦，D为的中点，作DE⊥AC交AB的延长线于点F,连接AD.
（1）求证：EF为半圆O的切线；
（2）若DA=DF=，求阴影区域的面积.（结果保留根号和π）
目标
要求
诊断
练习
典型
例题
课堂
检测