2024年苏科版数学中考一轮复习学案：圆的概念与性质

这是一份2024年苏科版数学中考一轮复习学案：圆的概念与性质，共3页。

1.理解圆及弦、弧、圆心角、圆周角的概念，了解弦、弧、圆心角之间的关系；
2.利用圆的对称性解答相关问题.
1.下列说法错误的是（ ）
A．直径是圆中最长的弦 B．长度相等的两条弧是等弧
C．面积相等的两个圆是等圆 D．半径相等的两个半圆是等弧
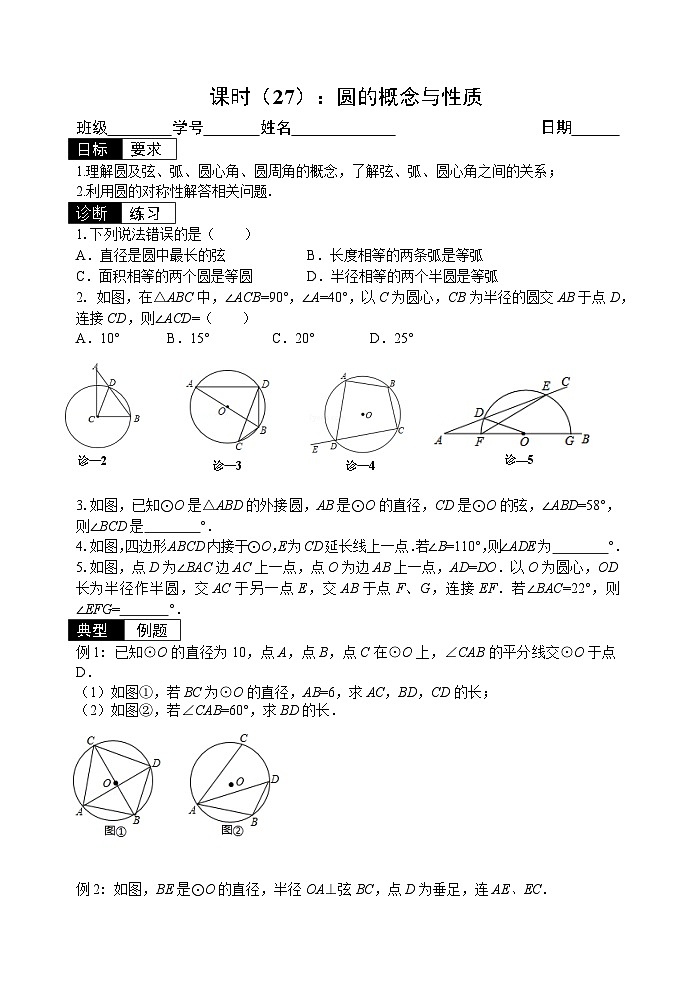
2. 如图，在△ABC中，∠ACB=90°，∠A=40°，以C为圆心，CB为半径的圆交AB于点D，连接CD，则∠ACD=（ ）
A．10° B．15° C．20° D．25°
诊—2
诊—5
诊—4
诊—3

3.如图，已知⊙O是△ABD的外接圆，AB是⊙O的直径，CD是⊙O的弦，∠ABD=58°，则∠BCD是 °．
4.如图，四边形ABCD内接于⊙O，E为CD延长线上一点．若∠B=110°，则∠ADE为 °．
5.如图，点D为∠BAC边AC上一点，点O为边AB上一点，AD=DO．以O为圆心，OD长为半径作半圆，交AC于另一点E，交AB于点F、G，连接EF．若∠BAC=22°，则∠EFG= °．
例1: 已知⊙O的直径为10，点A，点B，点C在⊙O上，∠CAB的平分线交⊙O于点D．
（1）如图①，若BC为⊙O的直径，AB=6，求AC，BD，CD的长；
（2）如图②，若∠CAB=60°，求BD的长．
例2: 如图，BE是⊙O的直径，半径OA⊥弦BC，点D为垂足，连AE、EC．
（1）若∠AEC=28°，求∠AOB的度数；
（2）若∠BEA=∠B，BC=6，求⊙O的半径．
例3:如图，在△ABC中，AB=AC，以AC为直径的⊙O交AB于点D，交BC于点E．
（1）求证：BE=CE； （2）若BD=2，BE=3，求AC的长．
泾河初中初三数学学科作业纸
（内容：圆的概念与性质）
班级 姓名 等第
基础性作业
1.下列语句中，不正确的个数是（ ）
①直径是弦；②弧是半圆；③长度相等的弧是等弧；④三点可以确定一个圆．
A．1个 B．2个 C．3个 D．4个
2.如图，点A、B、C为⊙O上的三个点，∠BOC=2∠AOB，∠BAC=40°，则∠ACB= °．
检—4
检—3
检—2
3.如图，四边形ABCD内接于⊙O，AB=AD，∠C=110°，点E在上，则∠E= °．
4.如图，半径为5的⊙A中，弦BC、ED所对的圆心角分别是∠BAC、∠EAD，若DE=6，
∠BAC+∠EAD=180°.（1）试确定∠B与∠E的数量关系（2）求弦BC的长.
拓展性作业
1.如图，在四边形ABCD中，AD=BC，∠B=∠D，AD不平行于BC，过点C作CE∥AD交△ABC的外接圆O于点E，连接AE．
（1）求证：四边形AECD为平行四边形；（2）连接CO，求证：CO平分∠BCE．
2. 如图，⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F．
（1）若∠E=∠F时，求证：∠ADC=∠ABC；
（2）若∠E=∠F=42°时，求∠A的度数；
（3）若∠E=α，∠F=β，且α≠β．请你用含有α、β的代数式表示∠A的大小．
目标
要求
诊断
练习
典型
例题