第四章整式的加减（单元复习课件）-【大单元教学】2024-2025学年七年级数学上册同步备课系列（人教版2024）

这是一份第四章整式的加减（单元复习课件）-【大单元教学】2024-2025学年七年级数学上册同步备课系列（人教版2024），共35页。

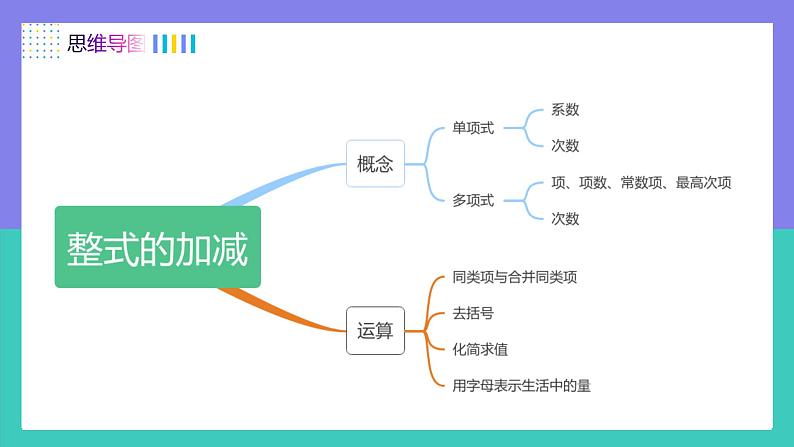
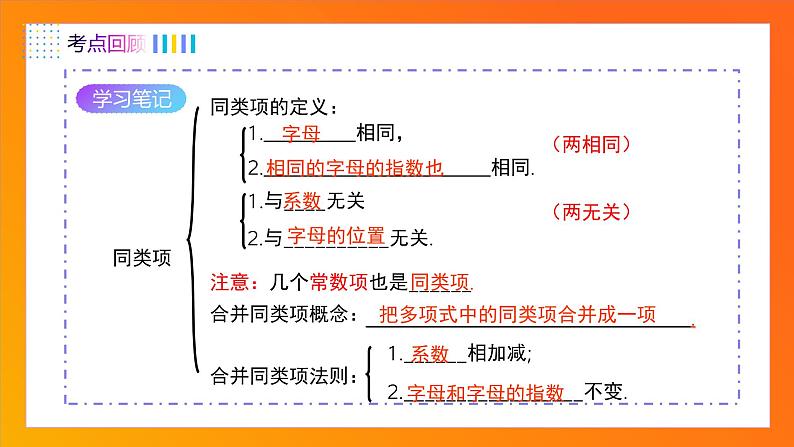
单元复习课整式的加减单项式：定义：系数：次数：由_________________组成的式子.单独的 或 也是单项式.数字或字母的乘积一个数一个字母单项式中的_________.单项式中的__________________.数字因数所有字母的指数和注意的问题：1. 当单项式的系数是 1 或 -1 时，“1”通常省略不写.2. 当式子分母中出现字母时不是单项式.3. 圆周率 π 是常数，不要看成字母.4. 当单项式的系数是带分数时，通常写成假分数.5. 单项式的系数应包括它前面的性质符号.7. 单独的数字不含字母，规定它的次数是零次.6. 单项式次数是指所有字母的次数的和，与数字的次数没有关系.多项式定义：几个__________.项：组成多项式中的_____________. 有几项，就叫做_________.常数项：多项式中_______________.单项式的和每一个单项式几项式不含字母的项多项式中次数最高的项的次数多项式的次数：____________________________. 注意的问题：1. 在确定多项式的项时，要连同它前面的符号.2. 一个多项式的次数最高项的次数是几，就说这个多项式是几次多项式.3. 在多项式中，每个单项式都是这个多项式的项，每一项都有系数，但对整个多项式来说，没有系数的概念，只有次数的概念.同类项同类项的定义：合并同类项概念：合并同类项法则：1. 相同，2. 相同.字母相同的字母的指数也（两相同）1.与____无关2.与__________无关.系数 字母的位置（两无关）注意：几个常数项也是______同类项. .把多项式中的同类项合并成一项1.______相加减;2._________________不变.系数字母和字母的指数整式的加减混合运算步骤(有括号先去括号)（一）去括号(按照先小括号，再中括号，最后大括号的顺序)1. 如果括号外的因数是正数，去括号后原括号内各项的符号与原来的符号相同.2. 如果括号外的因数是负数，去括号后原括号内各项的符号与原来的符号相反.“去括号，看符号.是 ‘+’号，不变号，是‘－’号，全变号”.一、复习回顾（二）计算1. 找同类项，做好标记.2. 利用加法的交换律和结合律把同类项放在一起.3. 利用乘法分配律计算结果.4. 按要求按“升”或“降”幂排列.找搬并排 3. 对于运算结果，常将多项式按某个字母（如 x ）的降幂（升幂）排列.1. 几个整式相加减，如果有括号就先去括号，然后再合并同类项. 2. 整式的加减实际上就是：去括号、合并同类项.例1指出下列单项式的系数和次数：①②④⑦例2练1－xy2的系数 ， －a2b3c5的次数 .A 3个 B 4个 C 5个 D 6个-110B如果-5xym+2为5次单项式,则m=____.2练2练3例1请说出下列各多项式是几次几项式，并写出多项式的最高次项和常数项.下列多项式次数为 3 的是（ ）例2是 次 项式，最高次项是 ，常数项是 ;四三C是 次 项式，最高次项是 ，常数项是 ;四三练1m≠2，n＝3 3 －6 练24 4 a3，－a2b2，ab2，－b3 例1下列合并同类项的结果错误的有 .①、②、③、④、⑤例2合并同类项：(1)解：原式=(2)解：原式=练1合并下列各式的同类项:（1） （2） （3） =-b²+ 2ab(1)解：原式(2)解：原式(3)解：原式练2例1求下列多项式的值：7x2-3x2-2x-2x2+5+6x，其中x=-2；5a-2b+3b-4a-1，其中a=-1， b=2.（1）解：7x2-3x2-2x-2x2+5+6x=7x2-3x2-2x2-2x+6x+5=2x2+4x+5当x=-2时，原式=2×(-2)2+4×(-2)+5=5例1（2）解： 5a-2b+3b-4a-1=5a-4a-2b+3b-1=a+b-1当a=-1， b=2时，原式=-1+2-1=0求下列多项式的值：7x2-3x2-2x-2x2+5+6x，其中x=-2；5a-2b+3b-4a-1，其中a=-1， b=2.练1 若多项式 ，计算多项式A - 2B的值. 练2求下列多项式的值：7x2-3x2-2x-2x2+5+6x，其中x=-2；（1）解 7x2-3x2-2x-2x2+5+6x=7x2-3x2-2x2-2x+6x+5=2x2+4x+5当x=-2时，原式=2×(-2)2+4×(-2)+5=5练1（2）解 5a-2b+3b-4a-1=5a-4a-2b+3b-1=a+b-1当a=-1， b=2时，原式=-1+2-1=0求下列多项式的值：（2）5a-2b+3b-4a-1，其中a=-1， b=2；练1（3）解 2x2-3xy+y2-2xy-2x2+5xy -2y+1=2x2-2x2-3xy-2xy+5xy+y2-2y+1=y2-2y+1求下列多项式的值：(3) 2x2-3xy+y2-2xy-2x3+5xy -2y+1，其中x = ，y =-1.例1化简下列各式解：(1)4a－(a－3b)＝4a－a＋3b＝3a＋3b.(4)5x－y－2(x－y)＝5x－y－(2x－2y)＝5x－y－2x＋2y＝3x＋y.(3)3(2xy－y)－2xy＝6xy－3y－2xy＝4xy－3y.(2)a＋(5a－3b)－(a－2b)＝a＋5a－3b－a＋2b＝5a－b.(1)4a－(a－3b)； (2)a＋(5a－3b)－(a－2b)；(3)3(2xy－y)－2xy； (4)5x－y－2(x－y).例1 先化简，再求值． (1)－(4k3－k2＋5)＋(5k2－k3－4)，其中k＝－2；解： (1) －(4k3－k2＋5)＋(5k2－k3－4) ＝－4k3＋k2－5＋5k2－k3－4＝－5k3＋6k2－9. 当k＝－2时，原式＝－5×(－2)3＋6×(－2)2－9 ＝40＋24－9＝55.例1 先化简，再求值． (2)其中例2已知：A = x2－x+b , B= x2－ax+3 A－B = x+2. 求：a －b.解： ∵ A = x2 －x+b,B = x2 －ax+3 ∴ A－B =(x2－x+b)－(x2－ax+3) = x2－x+b－x2 +ax－3 =(x2－x2 )+(ax－x)+b－3 =(a－1 ) x + b－3又∵ A－B = x + 2 ∴ a －1 = 1 ， b － 3 = 2 ∴ a = 2， b = 5例3有两个多项式： A=2a2 －4a+1, B=(2a2 －2a)+3,当a取任意有理数时，请比较A与B的大小. 解： ∵A－B = (2a2－4a+1 )－ [2(a2－2a)+3] = (2a2 －4a+1 )－ (2a2 －4a+3) = 2a2 －4a+1 － 2a2 +4a－3 = (2a2 － 2a2 )－(4a+4a )+(1－3) = －2<0 ∴ A －B < 0 ∴ A < B练1已知a、b、c如图 所示，化简： ∣a＋c∣＋∣a＋b＋c∣－∣a－b∣＋∣b＋c∣解：由图可知，c