

小学数学七 包装盒--长方体和正方体巩固练习
展开一、选择题(每题2分,共16分)
1.用8个1立方厘米的小正方体拼成一个大正方体,如果拿去一个小正方体(如图),它的表面积与原来的表面积相比,( )。
A.变大了B.变小了
C.不变
2.阳阳把一块棱长是6厘米的正方体橡皮泥捏成长方体形状,如果捏成的长方体长9厘米、宽4厘米,高是( )厘米。
A.6B.5C.12
3.一个棱长为1米的正方体,可以切割成( )个棱长为1分米的正方体。
A.100B.1000C.10000
4.用丝带捆扎一种礼品盒(如图),接头处多余部分长25厘米(接头忽略不计),要捆扎这种礼品盒至少需准备( )分米的丝带。
A.15B.17.5C.22.5
5.下面的四张折纸(每格是正方形),不是正方体表面展开图的是( )。
A.B.C.
6.用棱长2厘米的正方体拼成一个较大的正方体,拼成的正方体的表面积至少是( )平方厘米。
A.216B.96C.24
7.工人叔叔用一根56厘米长的铁丝做一个高3厘米的长方体模型,能做成( )种不同的长方体。(长、宽均为整厘米数)
A.3B.4C.5
8.一根长方体木料长2米,如果把它截成两根同样的1米长的长方体木料,表面积就增加4平方分米,这根木料原来的体积是( )。
A.80立方分米B.40立方分米C.8立方米
二、填空题(每题2分,共16分)
9.一个占地18平方米的长方体蓄水池内有45立方米水,池内水深( )。
10.李师傅想用52厘米长的铁丝做一个高5厘米的长方体模型,能做( )种不同的长方体。
11.一个正方体的棱长之和是60cm,把这个正方体切成两个相同的长方体,一个长方体的体积是( ) SKIPIF 1 < 0 ,这个长方体最大一个面的面积( ) SKIPIF 1 < 0 。
12.一块长8dm,宽6dm,高7dm的大理石,它的占地面积最大是( )dm2。
13.用铁丝围一个长方体框架,相交于一个顶点的三条棱的长度分别是3分米、4分米、5分米,围这个框架需要铁丝( )分米。
14.下面是一个长方体平面展开图(单位:厘米)。这个长方体的体积是( )立方厘米。
15.如图是一个长方体的前面和右面,这个长方体的底面积是( )平方厘米。如果用铁丝制作这个长方体框架,至少需要( )厘米的铁丝。
16.把一个长10厘米、宽和高都是5厘米的长方体切成两个相等的正方体。这两个正方体的表面积之和比原来长方体( );这两个正方体的体积之和与原来长方体相比,( )。(填“大”“小”或“相等”)
三、判断题(每题2分,共8分)
17.体积是100立方分米的油箱,它的容积是100升。( )
18.把一个棱长 SKIPIF 1 < 0 的正方体切成棱长 SKIPIF 1 < 0 的小正方体,可切成100个。( )
19.正方体的棱长扩大2倍,它的体积就扩大8倍。( )
20.如果一个正方体的棱长扩大(缩小)3倍,表面积扩大(缩小)9倍,体积扩大(缩小)27倍.( )
四、计算题(共12分)
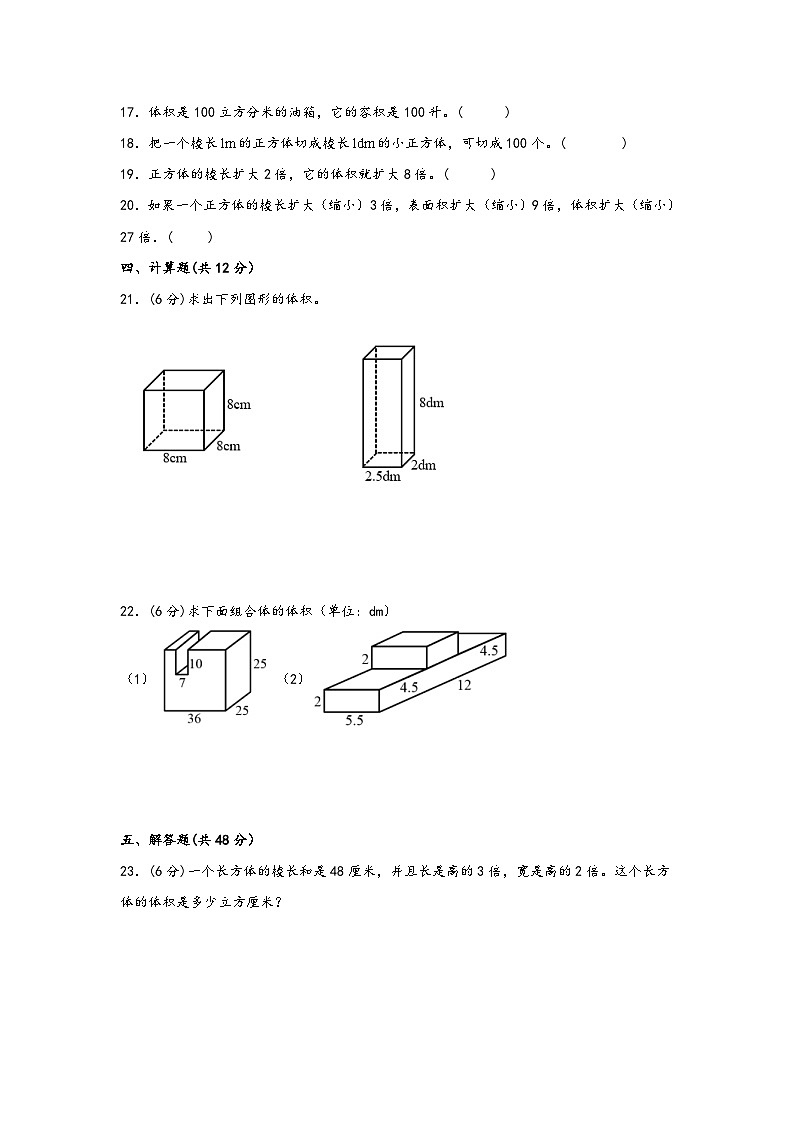
21.(6分)求出下列图形的体积。
22.(6分)求下面组合体的体积(单位:dm)
(1) (2)
五、解答题(共48分)
23.(6分)一个长方体的棱长和是48厘米,并且长是高的3倍,宽是高的2倍。这个长方体的体积是多少立方厘米?
24.(6分)修一道长30米,厚24厘米,高3米围墙。如果每立方米用砖525块,这墙共用砖几块?
25.(6分)烤箱的长是45厘米,宽是30厘米,高是25厘米,李阿姨想把它放进一个长50厘米、宽40厘米,体积是40立方分米的容纳盒里,能装下吗?
26.(6分)一个正方体油桶,从里面量棱长是80厘米。如果1升柴油重0.85千克,这个油桶可以装多少千克柴油?
27.(6分)有一个长方体鱼缸(如图),从里面量长9分米,宽6分米。放进去一块珊瑚石,珊瑚石完全浸没在水中,水面升高了0.5分米。这块珊瑚的体积是多少立方分米?
28.(6分)超市要订做一批环保手提袋,孙强测量了手提袋的尺寸如下图,那么做40个这样的手提袋至少需要多少平方厘米的环保布料?(不考虑粘接处用料)
29.(6分)超市要做一个长2.2米,宽60厘米,高0.8米的玻璃柜台,现要在柜台各个边都安上铝合金条。这个柜台至少需要多少米铝合金条?
30.(6分)月月家鱼缸长50厘米,宽20厘米,高40,鱼缸中水深18厘米,月月买来5块一模一样的彩色石头放入鱼缸来装扮鱼缸,水面上升了2厘米,求每块彩色石头的体积是多少立方厘米?
参考答案
1.C
【分析】通过观察图形可知,原来大正方体的表面积是24个小正方形的面积之和,而拿去一个小正方体后,表面积也是24个小正方形的面积之和;由此得出表面积没有发生变化。据此解答。
【详解】立体图形的表面积与原来的表面积相比,表面积不变。
故答案为:C
【点睛】明确表面积是物体表面的总的面积之和,是解答此题的关键。
2.A
【分析】根据题意,把一块棱长是6厘米的正方体橡皮泥捏成长方体形状,形状变了,体积不变;
先根据正方体的体积=棱长×棱长×棱长,求出这块橡皮泥的体积,也是长方体的体积;再根据长方体的高=体积÷长÷宽,即可求出捏成的长方体的高。
【详解】6×6×6
=36×6
=216(立方厘米)
216÷9÷4
=24÷4
=6(厘米)
捏成的长方体的高是6厘米。
故答案为:A
【点睛】抓住立体图形等积变形中的“体积不变”,先根据正方体的体积公式求出橡皮泥的体积,再灵活运用长方体的体积公式求出长方体的高。
3.B
【分析】根据1米=10分米,先根据正方体的体积=棱长×棱长×棱长,用10×10×10求出棱长为1米的正方体体积,再用1×1×1即可求出棱长1分米的正方体体积,最后根据除法的意义,用棱长为1米的正方体体积除以棱长1分米的正方体体积即可求出切割的个数。
【详解】1米=10分米
10×10×10=1000(立方分米)
1×1×1=1(立方分米)
1000÷1=1000(个)
可以切割成1000个棱长为1分米的正方体.
故答案为:B
【点睛】本题考查了正方体体积公式的应用。
4.C
【分析】结合图示可知,用丝带捆扎这个礼品盒,顺着长的方向有2段、宽的方向有2段、高的方向有4段,又知礼品盒的长宽高分别为30厘米、20厘米、25厘米,且接头处多余部分长25厘米,则要求丝带的总长度可列式:30×2+20×2+25×4+25。
【详解】30×2+20×2+25×4+25
=60+40+100+25
=225(厘米)
=22.5(分米)
故答案为:C
【点睛】关键是能够结合图示确定用丝带捆扎的时候,相当于捆扎了几条长、几条宽、几条高,最后不能忽略接头处多余部分的长度。
5.C
【分析】根据正方体展开图的11种特征,图A、图B是“2-3-1”结构,是正方体的展开图;图C不符合正方体展开图的11种特征,不是正方体的展开图。
【详解】由分析可得:图C不符合正方体展开图的11种特征,不是正方体的展开图。
故答案为:C
【点睛】本题是考查正方体的展开图,培养学生的观察和空间想象能力。
6.B
【分析】用棱长2厘米的正方体拼成一个较大的正方体,较大的正方体的棱长至少是原来正方体棱长的2倍,据此计算出较大正方体的棱长,再利用正方体的表面积计算公式即可求得。
【详解】2×2=4(厘米)
4×4×6
=16×6
=96(平方厘米)
故答案为:B
【点睛】分析题意计算出拼成的正方体的棱长是解答题目的关键。
7.C
【分析】用棱长总和除以4求出一组长、宽、高的和,即56÷4=14厘米,再减去高的长度即可求出长与宽的和,即14-3=11(厘米),则可以是宽1厘米,长是10厘米、宽2厘米,长是9厘米、宽3厘米,长是8厘米、宽4厘米,长是7厘米、宽5厘米,长是6厘米,据此解答即可。
【详解】56÷4-3
=14-3
=11(厘米);
则长和宽可以为:
宽1厘米,长是10厘米;
宽2厘米,长是9厘米;
宽3厘米,长是8厘米;
宽4厘米,长是7厘米;
宽5厘米,长是6厘米;
故答案为:C。
【点睛】先求出一组长、宽、高的和是解答本题的关键,进而求出长与宽的和,再进一步解答。
8.B
【分析】将长方体木料截成两根,表面积增加了两个横截面,求出一个截面面积×长即可。
【详解】2米=20分米
4÷2×20=40(立方分米)
故答案为:B
【点睛】关键是灵活运用长方体体积公式,长方体体积=长×宽×高=底面积×高=横截面×长。
9.2.5米
【分析】根据长方体的体积公式V=Sh可知,长方体的高h=V÷S,代入数据计算,即可求出池内水的深度。
【详解】45÷18=2.5(米)
池内水深2.5米。
【点睛】本题考查长方体体积计算公式的灵活运用。
10.4/四
【分析】根据题意,用52厘米长的铁丝做一个高5厘米的长方体模型,那么铁丝的长度等于长方体的棱长总和,根据长方体的棱长总和=(长+宽+高)×4可知,长方体的长与宽之和=棱长总和÷4-高,判断哪两个整数相加等于长与宽的和,由此确定长与宽,进而得出能做成几种不同的长方体模型。
【详解】52÷4-5
=13-5
=8(厘米)
能做成的长方体分别是:
长7厘米,宽1厘米,高5厘米;
长6厘米,宽2厘米,高5厘米;
长5厘米,宽3厘米,高5厘米;
长4厘米,宽4厘米,高5厘米;
能做成4种不同的长方体。
【点睛】灵活运用长方体的棱长总和公式求出宽与高的和是解题的关键。
11. 62.5 25
【分析】根据正方体的总棱长=棱长×12,据此求出正方体的棱长;把这个正方体切成两个相同的长方体,这个长方体的长和高是正方体的棱长,宽是正方体棱长的一半,再根据长方体的体积公式:V=abh,据此进行计算即可;这个长方体最大的面是一个长方形,该长方形的长和宽都是正方体的棱长,据此解答即可。
【详解】60÷12=5(cm)
5×(5÷2)×5
=5×2.5×5
=12.5×5
=62.5(cm3)
5×5=25(cm2)
则把这个正方体切成两个相同的长方体,一个长方体的体积是62.5 SKIPIF 1 < 0 ,这个长方体最大一个面的面积25 SKIPIF 1 < 0 。
【点睛】本题考查长方体的体积,熟记公式是解题的关键。
12.56
【分析】将这块大理石的长和高的一面放在地上,此时占地面积最大,利用乘法求出此时的占地面积。
【详解】8×7=56(dm2)
所以,它的占地面积最大是56dm2。
【点睛】本题考查了长方体的底面积,长方体的底面是长方形,长方形的面积=长×宽。
13.48
【分析】相交于一个顶点的三条棱的长度分别是3分米、4分米、5分米,即长方体的长、宽、高,然后长方体的总棱长=(长+宽+高)×4,据此代入数值进行计算即可。
【详解】(3+4+5)×4
=12×4
=48(分米)
【点睛】本题考查长方体的总棱长,明确相交于一个顶点的三条棱就是长方体的长、宽和高是解题的关键。
14.192
【分析】根据长方体的平面展开图可知,长方体的长是12厘米,宽是4厘米,高是4厘米,根据长方体的体积公式:长×宽×高,代入数据,即可解答。
【详解】12×4×4
=48×4
=192(立方厘米)
【点睛】解答本题的关键是根据长方体的平面展开图确定长方体的长、宽、高的长度,再根据长方体体积公式进行解答。
15. 24 52
【分析】观察图形可知,长方体底面的长是6cm,宽是4cm,根据长方形的面积=长×宽,代入计算即可;求需要铁丝的长度,就是求长方体的棱长总和,根据长方体的棱长总和=(长+宽+高)×4,代入数据计算即可。
【详解】6×4=24(平方厘米),这个长方体的底面积是24平方厘米。
(6+4+3)×4
=13×4
=52(厘米)
至少需要52厘米的铁丝。
【点睛】此题考查了长方体的特征以及棱长总和的计算,找出长方体的长、宽、高是解题关键。
16. 大 相等
【分析】所有立体图形外面的面积之和叫做它的表面积;长方体切成两个相等的正方体面数增多,面积与原来相比会增加;体积是指物质或物体所占空间的大小;这两个正方体的体积之和与原来长方体所占空间大小不变;据此解答。
【详解】把一个长10厘米、宽和高都是5厘米的长方体切成两个相等的正方体。这两个正方体的表面积之和比原来长方体(大);这两个正方体的体积之和与原来长方体相比,(相等)。
【点睛】此题考查了立体图形的切拼,关键能够理解切开前后的面积与体积变化。
17.×
【分析】体积是指物质或物体所占空间的大小,一般从物体外表测量;容积是指容器所能容纳物体的体积,一般从物体的里面测量,体积不能完全等同容积;据此解答。
【详解】虽然单位:100立方分米=100升,但是体积是100立方分米的油箱,它的容积小于100升,实际物体的容积不能完全等同体积,还会有容器表皮的厚度,原题说法错误;
故答案为:×
【点睛】此题考查了体积与容积的区别,关键理解概念。
18.×
【分析】1米=10分米,棱长1米的正方体的体积是:10×10×10=1000(立方分米),棱长为1分米的正方体的体积是:1×1×1=1(立方分米 ),棱长1米的正方体可切成:1000÷1=1000(个),据此解答。
【详解】1米=10分米
10×10×10
=100×10
=1000(立方分米)
1×1×1=1(立方分米)
1000÷1=1000(个)
故原题说法错误。
【点睛】将棱长1米转化为棱长10分米,计算出大正方体的体积是解答本题的关键。
19.√
【分析】正方体的体积=棱长×棱长×棱长,再根据因数与积的变化规律,积扩大的倍数等于因数扩大倍数的乘积,据此判断。
【详解】正方体的棱长扩大2倍,正方体的体积扩大2×2×2=8倍。
故答案为:√
【点睛】此题主要考查正方体的体积公式的灵活运用,以及因数与积的变化规律的应用。
20.√
【详解】略
21.512cm3;40dm3
【分析】根据题意可知,把正方体的棱长的数据代入到正方体的体积公式:V=a×a×a,即可求出正方体的体积;把长方体的长、宽、高的数据代入长方体的体积公式:V=a×b×h,即可求出长方体的体积。
【详解】8×8×8=512(cm3)
2.5×2×8=40(dm3)
即图形1的体积是512cm3,图形2的体积是40dm3。
22.(1)20750dm3;(2)165dm3
【详解】(1)36×25×25﹣7×10×25
=900×25-70×25
=22500﹣1750
=20750(dm3)
(2)5.5×12×2+5.5×(12﹣4.5×2)×2
=5.5×12×2+5.5×(12﹣9)×2
=5.5×12×2+5.5×3×2
=66×2+16.5×2
=132+33
=165(dm3)
23.48立方厘米
【分析】根据长方体的棱长和公式:长方体棱长和=(长+宽+高)×4,设这个长方体的高是x厘米,长是3x厘米,宽是2x厘米,列方程为(x+3x+2x)×4=48,然后解出x的值,也就是高,进而求出长和宽,最后根据长方体的体积=长×宽×高求出这个长方体的体积。
【详解】解:设这个长方体的高是x厘米。
(x+3x+2x)×4=48
6x×4=48
24x=48
x=48÷24
x=2
2×3=6(厘米)
2×2=4(厘米)
2×6×4=48(立方厘米)
答:这个长方体的体积是48立方厘米。
【点睛】本题考查了长方体棱长和公式、体积公式的灵活应用,可用假设法解决问题。
24.11340块
【分析】根据长方体体积=长×宽×高,求出围墙体积,围墙体积×每立方米用砖数量=共用砖数量,据此列式解答。
【详解】24厘米=0.24米
30×0.24×3×525
=21.6×525
=11340(块)
答:这墙共用砖11340块。
【点睛】关键是掌握并灵活运用长方体体积公式。
25.装不下
【分析】先根据进率:1立方分米=1000立方厘米,将40立方分米换算成40000立方厘米;然后根据长方体的高=体积÷(长×宽),求出容纳盒的高;最后用烤箱的长、宽、高分别与容纳盒的长、宽、高相比较,得出结论。
【详解】40立方分米=40000立方厘米
容纳盒的高:
40000÷(50×40)
=40000÷2000
=20(厘米)
50>45,40>30,20<25。
答:装不下。
【点睛】灵活运用长方体的体积计算公式以及体积单位的换算是解题的关键。
26.435.2千克
【分析】先利用正方体的体积(容积)公式:V=a3,求出正方体油桶的容积,即是装在油桶里柴油的最大体积,统一单位后,用油桶能装柴油的体积乘1升柴油的重量,即可求出柴油的质量。
【详解】80×80×80=512000(立方厘米)
512000立方厘米=512立方分米=512升
512×0.85=435.2(千克)
答:这个油桶可以装435.2千克柴油。
【点睛】此题的解题关键是灵活运用正方体的体积(容积)公式以及单位之间的换算。
27.27立方分米
【分析】珊瑚的体积等于上升部分水的体积,根据长方体体积=长×宽×高即可求得。
【详解】9×6×0.5
=54×0.5
=27(立方分米)
答:这块珊瑚的体积是27立方分米。
【点睛】把不规则物体的体积转化为上升部分水的体积是解答题目的关键。
28.136000平方厘米
【分析】观察图可知环保袋的长是30厘米,宽10厘米,高38厘米,由于环保手提袋是没有盖的,根据长方体的表面积公式:S=ab+(ah+bh)×2,求出袋子的面积,再加上每个手提袋把手用布料的60立方厘米就是整个环保袋所用的布料,乘40就是做40个这样的手提环保袋所用的布料。
【详解】30×10+(30×38+10×38)×2+60
=300+(1140+380)×2+60
=3340+60
=3400(平方厘米)
3400×40=136000(平方厘米)
答:做40个这样的手提袋至少需要136000平方厘米的环保布料。
【点睛】此题主要考查长方体的表面积的计算。
29.14.4米
【分析】根据长方体的特征,长方体有12条棱,互相平行(相对)的一组4条棱的长度相等,求这个柜台需要多少米铝,就是求长方体的棱长总和,根据“长方体的棱长总和=(长+宽+高)×4”,据此代入数值进行计算即可。
【详解】60厘米=0.6米,
(2.2+0.6+0.8)×4
=3.6×4
=14.4(米)
答:这个柜台至少需要14.4米铝合金条。
【点睛】此题主要利用求长方体的棱长总和的方法解决实际问题,解答此题注意长度单位的换算。
30.400立方厘米
【分析】水面上升的体积就是5块石头的体积,用鱼缸底面积×水面上升的高度,求出5块石头的体积和,再除以5即可。
【详解】50×20×2÷5
=2000÷5
=400(立方厘米)
答:每块彩色石头的体积是400立方厘米。
【点睛】关键是利用转化思想,将求不规则物体的体积转化为求长方体等规则物体的体积。
小学数学青岛版(2024)五年级下册五 关注环境--分数加减法(二)课后练习题: 这是一份小学数学青岛版(2024)五年级下册<a href="/sx/tb_c122157_t7/?tag_id=28" target="_blank">五 关注环境--分数加减法(二)课后练习题</a>,共17页。试卷主要包含了选择题,填空题,判断题,计算题,解答题等内容,欢迎下载使用。
小学数学青岛版(2024)五年级下册四 走进军营——方向与位置课时作业: 这是一份小学数学青岛版(2024)五年级下册<a href="/sx/tb_c48095_t7/?tag_id=28" target="_blank">四 走进军营——方向与位置课时作业</a>,共16页。试卷主要包含了选择题,填空题,判断题,作图题,解答题等内容,欢迎下载使用。
数学青岛版(2024)三 剪纸中的数学--分数加减法(一)练习题: 这是一份数学青岛版(2024)<a href="/sx/tb_c122156_t7/?tag_id=28" target="_blank">三 剪纸中的数学--分数加减法(一)练习题</a>,共15页。试卷主要包含了选择题,填空题,判断题,计算题,解答题等内容,欢迎下载使用。














