北师大版（2024）九年级上册2 视图课时训练

这是一份北师大版（2024）九年级上册2 视图课时训练，共15页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

一、单选题
1．如图所示的几何体的左视图是（ ）`

A． B． C． D．
2．如图，六个大小相同的正方体拼成的几何体，其左视图为（ ）

A． B． C． D．
3．如图是由五个小正方体组合而成的一个立体图形，它的主视图是（ ）
A．B．C． D．
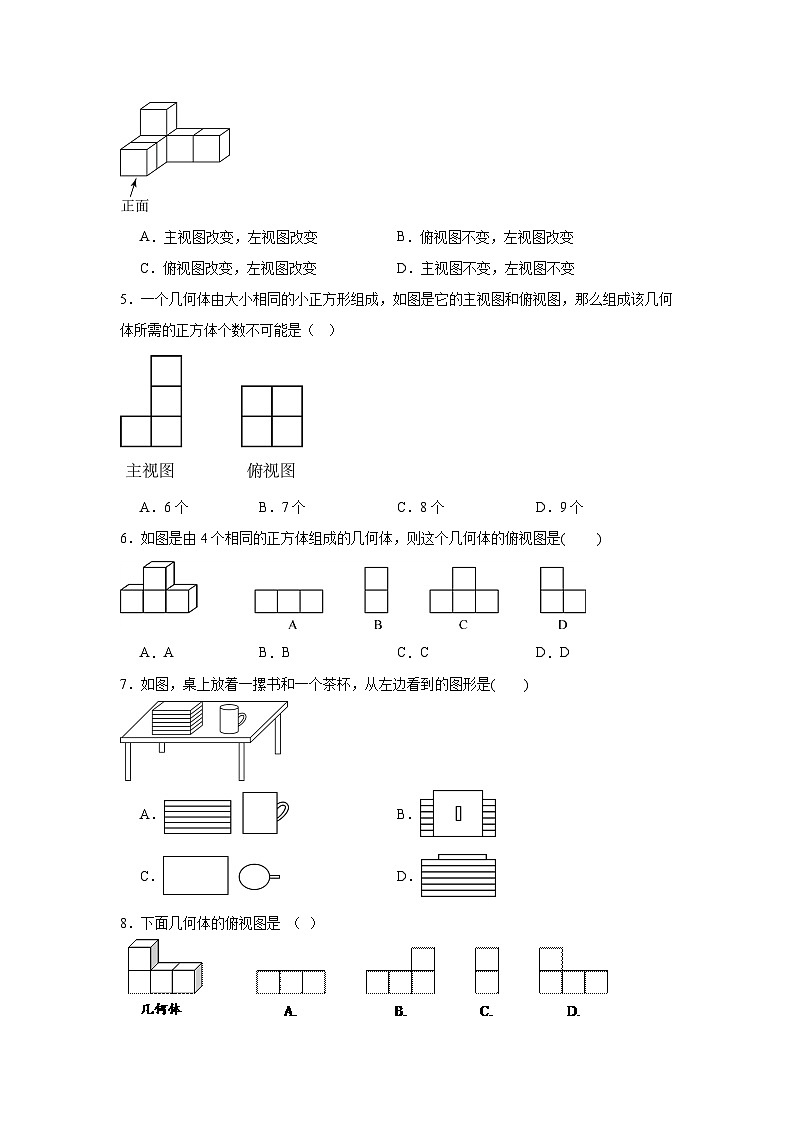
4．如图，将小立方块①从6个大小相同的小立方块所搭的几何体中移走后，所得几何体（ ）
A．主视图改变，左视图改变B．俯视图不变，左视图改变
C．俯视图改变，左视图改变D．主视图不变，左视图不变
5．一个几何体由大小相同的小正方形组成，如图是它的主视图和俯视图，那么组成该几何体所需的正方体个数不可能是（ ）

A．6个B．7个C．8个D．9个
6．如图是由4个相同的正方体组成的几何体，则这个几何体的俯视图是( )
A．AB．BC．CD．D
7．如图，桌上放着一摞书和一个茶杯，从左边看到的图形是( )
A．B．
C．D．
8．下面几何体的俯视图是 （ ）

A．AB．BC．CD．D
9．如图是一个几何体的三视图，这个几何体是（ ）
A．B．C．D．
10．如图所示，从上面看该几何体的形状图为（ ）

A． B．
C． D．
11．将一个正方体沿正面相邻两条棱的中点连线截去一个三棱柱，得到一个如图所示的几何体，则该几何体的左视图是( )
A．B．C．D．
12．榫卯是中国传统建筑、家具及其他器械的主要结构方式，是我国工艺文化精神的传承，凸出部分叫榫，凹进部分叫卯．某个部件“卯”的实物图如图所示，它的俯视图是（ ）
A．B．
C．D．
二、填空题
13．某长方体的主视图和俯视图如图所示，则该长方体的左视图的面积是 ．
14．一个几何体由若干大小相同的小立方块搭成，如图分别是从它的正面、上面看到的形状图，则该几何体至少是用 个小立方块搭成的．
15．一个几何体是由一些完全相同的小立方块搭成的，从正面和上面看到的图形如图所示，则搭成这个几何体最多需这样的小方块 个．
16．如图，是某一个几何体的俯视图，主视图、左视图，则这个几何体是 ．

17．如图所给的三视图表示的几何体是 ．
三、解答题
18．空间任意选定一点，以点为端点作三条互相垂直的射线，，．这三条互相垂直的射线分别称作轴、轴、轴，统称为坐标轴，它们的方向分别为（水平向前），（水平向右），（竖直向上）方向，这样的坐标系称为空间直角坐标系．将相邻三个面的面积记为，且的小长方体称为单位长方体，现将若干个单位长方体在空间直角坐标系内进行码放，要求码放时将单位长方体所在的面与轴垂直，所在的面与轴垂直，所在的面与轴垂直，如图所示．若将轴方向表示的量称为几何体码放的排数，轴方向表示的量称为几何体码放的列数，轴方向表示的量称为几何体码放的层数；如图是由若干个单位长方体在空间直角坐标内码放的一个几何体，其中这个几何体共码放了排列层，用有序数组记作 (1，2，6)，如图的几何体码放了排列层，用有序数组记作 (2，3，4)．这样我们就可用每一个有序数组表示一种几何体的码放方式．
（1）有序数组 (3，2，4)所对应的码放的几何体是_____；
（2）图是由若干个单位长方体码放的一个几何体的三视图，则这种码放方式的有序数组为(___，____，____)，组成这个几何体的单位长方体的个数为____个；
（3）为了进一步探究有序数组的几何体的表面积公式，某同学针对若干个单位长方体进行码放，制作了下列表格：
根据以上规律，请直接写出有序数组的几何体表面积的计算公式；（用表示）
（4）当时，对由个单位长方体码放的几何体进行打包，为了节约外包装材料，我们可以对个单位长方体码放的几何体表面积最小的规律进行探究，请你根据自己探究的结果直接写出使几何体表面积最小的有序数组，这个有序数组为(___，___，___)，此时求出的这个几何体表面积的大小为________．（缝隙不计）
19．如图，是一个几何体从三个方向看所得到的形状图．
（1）写出这个几何体的名称；
（2）画出它的一种表面展开图；
（3）若从正面看长方形的高为，从上面看三角形的边长都为，求这个几何体的侧面积．
20．如图是由若干个小正方体木块搭建成的几何体从正面，左面和上面看到的形状图，请在从上面看到的形状图中标出相应位置上小立方体木块的个数．
21．第24届冬奥会吉祥物“冰墩墩”收获无数“迷弟”“迷妹”而一“墩”难求；为了满足需求，其中一间正规授权生产厂通过技术改造来提高产能，两次技术改造后，由日产量2000个扩大到日产量2420个．
(1)求这两次技术改造日产量的平均增长率；
(2)这生产厂家还设计了三视图如图所示的“冰墩墩”盲盒，（单位：），请计算此类盲盒的表面积．
22．如图是由10个棱长为的小正方体搭成的几何体．
(1)请在方格图中分别画出该物体的主视图和俯视图；
(2)若将这个几何体外表面涂上一层漆（包括底面），则其涂漆面积为______；
(3)在不改变主视图和俯视图的情况下，最多还可以添加______个小正方体．
参考答案：
1．A
【分析】根据从左边看得到的图形是左视图，可得答案．
【详解】解：从左边看是一个两个同心圆，
故选：A．
【点睛】本题考查三视图，解题的关键是理解三视图、看懂三视图，属于中考常考题型．
2．D
【分析】根据从左边看得到的图形是左视图，可得答案；
【详解】
由题意知，题中几何体的左视图为
故选：D
【点睛】本题主要考查三视图的知识，熟练掌握三视图的方法是解题的关键
3．B
【分析】找出几何体从正面看所得到的图形即可．
【详解】解：从正面看，第一行有三个小立方体，第二行有一个小立方体；
如图：
故选：B.
【点睛】此题主要考查了简单几何体的三视图，关键是掌握所看的位置．
错因分析：容易题.选错的原因是三视图的判断方法未掌握.
4．C
【分析】主视图是从立体图形的正面看，俯视图是从立体图形的上面看，左视图是从立体图形的左面看，根据题意，只需要考虑小立方块移走前后三视图的变化，即可做出选择．
【详解】主视图是从立体图形的正面看，俯视图是从立体图形的上面看，左视图是从立体图形的左面看，故将小立方块移走后，主视图不变，左视图和俯视图均发生改变．
故选择C．
【点睛】本题主要考查三视图，判断小立方块移走前后的变化是解决本题的关键．
5．D
【分析】根据三视图的知识，易得这个几何体共有三层，两行，两列，先看右边一列可能的最多和最少个数，在看左边一列可能的最多和最少个数，相加即可．
【详解】解：综合俯视图和主视图，这个几何体的右边一列最少4个正方体，最多6个正方体，左边一列只能有2个正方体，则总各数可能是6个或7个或8个，
故选：D．
【点睛】本题考查由三视图判断几何体，学生对三视图掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考查．如果掌握口诀“俯视图打地基，正视图疯狂盖，左视图拆违章”就容易得到答案．
6．A
【详解】根据三视图中俯视图的定义,从物体上面看所得到的图形,是三个小正方形组成的长方形,故选A.
点睛:本题主要三视图的定义,解决本题的关键是要熟练掌握俯视图的定义.
7．D
【详解】试题解析：从左面可看到几个上下相邻的长方形上面有一个小长方形．
故选D．
8．A
【详解】分析：找到从上面看所得到的图形即可,注意所有看得到的棱都应表现在俯视图中.详解：从上面看,这个几何体只有一层,且有3个小正方形,故选A.
点睛：本题考查了三视图的知识,俯视图是从物体的上面看得到的视图.
9．A
【分析】结合三视图确定各图形的位置后进行逆向想象即可确定正确的选项．
【详解】解：从主视图与左视图是长方形，该几何体是柱体，
从俯视图看到的图形是三角形，该几何体是三棱柱，
结合三个视图发现，这个几何体是直三棱柱．
故选：A．
【点睛】本题考查了由三视图判断几何体的知识，解题的关键是能够正确的确定各个图形的位置，难度不大．
10．C
【分析】俯视图是从物体上面所看到的图形，可根据物体的特点作答；
【详解】解：这是一个中间部分掏空的长方体，根据俯视图是从物体上面所看到的图形，
故选：C
【点睛】本题考查了三视图的知识，俯视图是从物体的上面看得到的视图，根据物体的特征回答是解题的关键．
11．B
【分析】根据左视图的定义画出左视图即可得答案.
【详解】从左面看，是正方形，对面中间有一条看不见的棱，用虚线表示，
∴B选项符合题意，
故选B.
【点睛】此题主要考查了简单几何体的三视图，左视图是从左面看所得到的图形．
12．A
【分析】本题主要考查了简单组合体的三视图，掌握组合体的三视图是解题的关键．
根据从上面看得到的图形是俯视图，可得答案．
【详解】解：从上面看，是一个矩形，矩形的中间有2条纵向的实线和2条纵向的虚线．2条实线在2条虚线之间，即
故选：A．
13．3
【分析】本题考查简单几何体的三视图，根据主视图和俯视图求出左视图长为3，宽为1，即可求解．
【详解】由图可知，该长方体长、宽、高为4、3、1，
故左视图长为3，宽为1， 故面积为
故答案为：3．
14．6
【分析】根据题意可以得到该几何体从正面和上面看至少有多少个小立方体，综合考虑即可解答本题．
【详解】解：从正面看至少有三个小立方体且有两层；从上面看至少有五个小立方体，且有两列；
∴只需要保证从正面看的上面一层有一个，从上面看有五个小立方体即可满足题意，
∴最少是用6个小立方块搭成的，
故答案为：6．
【点睛】此题主要考查学生对三视图掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考查．如果掌握口诀“俯视图打地基，正视图疯狂盖，左视图拆违章”就更容易得到答案．
15．10
【分析】从俯视图中可以看出最底层小正方体的个数及形状，从主视图可以看出每一层小正方体的层数和个数，从而算出总的个数．
【详解】解：综合主视图和俯视图，
可知底层可有6个正方体，第二层可有2个正方体，第三层可有2个正方体，
所以搭成这个几何体最多需小立方块10个．
故答案为：10．
【点睛】本题主要考查从不同方向看几何体，熟练掌握几何体的特征是解题的关键．
16．圆柱
【详解】解：这个几何体是圆柱．故答案为圆柱．
17．圆锥
【分析】本题考查了简单几何体的三视图，根据简单几何体三视图的特征即可解答．
【详解】解：由主视图和左视图都是等腰三角形，俯视图是有圆心的圆可得该几何体是圆锥．
故答案为：圆锥 ．
18．（1）B；（2）；；；；（3）；（4）；；；．
【分析】（1）根据有序数组中x、y和z表示的实际意义即可得出结论；
（2）根据三视图的定义和有序数组中x、y和z表示的实际意义即可得出结论；
（3）根据题意，分别从不同方向找出面积为、和的长方形，用含x、y、z的式子表示出它们的个数，然后根据表面积公式计算即可；
（4）由题意可知：xyz=12，而12=1×1×12=1×2×6=1×3×4=2×2×3，然后分类讨论，根据（3）的公式分别求出在每一种情况下的最小值，最后通过比较找出最小的即可得出结论．
【详解】解：（1）有序数组 (3，2，4)表示3排2列4层，故B选项符合
故选：B．
（2）由左视图和俯视图可知：该几何体共码放了2排，由主视图和俯视图可知：该几何体共码放了3列，由主视图和左视图可知：该几何体共码放了2层，
故这种码放方式的有序数组为（，，）；
组成这个几何体的单位长方体的个数为2×3×2=；
故答案为：；；；；
（3）根据题意可知：从几何体的前面和后面看：面积为的长方形共有2yz个，从几何体的左面和右面看：面积为的长方形共有2xz个，从几何体的上面和下面看：面积为的长方形共有2xy个，
∴几何体表面积
（4）由题意可知：xyz=12，而12=1×1×12=1×2×6=1×3×4=2×2×3
①当xyz= 1×1×12时
∵
根据（3）中公式可知，此时当x=1，y=1，z=12时，几何体表面积最小
此时；
②当xyz= 1×2×6时
∵
根据（3）中公式可知，此时当x=1，y=2，z=6时，几何体表面积最小
此时；
③当xyz=1×3×4时
∵
根据（3）中公式可知，此时当x=1，y=3，z=4时，几何体表面积最小
此时；
④当xyz=2×2×3时
∵
根据（3）中公式可知，此时当x=2，y=2，z=3时，几何体表面积最小
此时；
∵
∴这个有序数组为（，，），最小面积为．
故答案为：；；；92．
【点睛】此题考查的是新定义类问题，读懂材料、并归纳总结公式和掌握三视图的概念和表面积的求法和分类讨论的数学思想是解决此题的关键．
19．（1）正三棱柱；（2）详见解析；（3）135cm2．
【分析】（1）根据几何体的三视图，可知，几何体是正三棱柱；
（2）根据几何体的侧面展开图的定义，即可得到答案；
（3）根据正三棱柱的侧面是长方形，进而即可求出侧面积．
【详解】（1）∵三棱柱的侧面是长方形，底面是等边三角形，
∴几何体是正三棱柱；
（2）表面展开图如下；
（3）S侧=3×5×9=3×45=135(cm2)；
答：这个几何体的侧面积是135cm2．
【点睛】本题主要考查正三棱柱的三视图，表面展开图以及侧面积，掌握几何体的三视图的定义和表面展开图的定义，是解题的关键．
20．答案见解析
【分析】本题考查了三视图，由三视图判断几何体的知识，熟练掌握三视图是解题的关键．
由俯视图可得该组合几何体最底层的小木块的个数，由主视图和左视图可得第二层和第三层小木块的个数，依此将得到的正方体的个数在俯视图上标出来即可．
【详解】解：俯视图中有5个正方形，
最底层有5个正方体小木块，
由主视图和左视图可得第二层有2个正方体小木块，第三层有1个正方体小木块，
如图所示：
21．(1)10%
(2)
【分析】（1）设这两次技术改造日产量的平均增长率为x，然后根据两次技术改造后，由日产量2000个扩大到日产量2420个，列出方程求解即可；
（2）由三视图可知，这个盲盒为圆柱纵切的一半，其中底面圆半径为4cm，高为8cm，由此求解即可．
【详解】（1）解：设这两次技术改造日产量的平均增长率为x，
由题意得：，
解得（负值已经舍去），
答：这两次技术改造日产量的平均增长率为10%；
（2）解：由三视图可知，这个盲盒为圆柱纵切的一半，其中底面圆半径为4cm，高为8cm，
∴
【点睛】本题主要考查了一元二次方程的应用，根据三视图求几何体的表面积等等，熟知相关知识是解题的关键．
22．(1)见解析
(2)38
(3)3
【分析】本题考查了三视图，解题关键是理解三视图的定义，灵活运用所学知识解决问题．
（1）根据几何体分别画出图形即可；
（2）分别通过三视图，计算涂漆面积即可；
（3）根据主视图和俯视图分析可添加的正方体数量即可．
【详解】（1）解：主视图和俯视图如图，
（2）解：由视图计算涂漆面积为
，
故答案为：38；
（3）解：根据主视图和俯视图可知，在不改变主视图和俯视图的情况下，添加小正方体如图，
故可增加3个小正方体，
故答案为：3．
题号
1
2
3
4
5
6
7
8
9
10
答案
A
D
B
C
D
A
D
A
A
C
题号
11
12








答案
B
A