鲁教版（五四学制）（2024）九年级下册3 垂径定理复习练习题

这是一份鲁教版（五四学制）（2024）九年级下册3 垂径定理复习练习题，共13页。试卷主要包含了如图，P是⊙O内一点等内容，欢迎下载使用。
一．选择题（共6小题）
1．如图，AB为⊙O的直径，弦CD⊥AB于点E，已知CD＝8，EB＝2，则⊙O的半径为（ ）
A．5B．4C．8D．6
2．如图，AB是⊙O的直径，弦CD⊥AB，垂足为点P，若AP＝2，PB＝8，则弦CD的长是（ ）
A．10B．8C．5D．3
3．如图，AB是⊙O的直径，BC是弦，OD∥AC交于点D，交BC于点E，若BC＝8，ED＝2，则⊙O的半径是（ ）
A．3B．4C．5D．2
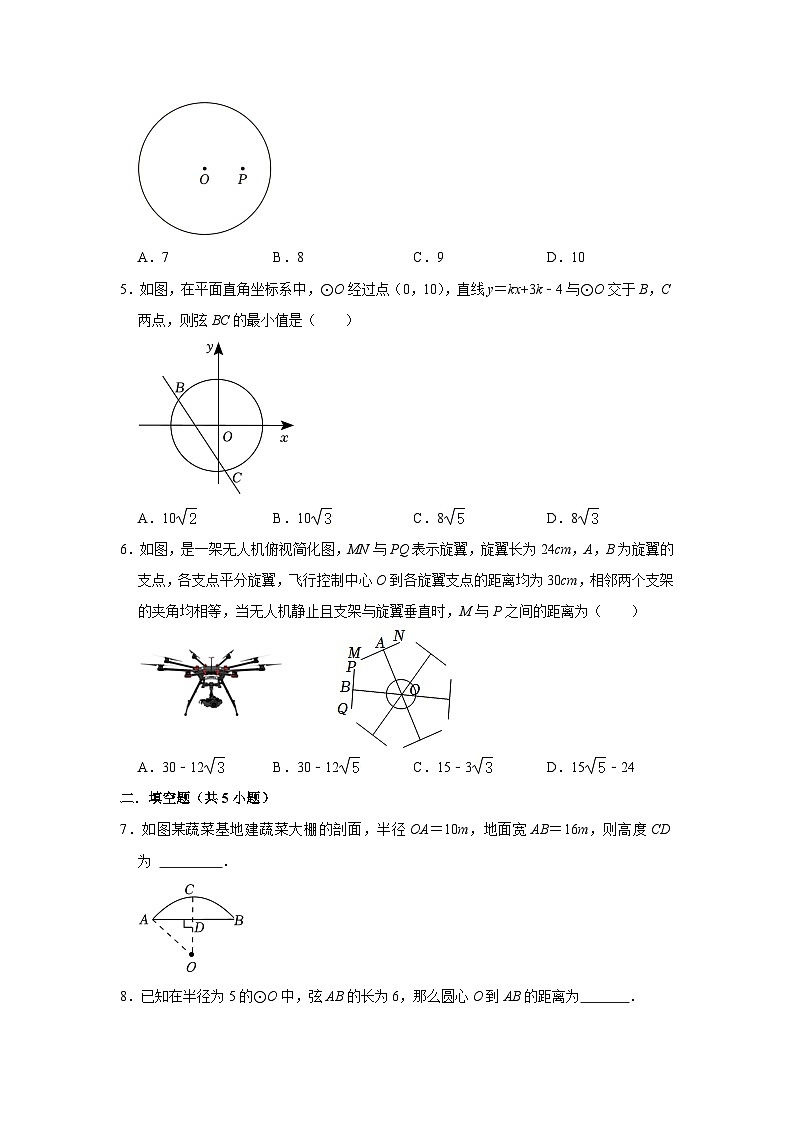
4．如图，P是⊙O内一点．若圆的半径为5，OP＝3，则经过点P的弦的长度不可能为（ ）
A．7B．8C．9D．10
5．如图，在平面直角坐标系中，⊙O经过点（0，10），直线y＝kx+3k﹣4与⊙O交于B，C两点，则弦BC的最小值是（ ）
A．10B．10C．8D．8
6．如图，是一架无人机俯视简化图，MN与PQ表示旋翼，旋翼长为24cm，A，B为旋翼的支点，各支点平分旋翼，飞行控制中心O到各旋翼支点的距离均为30cm，相邻两个支架的夹角均相等，当无人机静止且支架与旋翼垂直时，M与P之间的距离为（ ）
A．30﹣12B．30﹣12C．15﹣3D．15﹣24
二．填空题（共5小题）
7．如图某蔬菜基地建蔬菜大棚的剖面，半径OA＝10m，地面宽AB＝16m，则高度CD为 ．
8．已知在半径为5的⊙O中，弦AB的长为6，那么圆心O到AB的距离为 ．
9．现在很多家庭都使用折叠型餐桌来节省空间，两边翻开后成为圆形桌面（如图①），餐桌两边AD和BC平行且相等，AB⊥AD（如图②），小华用皮尺量得AC＝1.6米，AB＝0.8米，那么桌面翻成圆桌后，桌子面积会增加 平方米．
10．一条排水管横截面如图所示，已知排水管半径OA＝1m，水面宽CD＝1.6m，若管内水面下降0.2m，则此时水面宽AB等于 m．
11．如图1，筒车是我国最古老的农业水利灌溉工具，是珍贵的历史文化遗产．如图2，筒车盛水桶的运行轨道是以轴心O为圆心的圆，圆心O在水面上方，且⊙O被水面截得的弦AB长为3米，半径为2米，则圆心O到水面AB的距离为 米．
三．解答题（共4小题）
12．如图，AB为半圆O中的直径，CD⊥AB于D，求证：CD2＝AD•BD．
13．如图，在⊙O中，AB，BC为互相垂直且相等的两条弦，OD⊥AB，OE⊥BC，垂足分别为D，E，求证：四边形ODBE是正方形．
14．如图，CD为⊙O的直径，CD⊥AB，垂足为F，AO⊥BC，垂足为E，BC＝2．
（1）求AB的长；
（2）求⊙O的半径．
15．如图，有一座拱桥是圆弧形，它的跨度AB＝60米，拱高PD＝18米．
（1）求圆弧所在的圆的半径r的长；
（2）当洪水泛滥到跨度只有30米时，要采取紧急措施，若拱顶离水面只有4米，即PE＝4米时，是否要采取紧急措施？
鲁教版九年级下册5.3垂径定理同步练习
参考答案与试题解析
一．选择题（共6小题）
1．【分析】连接OC，设⊙O的半径为R，根据垂径定理求出CE，根据勾股定理列式计算，得到答案．
【解答】解：连接OC，
设⊙O的半径为R，则OE＝R﹣2，
∵CD⊥AB，AB为⊙O的直径，
∴CE＝CD＝4，
由勾股定理得，OC2＝OE2+CE2，
即R2＝（R﹣2）2+42，
解得，R＝5，
则⊙O的半径为5，
故选：A．
2．【分析】连接OC，根据AB是⊙O的直径，AP＝2，PB＝8得出⊙O的半径，故可得出OP的长，再由弦CD⊥AB可知PC＝CD，根据勾股定理求出PC的长，进而可得出结论．
【解答】解：连接OC，
∵AB是⊙O的直径，AP＝2，PB＝8，
∴⊙O的半径＝（2+8）＝5，
∴OP＝PB﹣OB＝8﹣5＝3，
∵弦CD⊥AB，
∴PC＝CD，∠CPO＝90°，
∴PC＝＝＝4，
∴CD＝2PC＝8．
故选：B．
3．【分析】由圆周角定理得∠ACB＝90°，再证OD⊥BC，由垂径定理得BE＝BC＝4，设⊙O的半径为r，则OE＝r﹣2，然后在Rt△OBE中，由勾股定理得出方程，解方程即可．
【解答】解：∵AB是⊙O的直径，
∴∠ACB＝90°，
∵OD∥AC，
∴∠OEB＝∠ACB＝90°，
∴OD⊥BC，
∴BE＝BC＝4，
设⊙O的半径为r，则OE＝r﹣2，
在Rt△OBE中，由勾股定理得：42+（r﹣2）2＝r2，
解得：r＝5，
即⊙O的半径为5，
故选：C．
4．【分析】连接OP，过P作弦AB⊥OP，此时AB是过P的最短的弦，由垂径定理得到AB＝2AP，由勾股定理求出AP＝＝4，得到AB＝8，过P的最长的弦是圆的直径是10，于是得到经过点P的弦长的取值范围，即可得到答案．
【解答】解：连接OP，过P作弦AB⊥OP，此时AB是过P的最短的弦，
∴AB＝2AP，
∵圆的半径为5，OP＝3，
∴AP＝＝＝4，
∴AB＝8，
∵过P的最长的弦是圆的直径是10，
∴8≤经过点P的弦的长≤10，
∴经过点P的弦的长度不可能是7．
故选：A．
5．【分析】根据直线y＝kx+3k﹣4的特点可知该直线过定点D（﹣3，﹣4），运用勾股定理可求出OD，⊙O经过点（0，10），可求出半径OB，由于过圆内定点D的所有弦中，与OD垂直的弦最短．
【解答】解：对于直线y＝kx+3k﹣4＝k（x+3）﹣4，
当x＝﹣3时，y＝﹣4，故直线恒经过点（﹣3，﹣4），记为点D．
由于过圆内定点D的所有弦中，与OD垂直的弦最短，即当OD⊥BC时，BC最短，
连接OB，如图所示
∵D（﹣3，﹣4）
∴，
∵⊙O经过点（0，10），
∴OB＝10，
∴．
∴．
故选：B．
6．【分析】如图，延长BP交AM的延长线于点J，连接OP，OM，OJ，OJ交PM于点K．首先求出PJ＝MJ＝（10﹣12）cm，再求出PK，可得结论．
【解答】解：如图，延长BP交AM的延长线于点J，连接OP，OM，OJ，OJ交PM于点K．
∵OJ＝OJ，OA＝OB，∠OAJ＝∠OBJ，
∴Rt△OAJ≌Rt△OBJ（HL），
∴JB＝JA，∠JOA＝∠JOB＝∠AOB＝30°，
∵OA＝30cm，
∴AJ＝BJ＝OB•tan30°＝10（cm），
∵PB＝AM＝12cm，
∴PJ＝JM＝（10﹣12）cm，
∵OJ⊥PM，
∴PK＝KM＝PJ•cs30°＝（10﹣12）×＝（15﹣6）cm，
∴PM＝2PK＝（30﹣12）cm．
故选：A．
二．填空题（共5小题）
7．【分析】根据图可知OC⊥AB，由垂径定理可知∠ADO＝90°，AD＝AB＝8m，在Rt△AOD中，利用勾股定理可求OD，进而可求CD．
【解答】解：∵OC⊥AB，
∴∠ADO＝90°，AD＝AB＝8（m），
在Rt△AOD中，OD2＝OA2﹣AD2，
∴OD＝＝6（m），
∴CD＝10﹣6＝4（m）．
故答案是：4m．
8．【分析】作OC⊥AB于C，连接OA，根据垂径定理得到AC＝BC＝AB＝3，然后在Rt△AOC中利用勾股定理计算OC即可．
【解答】解：作OC⊥AB于C，连接OA，如图，
∵OC⊥AB，
∴AC＝BC＝AB＝×6＝3，
在Rt△AOC中，OA＝5，
∴OC＝＝4，
即圆心O到AB的距离为4．
故答案为：4
9．【分析】首先将圆形补全，设圆心为O，连接DO，过点O作OE⊥AD于点E，进而得出AD，EO的长以及∠CAD，∠AOD的度数，进而得出S弓形AD＝S扇形AOD﹣S△AOD求出即可．
【解答】解：将圆形补全，设圆心为O，连接DO，过点O作OE⊥AD于点E，
由题意可得出：∠DAB＝∠ABC＝90°，
∴AC是⊙O的直径，
∵AC＝1.6米，AB＝0.8米，
∴∠ACB＝30°，
∵餐桌两边AB和CD平行且相等，
∴∠ACB＝∠DAC＝30°，
∴EO＝AO＝0.4（米），
∴AE＝＝，
∴AD＝2AE＝，
∵∠CAD＝∠D＝30°，
∴∠AOD＝120°，
∴S弓形AD＝S扇形AOD﹣S△AOD
＝，
＝﹣，
∴桌面翻成圆桌后，桌子面积会增加（﹣）平方米．
故答案为：（﹣）．
10．【分析】先根据勾股定理求出OE的长，再根据垂径定理求出CF的长，即可得出结论．
【解答】解：如图：连接OC，过O作OE⊥AB于E，交CD于F，
∵CD＝1.6m，OE⊥CD，OC＝OA＝1m，
∴CF＝0.8m，
∴OF＝＝0.6（m），
∵管内水面下降0.2m，
∴OE＝0.6+0.2＝0.8m，
∴AE＝＝＝0.6m，
∴AB＝1.2m．
故答案为：1.2．
11．【分析】过点O作OC⊥AB，连接OA，则AC＝AB＝1.5米，在Rt△AOC中用勾股定理可求OC．
【解答】解：过点O作OC⊥AB，连接OA，则AC＝AB＝1.5米，如图，
在Rt△AOC中，OC2＝OA2+AC2，
∴OC＝＝米．
故答案为：．
三．解答题（共4小题）
12．【分析】连接AC，BC，由垂直的定义得到∠CDB＝∠ADC＝90°，根据圆周角定理及余角的性质得到∠B＝∠ACD，证明△CDB∽△ADC，根据相似三角形的性质即可得到答案．
【解答】解：连接AC，BC，
∵CD⊥AB，
∴∠CDB＝∠ADC＝90°．
又AB是⊙O的直径，
∴∠ACB＝90°，∠A+∠B＝90°，∠A+∠ACD＝90°，
∴∠B＝∠ACD，
∴△CDB∽△ADC，
∴，
∴CD2＝AD⋅BD．
13．【分析】先根据垂径定理，由OD⊥AB，OE⊥AC得到AD＝AB，BE＝BC，且∠BDO＝∠B＝∠OEB＝90°，加上∠DAE＝90°，则可判断四边形ODBE是矩形，由于AB＝AC，所以BD＝BE，于是可判断四边形ADOE是正方形．
【解答】证明：∵OD⊥AB于D，OE⊥AC于E，AB⊥BC，
∴BD＝AB，BE＝BC，∠BDO＝∠B＝∠OEB＝90°，
∴四边形ODBE是矩形，
∵AB＝BC，
∴BD＝BE，
∴四边形ODBE是正方形．
14．【分析】（1）连接AC，根据垂径定理求出BE＝CE，AF＝BF，根据线段垂直平分线性质求出AC＝BC，AB＝AC，求出AB＝BC即可；
（2）求出∠BCD＝30°和CE＝，解直角三角形求出即可．
【解答】解：（1）如图连接AC，
∵AO⊥BC，AO过O，
∴CE＝BE，
∴AB＝AC，
同理AC＝BC，
∴AB＝BC＝2；
（2）∵AB＝BC＝AC，
∴△ABC是等边三角形，
∴∠ACB＝60°，
∵AC＝BC，CD⊥AB，
∴∠BCD＝30°，
在Rt△CEO中，OC＝＝2，
即⊙O的半径为2．
15．【分析】（1）连接OA，利用r表示出OD的长，在Rt△AOD中根据勾股定理求出r的值即可；
（2）连接OA′，在Rt△A′EO中，由勾股定理得出A′E的长，进而可得出A′B′的长，据此可得出结论．
【解答】解：（1）连接OA，
由题意得：AD＝AB＝30（米），OD＝（r﹣18）米，
在Rt△ADO中，由勾股定理得：r2＝302+（r﹣18）2，
解得，r＝34（米）；
（2）连接OA′，
∵OE＝OP﹣PE＝30米，
∴在Rt△A′EO中，由勾股定理得：A′E2＝A′O2﹣OE2，即：A′E2＝342﹣302，
解得：A′E＝16（米）．
∴A′B′＝32（米）．
∵A′B′＝32＞30，
∴不需要采取紧急措施．