初中人教版（2024）5.3.1 平行线的性质当堂达标检测题

这是一份初中人教版（2024）5.3.1 平行线的性质当堂达标检测题，共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
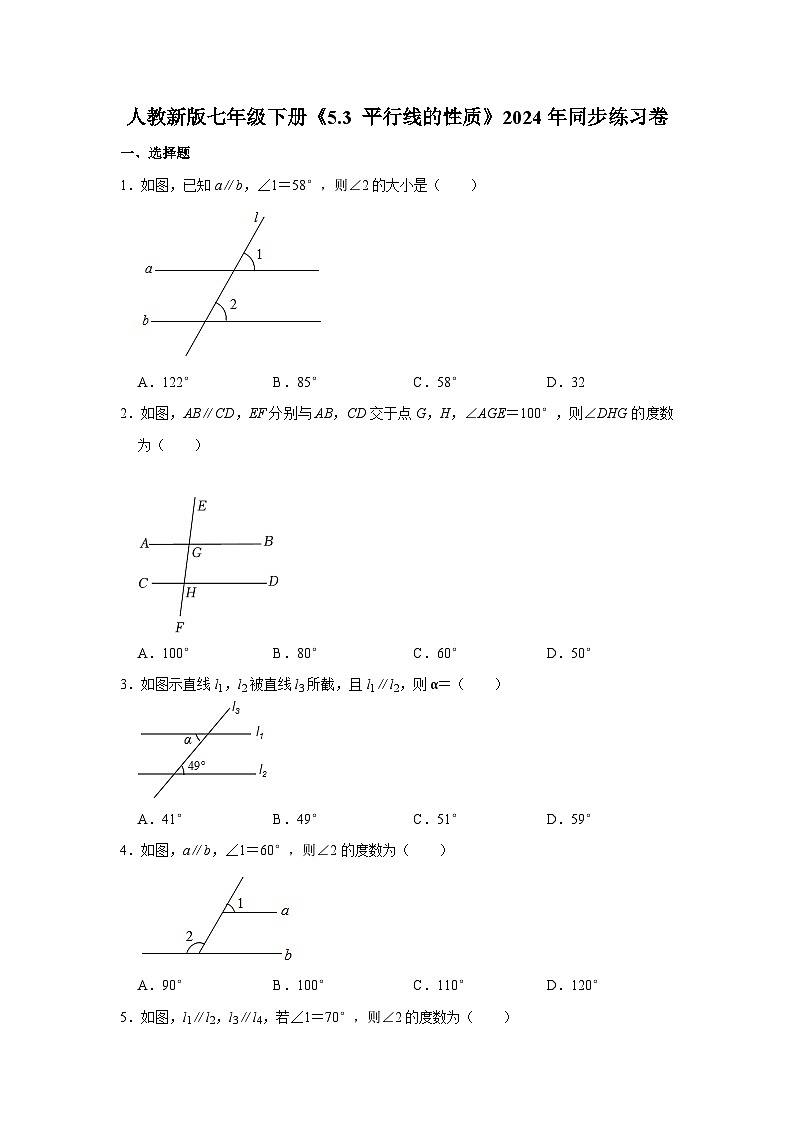
1．如图，已知a∥b，∠1＝58°，则∠2的大小是（ ）
A．122°B．85°C．58°D．32
2．如图，AB∥CD，EF分别与AB，CD交于点G，H，∠AGE＝100°，则∠DHG的度数为（ ）
A．100°B．80°C．60°D．50°
3．如图示直线l1，l2被直线l3所截，且l1∥l2，则α＝（ ）
A．41°B．49°C．51°D．59°
4．如图，a∥b，∠1＝60°，则∠2的度数为（ ）
A．90°B．100°C．110°D．120°
5．如图，l1∥l2，l3∥l4，若∠1＝70°，则∠2的度数为（ ）
A．100°B．110°C．120°D．130°
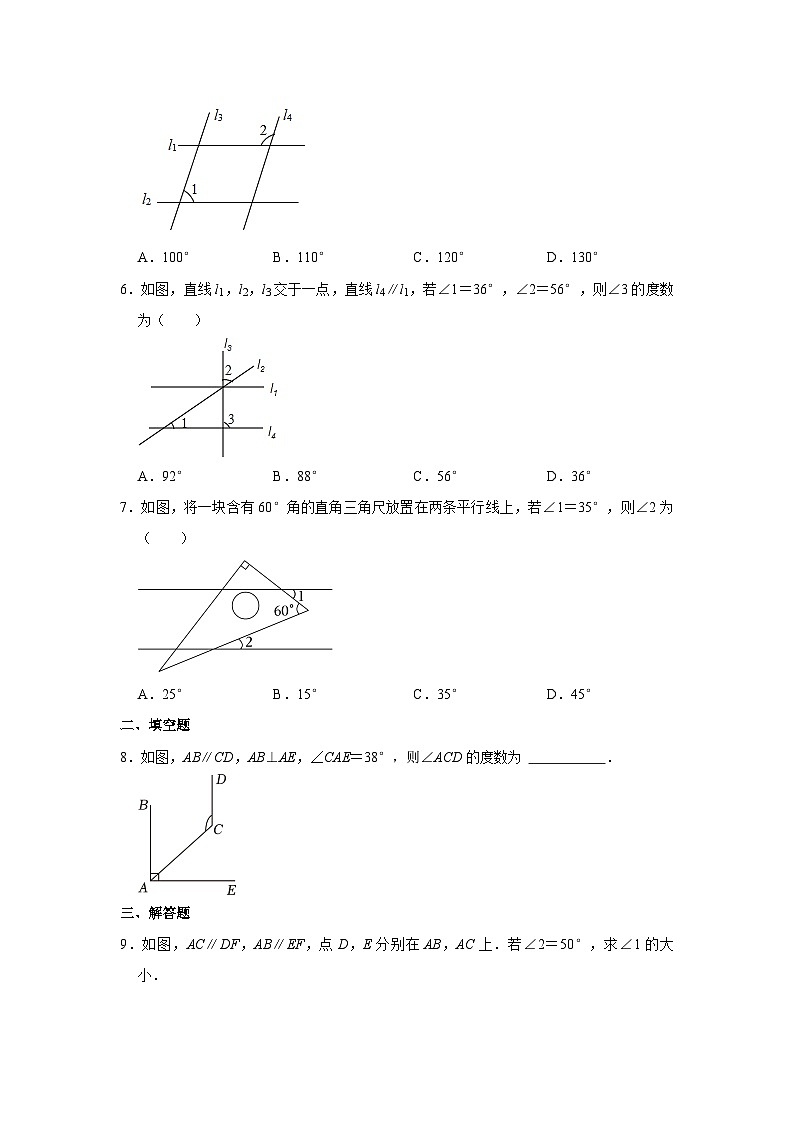
6．如图，直线l1，l2，l3交于一点，直线l4∥l1，若∠1＝36°，∠2＝56°，则∠3的度数为（ ）
A．92°B．88°C．56°D．36°
7．如图，将一块含有60°角的直角三角尺放置在两条平行线上，若∠1＝35°，则∠2为（ ）
A．25°B．15°C．35°D．45°
二、填空题
8．如图，AB∥CD，AB⊥AE，∠CAE＝38°，则∠ACD的度数为 ．
三、解答题
9．如图，AC∥DF，AB∥EF，点D，E分别在AB，AC上．若∠2＝50°，求∠1的大小．
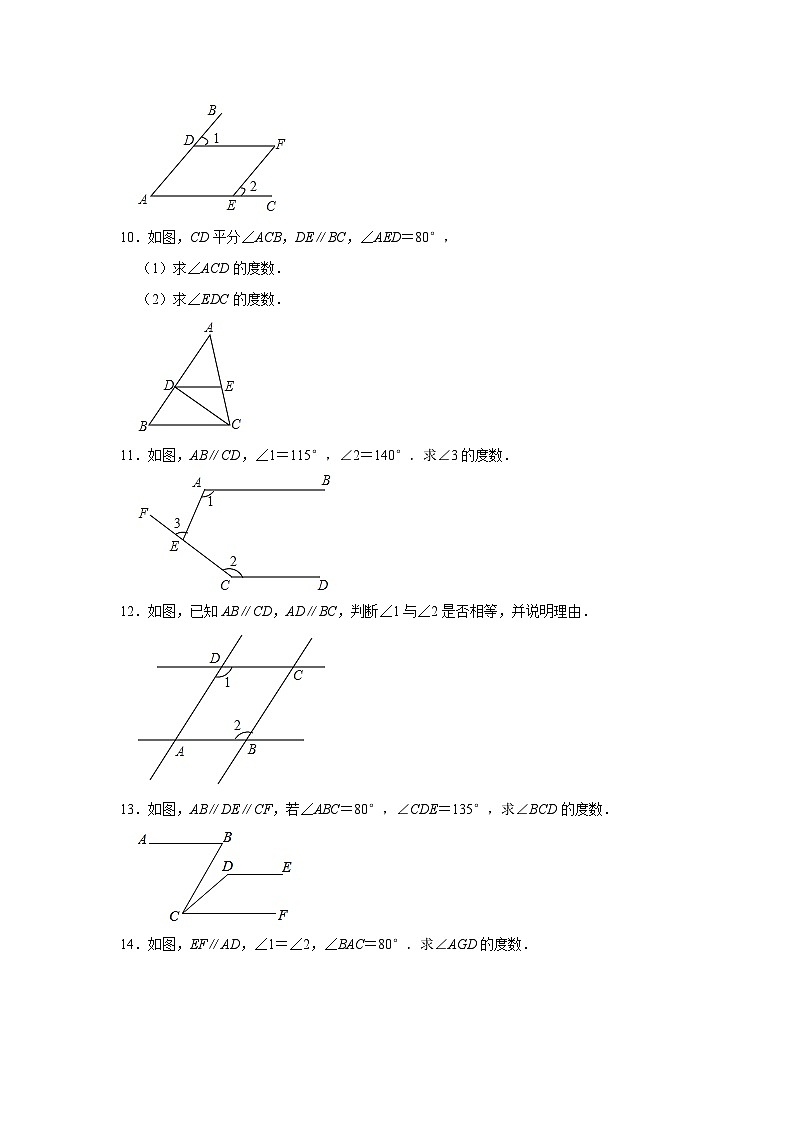
10．如图，CD平分∠ACB，DE∥BC，∠AED＝80°，
（1）求∠ACD的度数．
（2）求∠EDC的度数．
11．如图，AB∥CD，∠1＝115°，∠2＝140°．求∠3的度数．
12．如图，已知AB∥CD，AD∥BC，判断∠1与∠2是否相等，并说明理由．
13．如图，AB∥DE∥CF，若∠ABC＝80°，∠CDE＝135°，求∠BCD的度数．
14．如图，EF∥AD，∠1＝∠2，∠BAC＝80°．求∠AGD的度数．
15．我们已经学习了平行线的判定条件与相关性质．涉及同位角、内错角、同旁内角．如图①，在“三线八角”中，类比内错角，具有∠1与∠8这样位置关系的角称为“外错角”，试完成下面的探究问题．
（1）探究定义：如图①，请另找出一对“外错角”： ．
（2）猜想判定：外错角相等，两直线平行．
如图②，∠1与∠2是直线a、b被直线c截出的一对外错角，且∠1＝∠2，试说明a∥b．
（3）猜想性质：两直线平行，外错角相等．
如图②，∠1与∠2是直线a、b被直线c截出的一对外错角，且a∥b，试说明∠1＝∠2．
参考答案与试题解析
一、选择题
1．【分析】根据平行线的性质进行解答便可．
【解答】解：∵a∥b，
∴∠1＝∠2，
∵∠1＝58°，
∴∠2＝58°，
故选：C．
2．【分析】根据AB∥CD可得∠CHG＝∠AGE，再根据平角的性质可求∠DHG．
【解答】解：∵AB∥CD，
∴∠CHG＝∠AGE＝100°．
∴∠DHG＝180°﹣∠CHE＝80°．
故选：B．
3．【分析】根据平行线的性质即可得到结论．
【解答】解：∵l1∥l2，
∴α＝49°，
故选：B．
4．【分析】先根据图得出∠2的补角，再由a∥b得出结论即可．
【解答】解：由图得∠2的补角和∠1是同位角，
∵∠1＝60°且a∥b，
∴∠1的同位角也是60°，
∠2＝180°﹣60°＝120°，
故选：D．
5．【分析】根据平行线的性质即可得到结论．
【解答】解：∵l1∥l2，∠1＝70°，
∴∠3＝∠1＝70°，
∵l3∥l4，
∴∠2＝180°﹣∠3＝180°﹣70°＝110°，
故选：B．
6．【分析】根据两直线平行，同位角相等得到∠4的度数，再根据两直线平行，同位角相等即可得到∠3的度数．
【解答】解：如图，
∵l4∥l1，
∴∠4＝∠1＝36°，
∴∠3＝∠4+∠2＝92°．
故选：A．
7．【分析】作平行于两条平行线的直线l，根据∠1+∠2＝∠3+∠4＝60°，计算求解即可．
【解答】解：如图，作平行于两条平行线的直线l，
由平行线的性质可得，∠1＝∠3，∠2＝∠4，
∴∠1+∠2＝∠3+∠4＝60°，
∵∠1＝35°，
∴∠2＝25°．
故选：A．
二、填空题
8．【分析】直接利用平行线的性质结合垂直定义得出∠BAC度数以及∠ACD的度数．
【解答】解：∵AB⊥AE，∠CAE＝38°，
∴∠BAC＝90°﹣38°＝52°，
∵AB∥CD，
∴∠BAC+∠ACD＝180°，
∴∠ACD＝128°．
故答案为：128°．
三、解答题
9．【分析】由AC与DF平行，AB与EF平行，利用两直线平行内错角得到两对内错角相等，等量代换得到∠1＝∠2，即可求出∠1的度数．
【解答】解：∵AC∥DF，
∴∠2＝∠F，
∵AB∥EF，
∴∠1＝∠F，
∴∠1＝∠2＝50°．
10．【分析】（1）根据平行线的性质得∠ACB＝AED＝80°，再根据角平分线的定义得∠ACD＝∠ACB＝40°；
（2）根据三角形外角性质得∠AED＝∠ACD+∠EDC，然后把∠AED＝80°，∠ACD＝40°代入计算即可．
【解答】解：（1）∵DE∥BC，
∴∠ACB＝∠AED，
而∠AED＝80°，
∴∠ACB＝80°，
∵CD平分∠ACB，
∴∠ACD＝∠ACB＝40°；
（2）∵∠AED＝∠ACD+∠EDC，
∴∠EDC＝80°﹣40°＝40°．
11．【分析】连接AC，由∠1＝115°，∠2＝140°，可求出∠1+∠2＝255°，然后由AB∥CD，可得∠BAC+∠ACD＝180°，从而可求∠EAC+∠ECA＝255°﹣180°＝75°，然后根据外角的性质可求∠3的度数．
【解答】解：连接AC，
∵∠1＝115°，∠2＝140°，
∴∠1+∠2＝255°，
∵AB∥CD，
∴∠BAC+∠ACD＝180°，
∴∠EAC+∠ECA＝∠1+∠2﹣（∠BAC+∠ACD）
＝255°﹣180°＝75°，
∵∠3是△AEC的外角，
∴∠3＝∠EAC+∠ECA＝75°．
12．【分析】先根据AB∥CD得出∠1＝∠3，再根据AD∥BC得出∠3＝∠2，故可得出结论．
【解答】解：∠1＝∠2．
理由：∵AB∥CD，
∴∠1＝∠3，
∵AD∥BC，
∴∠3＝∠2，
∴∠1＝∠2．
13．【分析】由平行线的性质可求得∠BCF和∠DCF的值，可求得∠BCD．
【解答】解：∵AB∥CF，∠ABC＝80°，
∴∠BCF＝∠ABC＝80°，
∵DE∥CF，
∴∠DCF+∠CDE＝180°，
∵∠CDE＝135°，
∴∠DCF＝180°﹣∠CDE＝180°﹣135°＝45°，
∴∠BCD＝∠BCF﹣∠DCF＝80°﹣45°＝35°．
14．【分析】根据两直线平行，同位角相等可得∠2＝∠3，然后求出∠1＝∠3，再根据内错角相等，两直线平行判断出DG∥AB，然后根据两直线平行，同旁内角互补解答．
【解答】解：∵EF∥AD，
∴∠2＝∠3，
∵∠1＝∠2，
∴∠1＝∠3，
∴DG∥AB，
∴∠AGD＝180°﹣∠BAC＝180°﹣80°＝100°．
15．【分析】（1）根据“外错角”的定义结合图形即可得出结论；
（2）根据对顶角相等即可得出∠1＝∠3，结合∠1＝∠2即可得出∠2＝∠3，再根据“同位角相等，两直线平行”即可证出a∥b；
（3）模仿（2）写出已知及求证，由a∥b利用“两直线平行，同位角相等”即可得出∠2＝∠3，再由对顶角相等可得出∠1＝∠3，由此即可证出∠1＝∠2．
【解答】解：（1）∵∠1与∠8这样位置关系的角称为“外错角”，
∴∠2和∠7也为“外错角”．
故答案为：∠2和∠7．
（2）证明：∵∠1＝∠3（对顶角相等），∠1＝∠2（已知），
∴∠2＝∠3（等量替换），
∴a∥b（同位角相等，两直线平行）．
（3）证明：∵a∥b（已知），
∴∠2＝∠3（两直线平行，同位角相等），
∵∠1＝∠3（对顶角相等），
∴∠1＝∠2（等量替换）．