鲁教版（五四学制）（2024）九年级下册7 切线长定理精练

这是一份鲁教版（五四学制）（2024）九年级下册7 切线长定理精练，共8页。
1．如图，⊙O是△ABC的内切圆，点D、E分别为边AB、AC上的点，且DE为⊙O的切线，若△ABC的周长为25，BC的长是9，则△ADE的周长是（ ）
A．7B．8C．9D．16
2．如图PA、PB、CD分别切⊙O于A、B、E，∠APB＝54°，则∠COD＝（ ）
A．36°B．63°C．126°D．46°
3．如图，△ABC是一张周长为17cm的三角形的纸片，BC＝5cm，⊙O是它的内切圆，小明准备用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN，则剪下的三角形的周长为（ ）
A．12cm
B．7cm
C．6cm
D．随直线MN的变化而变化
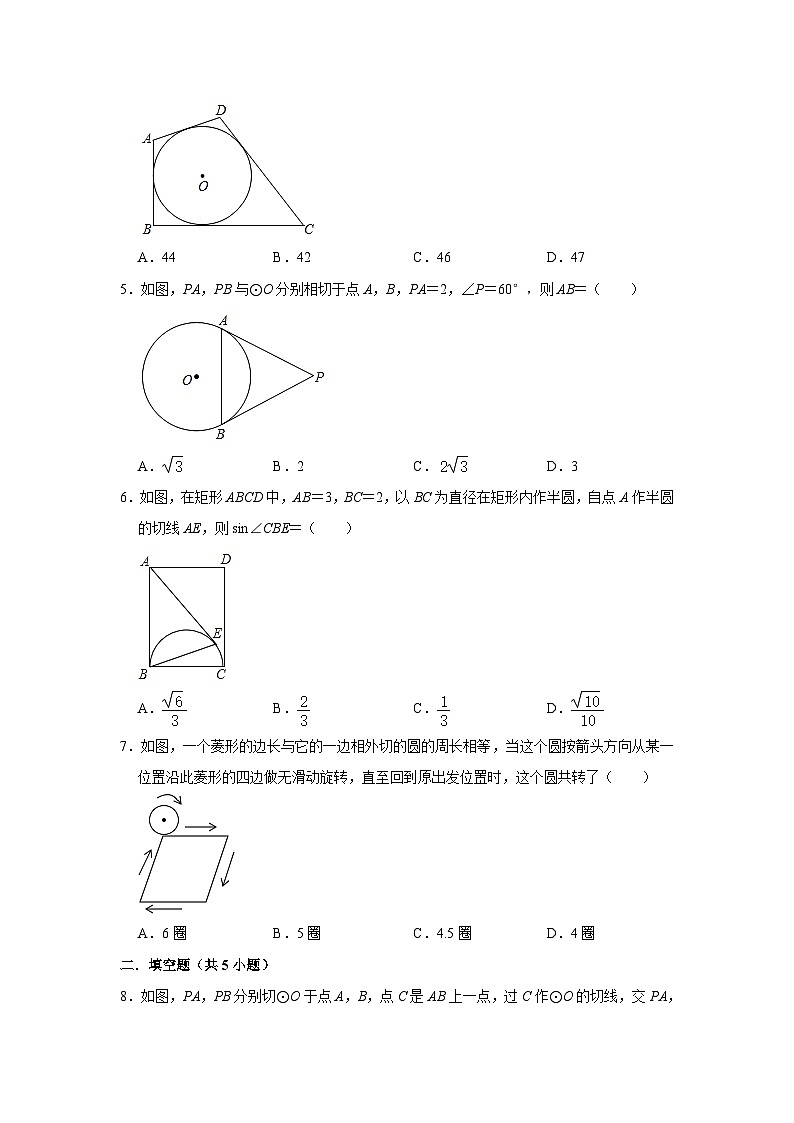
4．如图，四边形ABCD是⊙O的外切四边形，且AB＝10，CD＝12，则四边形ABCD的周长为（ ）
A．44B．42C．46D．47
5．如图，PA，PB与⊙O分别相切于点A，B，PA＝2，∠P＝60°，则AB＝（ ）
A．B．2C．D．3
6．如图，在矩形ABCD中，AB＝3，BC＝2，以BC为直径在矩形内作半圆，自点A作半圆的切线AE，则sin∠CBE＝（ ）
A．B．C．D．
7．如图，一个菱形的边长与它的一边相外切的圆的周长相等，当这个圆按箭头方向从某一位置沿此菱形的四边做无滑动旋转，直至回到原出发位置时，这个圆共转了（ ）
A．6圈B．5圈C．4.5圈D．4圈
二．填空题（共5小题）
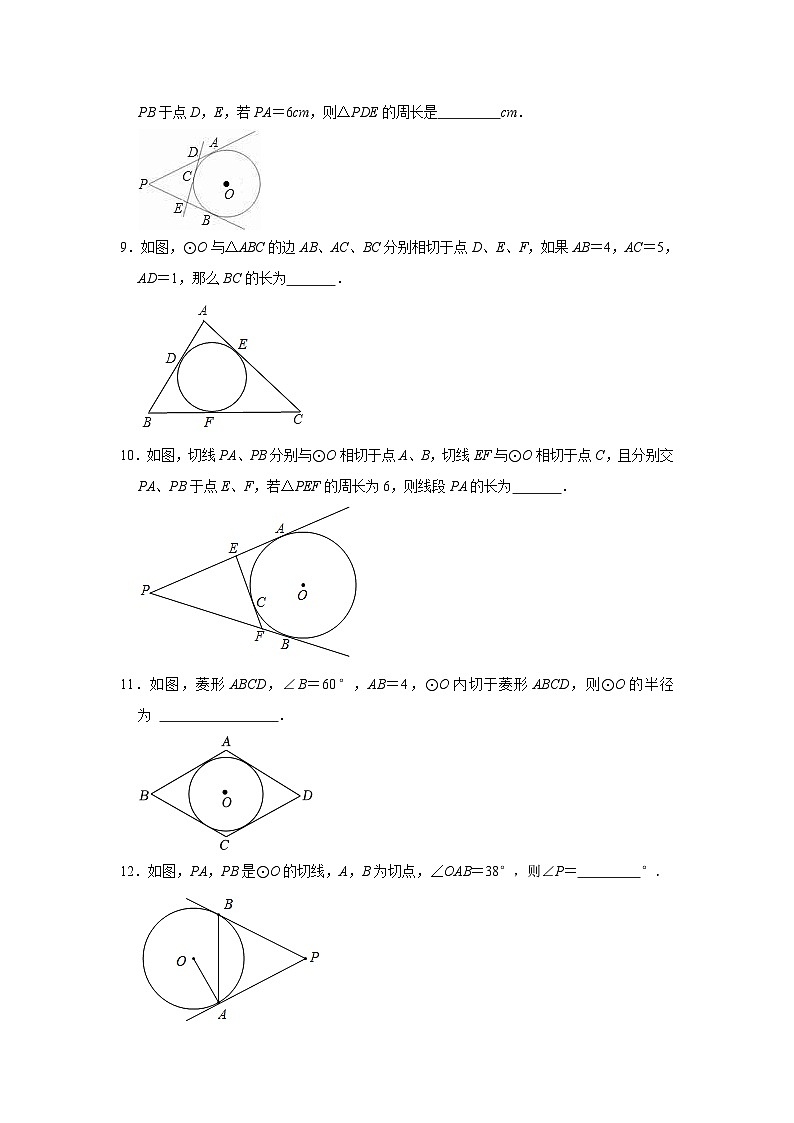
8．如图，PA，PB分别切⊙O于点A，B，点C是AB上一点，过C作⊙O的切线，交PA，PB于点D，E，若PA＝6cm，则△PDE的周长是 cm．
9．如图，⊙O与△ABC的边AB、AC、BC分别相切于点D、E、F，如果AB＝4，AC＝5，AD＝1，那么BC的长为 ．
10．如图，切线PA、PB分别与⊙O相切于点A、B，切线EF与⊙O相切于点C，且分别交PA、PB于点E、F，若△PEF的周长为6，则线段PA的长为 ．
11．如图，菱形ABCD，∠B＝60°，AB＝4，⊙O内切于菱形ABCD，则⊙O的半径为 ．
12．如图，PA，PB是⊙O的切线，A，B为切点，∠OAB＝38°，则∠P＝ °．
三．解答题（共5小题）
13．如图，PA和PB是⊙O的两条切线，A，B是切点．C是弧AB上任意一点，过点C画⊙O的切线，分别交PA和PB于D，E两点，已知PA＝PB＝5cm，求△PDE的周长．
14．如图，PA、PB是⊙O的切线，CD切⊙O于点E，△PCD的周长为12，∠APB＝60°．求：
（1）PA的长；
（2）∠COD的度数．
15．如图，∠APB＝52°，PA、PB、DE都为⊙O的切线，切点分别为A、B、F，且PA＝6．
（1）求△PDE的周长；
（2）求∠DOE的度数．
16．如图，PA，PB是⊙O的切线，A、B为切点，AC是⊙O的直径，∠P＝60°．
（1）求∠BAC的度数；
（2）当OA＝2时，求AB的长．
17．如图，直线AB、BC、CD分别与⊙O相切于E、F、G，且AB∥CD，OB＝6cm，OC＝8cm．求：
（1）∠BOC的度数；
（2）BE+CG的长；
（3）⊙O的半径．
答案
一．选择题（共7小题）
1．A
2．B
3．B
4．A
5．B
6．D
7．B
二．填空题（共5小题）
8．12cm
9．7
10．3．
11．．
12．76
三．解答题（共5小题）
13．10cm．
14．（1）6；
（2）∵∠P＝60°，
∴∠PCE+∠PDE＝120°，
∴∠ACD+∠CDB＝360°﹣120°＝240°，
∵CA，CE是圆O的切线，
∴∠OCE＝∠OCA＝∠ACD；
同理：∠ODE＝∠CDB，
∴∠OCE+∠ODE＝（∠ACD+∠CDB）＝120°，
∴∠COD＝180﹣120°＝60°．
15．解：（1）∵PA、PB、DE都为⊙O的切线，
∴DA＝DF，EB＝EF，PA＝PB＝6，
∴DE＝DA+EB，
∴PE+PD+DE＝PA+PB＝12，
即△PDE的周长为12；
（2）连接OF，
∵PA、PB、DE分别切⊙O于A、B、F三点，
∴OB⊥PB，OA⊥PA，∠BOE＝∠FOE＝∠BOF，∠FOD＝∠AOD＝∠AOF，
∵∠APB＝52°，
∴∠AOB＝360°﹣90°﹣90°﹣52°＝128°，
∴∠DOE＝∠FOE+∠FOD＝（∠BOF+∠AOF）＝∠BOA＝64°．
16．
解：（1）∵PA，PB是⊙O的切线，
∴AP＝BP，
∵∠P＝60°，
∴∠PAB＝60°，
∵AC是⊙O的直径，
∴∠PAC＝90°，
∴∠BAC＝90°﹣60°＝30°．
（2）连接OP，则在Rt△AOP中，OA＝2，∠APO＝30°，
∴OP＝4，
由勾股定理得：，
∵AP＝BP，∠APB＝60°，
∴△APB是等边三角形，
∴．
17．
解：（1）连接OF；根据切线长定理得：BE＝BF，CF＝CG，∠OBF＝∠OBE，∠OCF＝∠OCG；
∵AB∥CD，
∴∠ABC+∠BCD＝180°，
∴∠OBF+∠OCF＝90°，
∴∠BOC＝90°；
（2）由（1）知，∠BOC＝90°．
∵OB＝6cm，OC＝8cm，
∴由勾股定理得到：BC＝＝10cm，
∴BE+CG＝BC＝10cm．
（3）∵BC与⊙O相切于点F，
∴OF⊥BC，
∴S△OBC＝OF×BC＝OB×OC，即OF×10＝×6×8．
∴OF＝4.8cm．