初中数学鲁教版（五四学制）（2024）九年级下册2 圆的对称性当堂达标检测题

这是一份初中数学鲁教版（五四学制）（2024）九年级下册2 圆的对称性当堂达标检测题，共9页。试卷主要包含了下列说法中，正确的是等内容，欢迎下载使用。
1．下列说法中，正确的是（ ）
A．同心圆的周长相等
B．面积相等的圆是等圆
C．相等的圆心角所对的弧相等
D．平分弧的弦一定经过圆心
2．如图，已知在⊙O中，BC是直径，AB＝DC，则下列结论不一定成立的是（ ）
A．OA＝OB＝ABB．∠AOB＝∠COD
C．D．O到AB、CD的距离相等
3．如图，AB是⊙O的直径，＝＝，若∠COD＝35°，则∠AOE的度数是（ ）
A．35°B．55°C．75°D．95°
4．如图，已知AC是直径，AB＝6，BC＝8，D是弧BC的中点，则DE＝（ ）
A．1B．2C．3D．4
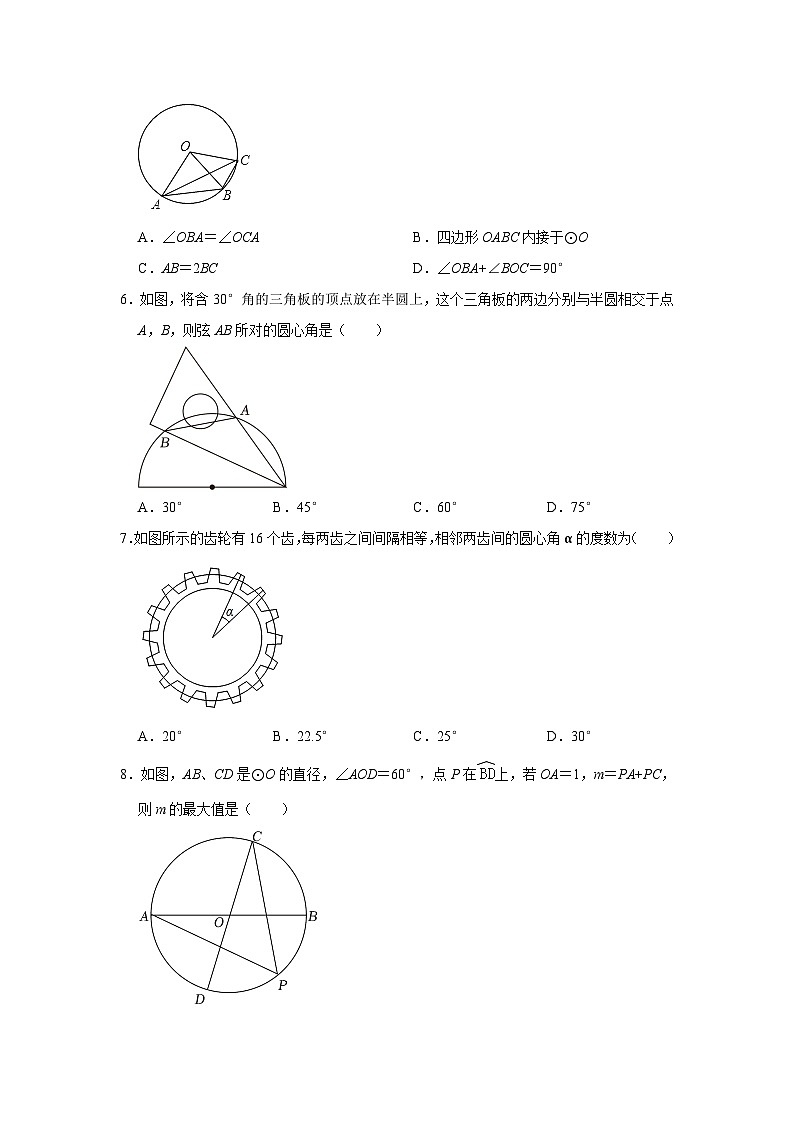
5．如图，A，B，C是⊙O上三个点，∠AOB＝2∠BOC，则下列说法中正确的是（ ）
A．∠OBA＝∠OCAB．四边形OABC内接于⊙O
C．AB＝2BCD．∠OBA+∠BOC＝90°
6．如图，将含30°角的三角板的顶点放在半圆上，这个三角板的两边分别与半圆相交于点A，B，则弦AB所对的圆心角是（ ）
A．30°B．45°C．60°D．75°
7．如图所示的齿轮有16个齿，每两齿之间间隔相等，相邻两齿间的圆心角α的度数为（ ）
A．20°B．22.5°C．25°D．30°
8．如图，AB、CD是⊙O的直径，∠AOD＝60°，点P在上，若OA＝1，m＝PA+PC，则m的最大值是（ ）
A．2B．2C．4D．2
二．填空题（共4小题）
9．如图，在⊙O中，AB＝8，C为的中点，且C到AB的距离为3，则圆的半径为 ．
10．如图，在半径为10的圆O中，∠AOB＝90°，C为OB的中点，AC的延长线交圆O于点D，则线段CD的长为 ．
11．只用一张矩形纸条和刻度尺，如何测量一次性纸杯杯口的直径？小聪同学所在的学习小组想到了如下方法：如图，将纸条拉直紧贴杯口上，纸条的上下边沿分别与杯口相交于A，B，C，D四点，利用刻度尺量得该纸条宽MN为7cm，AB＝6cm，CD＝8cm．请你帮忙计算纸杯的直径为 cm．
12．如图所对圆心角∠AOB＝90°，半径为4，C是OB的中点，D是上一点，把CD绕点C逆时针旋转90°得到CE，连接AE，则AE的最小值是 ．
三．解答题（共5小题）
13．如图，A、B、C、D是⊙O上四点，且AD＝CB，求证：AB＝CD．
14．如图，在△ABC中，以点A为圆心画弧分别交AB，BA的延长线和AC于D，E，F，连接EF并延长交BC于G，EG⊥BC．
（1）求证：AB＝AC；
（2）连接DF，判断DF与BC的位置关系，并说明理由．
15．如图，AB是⊙O的直径，点C，D是⊙O上的点，且OD∥BC，AC分别与BD．OD相交于点E，F．
（1）求证：点D为弧AC的中点；
（2）若DF＝4，AC＝16，求⊙O的直径．
16．如图，AB，AC是⊙O的两条弦，且＝．
（1）求证：AO平分∠BAC；
（2）若AB＝4，BC＝8，求半径OA的长．
17．如图，以平行四边形ABCD的顶点A为圆心，AB为半径作⊙A，分别交BC、AD于E、F两点，交BA的延长线于点G．
（1）求证：＝；
（2）若为140°，求∠EGB的度数．
参考答案
一．选择题（共8小题）
1．B
2．A
3．C
4．B
5．D
6．C
7．B
8．D
二．填空题（共4小题）
9．．
10．3．
11．10．
12．2﹣4．
三．解答题（共5小题）
13．证明：∵AD＝CB，
∴＝，
∴+＝+，
即＝，
∴AB＝CD．
14．（1）证明：∵EG⊥BC，
∴∠E+∠B＝90°，∠CFG+∠C＝90°，
∵AE＝AF，
∴∠E＝∠AFE，
又∵∠AFE＝∠CFG，
∴∠E＝∠CFG，
∴∠B＝∠C，
∴AB＝AC；
（2）解：DF与BC的位置关系是DF∥BC，理由如下：
连接DF，如图所示：
依题意得：ED为半圆的直径，∴∠EFD＝90°，
即BF⊥EG，
又∵EG⊥BC，
∴DF∥BC．
15．（1）证明：∵AB是⊙O的直径，
∴∠ACB＝90°，
∵OD∥BC，
∴∠OFA＝∠C＝90°，
∴OF⊥AC，
∴＝，
∴点D为的中点；
（2）解：∵OF⊥AC，
∴AF＝AC＝8，
在Rt△AFO中，AO2＝AF2+OF2，
∴OA2＝64+（OD﹣DF）2，
∴OA2＝64+（OA﹣4）2，
∴OA＝10，
∴⊙O的直径为20．
16．证明：（1）连接OB、OC，
∵＝．
∴AB＝AC，
∵OC＝OB，OA＝OA，
在△AOB与△AOC中，
．
∴△AOB≌△AOC（SSS），
∴∠1＝∠2，
∴AO平分∠BAC；
（2）连接AO并延长交BC于E，连接OB，
∵AB＝AC，AO平分∠BAC，
∴AE⊥BC，
设OA＝x，可得：AB2﹣BE2＝AE2，OB2＝OE2+BE2，
可得：，x2＝OE2+42，OE+x＝8，
解得：x＝5，OE＝3，
∴半径OA的长＝5．
17．（1）证明：连接AE．
∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠EAF＝∠AEB，∠GAF＝∠B，
∵AE＝AB，
∴∠B＝∠AEB，
∴∠EAF＝∠GAF，
∴＝；
（2）∵GB为⊙A的直径，
∴为180°，
∵为140°，
∴为40°，
∴∠BAE＝40°
∵∠EGB＝∠BAE，
∴∠EGB＝20°．