

2024-2025学年人教版数学八年级上册期末 模拟练习 (真题重组卷)
展开
这是一份2024-2025学年人教版数学八年级上册期末 模拟练习 (真题重组卷),共24页。
A.B.
C.D.
2.(2023秋•娄星区期末)用直尺和圆规作一个角等于已知角,如图,能得出∠AOB=∠A′O′B′的依据是( )
A.SSSB.SASC.ASAD.AAS
3.(2024春•太康县期末)下面各组线段中,能组成三角形的是( )
A.5,11,6B.8,8,16C.10,5,4D.6,9,14
4.(2022秋•天桥区期末)如图,在△ABC中,PM、QN分别是线段AB、AC的垂直平分线,若∠BAC=110°,则∠PAQ的度数是( )
A.40°B.50°C.60°D.70°
5.(2024春•连州市期末)三条公路将A、B、C三个村庄连成一个如图的三角形区域,如果在这个区域内修建一个公园,要使公园到三个村庄的距离相等,那么这个公园应建的位置是△ABC的( )
A.三条高线的交点
B.三边垂直平分线的交点
C.三条角平分线的交点
D.三条中线的交点
6.(2023秋•绥阳县期末)如图,衣架框内部可以近似看成一个等腰三角形,记为等腰三角形ABC,若AB=AC=26cm,D是BC的中点,∠ABC=30°,则AD的长为( )
A.11cmB.12cmC.13cmD.14cm
7.(2022秋•鹤壁期末)将几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式,例如,由图1可得等式:x2+(p+q)x+pq=(x+p)(x+q).将图2所示的卡片若干张进行拼图,可以将二次三项式a2+3ab+2b2分解因式为( )
A.(a+b)(2a+b)B.(a+b)(3a+b)
C.(a+b)(a+2b)D.(a+b)(a+3b)
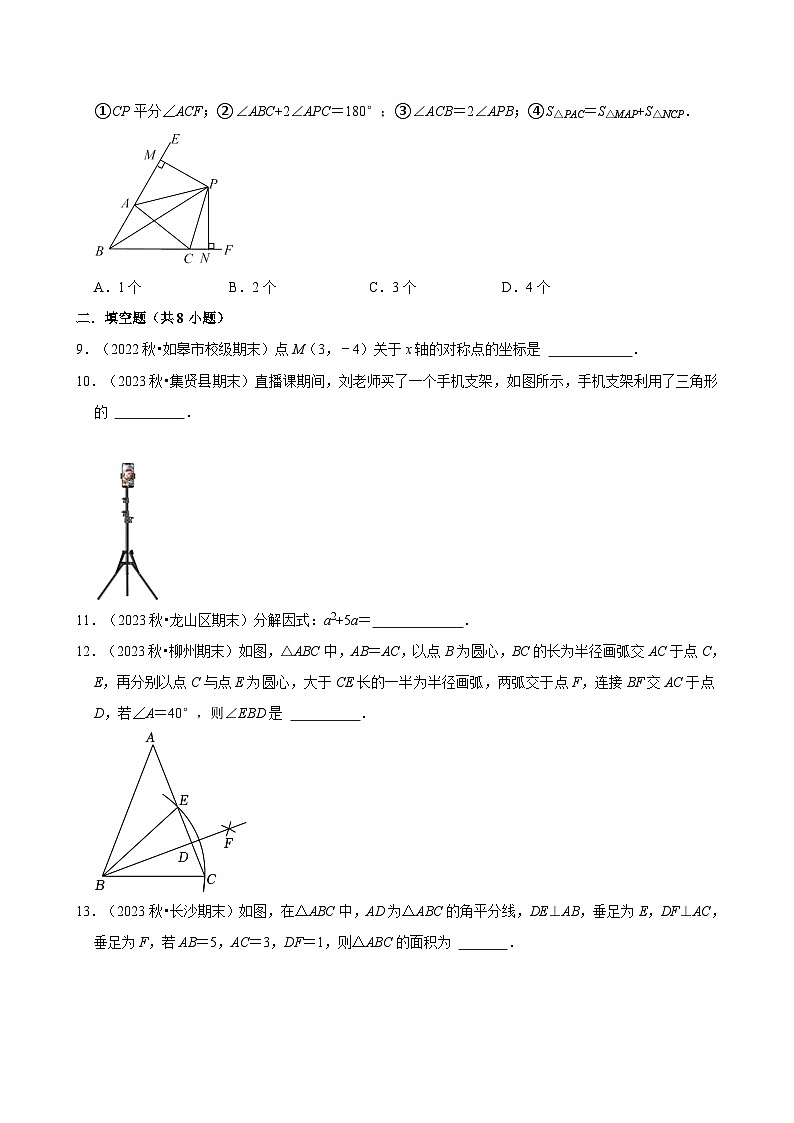
8.(2023秋•廉江市期末)如图,△ABC中,∠ABC、∠EAC的角平分线BP、AP交于点P,延长BA、BC,PM⊥BE,PN⊥BF,则下列结论中正确的个数( )
①CP平分∠ACF;②∠ABC+2∠APC=180°;③∠ACB=2∠APB;④S△PAC=S△MAP+S△NCP.
A.1个B.2个C.3个D.4个
二.填空题(共8小题)
9.(2022秋•如皋市校级期末)点M(3,﹣4)关于x轴的对称点的坐标是 .
10.(2023秋•集贤县期末)直播课期间,刘老师买了一个手机支架,如图所示,手机支架利用了三角形的 .
11.(2023秋•龙山区期末)分解因式:a2+5a= .
12.(2023秋•柳州期末)如图,△ABC中,AB=AC,以点B为圆心,BC的长为半径画弧交AC于点C,E,再分别以点C与点E为圆心,大于CE长的一半为半径画弧,两弧交于点F,连接BF交AC于点D,若∠A=40°,则∠EBD是 .
13.(2023秋•长沙期末)如图,在△ABC中,AD为△ABC的角平分线,DE⊥AB,垂足为E,DF⊥AC,垂足为F,若AB=5,AC=3,DF=1,则△ABC的面积为 .
14.(2024春•榆阳区期末)如图,在△ABC中,BO平分∠ABC,OD⊥BC于点D,连接OA,若OD=3,AB=12,则△AOB的面积是 .
15.(2023秋•东城区期末)如图,Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=6,D是线段AB上一个动点,以BD为边在△ABC外作等边△BDE.若F是DE的中点,当CF取最小值时,△BDE的周长为 .
16.(2023秋•旌阳区期末)为了庆祝神舟十五号的成功发射,学校组织了一次小制作展示活动,小明计划制作一个如图所示的简易模型,已知该模型满足△ABD≌△ACE,点B和点C是对应顶点,若AB=8cm,AD=3cm,则DC= cm.
三.解答题(共7小题)
17.(2024春•高碑店市期末)如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°,求:
(1)∠BAE的度数;
(2)∠DAE的度数.
18.(2024春•中宁县期末)如图,在Rt△ABC中,∠B=90°.
(1)尺规作图:作∠A的角平分线AP,交BC于点D.(基本作图,保留作图痕迹,不写作法,并标明字母)
(2)若AB=3,BC=4,求BD的长及△ACD的面积.
19.(2024春•玉溪期末)如图,已知AB=AD,AC=AE,∠BAD=∠CAE,求证:△ABC≌△ADE.
20.(2024春•西安期末)如图,在△ABC中,∠ABC、∠ACB的平分线交于点D,延长BD交AC于E,G、F分别在BD、BC上,连接DF、GF,其中∠A=2∠BDF,GD=DE.
(1)当∠A=80°时,求∠EDC的度数;
(2)求证:CF=FG+CE.
21.(2024春•商水县期末)阅读下列材料,并完成相应的任务:
任务:(1)将凹四边形的内角和为360°的证明过程补充完整.
(2)如图3,在凹四边形ABCD中,求证:∠BCD=∠BAD+∠B+∠D.
(3)如图4,在四边形ABCD中,已知∠A=70°,∠B=28°,∠BCD=150°,求∠D的度数.
22.(2023秋•临颍县期末)实践与探索
如图1,边长为a的大正方形有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示).
(1)上述操作能验证的等式是 ;(请选择正确的一个)
A.a2﹣b2=(a+b)(a﹣b)
B.a2﹣2ab+b2=(a﹣b)2
C.a2+ab=a(a+b)
(2)请应用这个公式完成下列各题:
①已知4a2﹣b2=24,2a+b=6,则2a﹣b= .
②计算:1002﹣992+982﹣972+…+42﹣32+22﹣12.
23.(2023秋•佛山期末)已知∠AOB=90°,直线CD与OA交于点C,与OB交于点D,点C,D均不与点O重合,CE平分∠DCO,DE平分∠CDO.
(1)如图1,当∠OCD=40°时,求∠CED的度数;
(2)如图2,延长CE与BO交于点F,过E作射线EG与CD交于点G,且满足∠CFO﹣∠GED=45°.求证:GE∥DO;
(3)如图3,过点C作CM⊥CN,MN是∠COD的外角平分线所在直线,与射线CE交于点N,与CM交于点M.在△CMN中,如果有一个角的度数是另一个角的3倍,请直接写出∠CDE的度数.
期末真题重组卷-2024-2025学年数学八年级上册人教版
参考答案与试题解析
一.选择题(共8小题)
1.(2023秋•通河县期末)下面四幅作品分别代表“立春”、芒种”、“白露”、“大雪”四个节气,其中是轴对称图形的是( )
A.B.
C.D.
【解答】解:A、不是轴对称图形
B、不是轴对称图形
C、不是轴对称图形
D、是轴对称图形;
故选:D.
2.(2023秋•娄星区期末)用直尺和圆规作一个角等于已知角,如图,能得出∠AOB=∠A′O′B′的依据是( )
A.SSSB.SASC.ASAD.AAS
【解答】解:在△ODC和△O′D′C′中,
,
∴△ODC≌△O′C′D′(SSS),
∴∠AOB=∠A′O′B′.
故选:A.
3.(2024春•太康县期末)下面各组线段中,能组成三角形的是( )
A.5,11,6B.8,8,16C.10,5,4D.6,9,14
【解答】解:A、∵5+6=11,∴不能组成三角形,故A选项错误;
B、∵8+8=16,∴不能组成三角形,故B选项错误;
C、∵5+4<10,∴不能组成三角形,故C选项错误;
D、∵6+9>14,∴能组成三角形,故D选项正确.
故选:D.
4.(2022秋•天桥区期末)如图,在△ABC中,PM、QN分别是线段AB、AC的垂直平分线,若∠BAC=110°,则∠PAQ的度数是( )
A.40°B.50°C.60°D.70°
【解答】解:∵∠BAC=110°,
∴∠B+∠C=180°﹣∠BAC=70°,
∵PM、QN分别是线段AB、AC的垂直平分线,
∴AP=BP,CQ=AQ,
∴∠BAP=∠B,∠CAQ=∠C,
∴∠BAP+∠CAQ=∠B+∠C=70°,
∵∠BAC=110°,
∴∠PAQ=∠BAC﹣(∠BAP+∠CAQ)=110°﹣70°=40°,
故选:A.
5.(2024春•连州市期末)三条公路将A、B、C三个村庄连成一个如图的三角形区域,如果在这个区域内修建一个公园,要使公园到三个村庄的距离相等,那么这个公园应建的位置是△ABC的( )
A.三条高线的交点
B.三边垂直平分线的交点
C.三条角平分线的交点
D.三条中线的交点
【解答】解:∵线段垂直平分线上的点到线段两端的距离相等,
∴这个公园应建的位置是△ABC的三边垂直平分线的交点上.
故选:B.
6.(2023秋•绥阳县期末)如图,衣架框内部可以近似看成一个等腰三角形,记为等腰三角形ABC,若AB=AC=26cm,D是BC的中点,∠ABC=30°,则AD的长为( )
A.11cmB.12cmC.13cmD.14cm
【解答】解:∵AB=AC=26cm,D是BC的中点,
∴AD⊥BC,
∴∠ADB=90°,
∵∠ABC=30°,
∴AD=AB=13(cm),
故选:C.
7.(2022秋•鹤壁期末)将几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式,例如,由图1可得等式:x2+(p+q)x+pq=(x+p)(x+q).将图2所示的卡片若干张进行拼图,可以将二次三项式a2+3ab+2b2分解因式为( )
A.(a+b)(2a+b)B.(a+b)(3a+b)
C.(a+b)(a+2b)D.(a+b)(a+3b)
【解答】解:a2+3ab+2b2=(a+b)(a+2b),
故选:C.
8.(2023秋•廉江市期末)如图,△ABC中,∠ABC、∠EAC的角平分线BP、AP交于点P,延长BA、BC,PM⊥BE,PN⊥BF,则下列结论中正确的个数( )
①CP平分∠ACF;②∠ABC+2∠APC=180°;③∠ACB=2∠APB;④S△PAC=S△MAP+S△NCP.
A.1个B.2个C.3个D.4个
【解答】解:①过点P作PD⊥AC于D,
∵PB平分∠ABC,PA平分∠EAC,PM⊥BE,PN⊥BF,PD⊥AC,
∴PM=PN,PM=PD,
∴PN=PD,
∵PN⊥BF,PD⊥AC,
∴点P在∠ACF的角平分线上,故①正确;
②∵PM⊥AB,PN⊥BC,
∴∠ABC+90°+∠MPN+90°=360°,
∴∠ABC+∠MPN=180°,
在Rt△PAM和Rt△PAD中,
,
∴Rt△PAM≌Rt△PAD(HL),
∴∠APM=∠APD,
同理:Rt△PCD≌Rt△PCN(HL),
∴∠CPD=∠CPN,
∴∠MPN=2∠APC,
∴∠ABC+2∠APC=180°,②正确;
③∵PA平分∠CAE,BP平分∠ABC,
∴∠CAE=∠ABC+∠ACB=2∠PAM,∠PAM=∠ABC+∠APB,
∴∠ACB=2∠APB,③正确;
④由②可知Rt△PAM≌Rt△PAD(HL),Rt△PCD≌Rt△PCN(HL)
∴S△APD=S△APM,S△CPD=S△CPN,
∴S△APM+S△CPN=S△APC,故④正确,
故选:D.
二.填空题(共8小题)
9.(2022秋•如皋市校级期末)点M(3,﹣4)关于x轴的对称点的坐标是 (3,4) .
【解答】解:点M(3,﹣4)关于x轴的对称点M′的坐标是(3,4).
故答案为:(3,4).
10.(2023秋•集贤县期末)直播课期间,刘老师买了一个手机支架,如图所示,手机支架利用了三角形的 稳定性 .
【解答】解:手机支架利用了三角形的稳定性,
故答案为:稳定性.
11.(2023秋•龙山区期末)分解因式:a2+5a= a(a+5) .
【解答】解:∵a2+5a公有因式为a,
∴原式=a(a+5),
故答案为:a(a+5).
12.(2023秋•柳州期末)如图,△ABC中,AB=AC,以点B为圆心,BC的长为半径画弧交AC于点C,E,再分别以点C与点E为圆心,大于CE长的一半为半径画弧,两弧交于点F,连接BF交AC于点D,若∠A=40°,则∠EBD是 20° .
【解答】解:∵AB=AC,∠A=40°,
∴∠ACB=(180°﹣40°)÷2=70°,
由题意可知,BC=BE,
∴∠BEC=∠ACB=70°,
∴∠CBE=180°﹣70°×2=40°,
∴∠EBD=∠CBE=20°.
故答案为:20°.
13.(2023秋•长沙期末)如图,在△ABC中,AD为△ABC的角平分线,DE⊥AB,垂足为E,DF⊥AC,垂足为F,若AB=5,AC=3,DF=1,则△ABC的面积为 4 .
【解答】解:∵AD为△ABC的角平分线,DE⊥AB,垂足为E,DF⊥AC,垂足为F,
∴DE=DF=1,
∵AB=5,AC=3,
∴S△ABC=S△ABD+S△ACD
=AB•DE+AC•DF
=×5×1+×3×1
=+
=4.
故答案为:4.
14.(2024春•榆阳区期末)如图,在△ABC中,BO平分∠ABC,OD⊥BC于点D,连接OA,若OD=3,AB=12,则△AOB的面积是 18 .
【解答】解:如图,过点O作OE⊥AB于点E,
∵BO平分∠ABC,OD⊥BC,
∴OE=OD=3,
∴△AOB的面积=,
故答案为:18.
15.(2023秋•东城区期末)如图,Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=6,D是线段AB上一个动点,以BD为边在△ABC外作等边△BDE.若F是DE的中点,当CF取最小值时,△BDE的周长为 18 .
【解答】解:连接BF,过点C作CH⊥BF.交BF的延长线于H,
∵△BDE是等边三角形,点F是DE的中点,
∴∠ABF=30°,
∴点F在射线BF上运动,
当点F与点H重合时,CF最小,
∵∠ACB=90°,∠ABC=30°,
∴∠A=60°,AB=2AC=12,
∵∠ABF=30°,
∴∠BD'H=∠AD'C=60°,
∴△ACD'是等边三角形,
∴AD'=AC=6,
∴BD'=AB﹣AD'=12﹣6=6,
∴△BDE的周长为:18,
故答案为:18.
16.(2023秋•旌阳区期末)为了庆祝神舟十五号的成功发射,学校组织了一次小制作展示活动,小明计划制作一个如图所示的简易模型,已知该模型满足△ABD≌△ACE,点B和点C是对应顶点,若AB=8cm,AD=3cm,则DC= 5 cm.
【解答】解:∵△ABD≌△ACE,
∴AC=AB=8cm,
∵AD=3cm,
∴CD=AC﹣AD=5(cm).
故答案为:5.
三.解答题(共7小题)
17.(2024春•高碑店市期末)如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°,求:
(1)∠BAE的度数;
(2)∠DAE的度数.
【解答】解:(1)∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°﹣∠B﹣∠C
=180°﹣70°﹣30°
=80°.
∵AE平分∠BAC,
∴.
(2)∵AD⊥BC,
∴∠ADB=90°,
∴∠BAD=90°﹣∠B
=90°﹣70°
=20°.
∴∠DAE=∠BAE﹣∠BAD
=40°﹣20°
=20°.
18.(2024春•中宁县期末)如图,在Rt△ABC中,∠B=90°.
(1)尺规作图:作∠A的角平分线AP,交BC于点D.(基本作图,保留作图痕迹,不写作法,并标明字母)
(2)若AB=3,BC=4,求BD的长及△ACD的面积.
【解答】解:(1)如图,AP即为所求;
(2)在Rt△ABC中,由勾股定理得,AC==,
由(1)知,AD平分∠BAC,
∴点D到AC的距离=BD的长
设BD=x,
∴=,
解得x=,
∴BD=,
∴S△ACD==.
19.(2024春•玉溪期末)如图,已知AB=AD,AC=AE,∠BAD=∠CAE,求证:△ABC≌△ADE.
【解答】证明:∵∠BAD=∠CAE,
∴∠BAD+∠DAC=∠CAE+∠DAC,即∠BAC=∠DAE,
在△ABC和△ADE中,
,
∴△ABC≌△ADE(SAS).
20.(2024春•西安期末)如图,在△ABC中,∠ABC、∠ACB的平分线交于点D,延长BD交AC于E,G、F分别在BD、BC上,连接DF、GF,其中∠A=2∠BDF,GD=DE.
(1)当∠A=80°时,求∠EDC的度数;
(2)求证:CF=FG+CE.
【解答】(1)解:方法一:∵∠A=80°,
∴∠ABC+∠ACB=100°,
∵BE平分∠ABC、CD平分∠ACB,
∴∠DBC+∠DCB=50°,
∴∠EDC=∠DBC+∠DCB=50°;
方法二:如图,在BC上取点M,使CM=CE,
∵CD平分∠ACB,
∴∠ACD=∠BCD,
在△CDE和△CDM中,
,
∴△CDE≌△CDM(SAS),
∴DE=DM,∠DEC=∠DMC,∠EDC=∠MDC,
∵GD=DE,
∴GD=MD,
∵∠DEC+∠AEB=180°,∠DMC+∠DMF=180°,
∴∠AEB=∠DMF,
∵BE平分∠ABC,
∴∠ABE=∠CBE=ABC,
∴∠BDM=180°﹣ABC﹣∠DMB=180°﹣ABC﹣∠AEB=∠A=80°,
∴∠EDM=100°,
∴∠EDC=50°;
(2)证明:∵∠A=2∠BDF,
∴∠BDM=2∠BDF,
∴∠FDM=∠BDF,
在△DGF和△DMF中,
,
∴△DGF≌△DMF(SAS),
∴GF=MF,
∴CF=CM+FM=CE+GF.
∴CF=FG+CE.
21.(2024春•商水县期末)阅读下列材料,并完成相应的任务:
任务:(1)将凹四边形的内角和为360°的证明过程补充完整.
(2)如图3,在凹四边形ABCD中,求证:∠BCD=∠BAD+∠B+∠D.
(3)如图4,在四边形ABCD中,已知∠A=70°,∠B=28°,∠BCD=150°,求∠D的度数.
【解答】解:(1)∵∠DAC+∠D+∠ACD=180°,
∵凹四边形的内角和=∠BAC+∠B+∠ACB+∠DAC+∠D+∠ACD,
∴∠BAC+∠B+∠ACB+∠DAC+∠D+∠ACD=360°,
∴∠BAD+∠B+∠α+∠D=360°,
∴凹四边形ABCD的内角和为360°.
(2)∵∠BAD+∠B+∠α+∠D=360°,
∴∠BAD+∠B+∠D=360°﹣∠α.
∵∠α+∠BCD=360°,
∴∠BCD=360°﹣∠α,
∴∠BCD=∠BAD+∠B+∠D.
(3)由(2)可知,∠BCD=∠A+∠B+∠D.
∵∠A=70°,∠B=28°,∠BCD=150°,
∴150°=70°+28°+∠D,
∴∠D=150°﹣70°﹣28°=52°.
22.(2023秋•临颍县期末)实践与探索
如图1,边长为a的大正方形有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示).
(1)上述操作能验证的等式是 A ;(请选择正确的一个)
A.a2﹣b2=(a+b)(a﹣b)
B.a2﹣2ab+b2=(a﹣b)2
C.a2+ab=a(a+b)
(2)请应用这个公式完成下列各题:
①已知4a2﹣b2=24,2a+b=6,则2a﹣b= 4 .
②计算:1002﹣992+982﹣972+…+42﹣32+22﹣12.
【解答】解:(1)图1中阴影部分的面积为两个正方形的面积差,即a2﹣b2,
图2中的阴影部分是长为(a+b),宽为(a﹣b)的长方形,因此面积为(a+b)(a﹣b),
所以有a2﹣b2=(a+b)(a﹣b),
故答案为:A;
(2)①∵4a2﹣b2=24,
∴(2a+b)(2a﹣b)=24,
又∵2a+b=6,
∴6(2a﹣b)=24,
即2a﹣b=4,
故答案为:4;
②∵1002﹣992=(100+99)(100﹣99)=100+99,
982﹣972=(98+97)(98﹣97)=98+97,
…
22﹣12=(2+1)(2﹣1)=2+1,
∴原式=100+99+98+97+…+4+3+2+1=5050.
23.(2023秋•佛山期末)已知∠AOB=90°,直线CD与OA交于点C,与OB交于点D,点C,D均不与点O重合,CE平分∠DCO,DE平分∠CDO.
(1)如图1,当∠OCD=40°时,求∠CED的度数;
(2)如图2,延长CE与BO交于点F,过E作射线EG与CD交于点G,且满足∠CFO﹣∠GED=45°.求证:GE∥DO;
(3)如图3,过点C作CM⊥CN,MN是∠COD的外角平分线所在直线,与射线CE交于点N,与CM交于点M.在△CMN中,如果有一个角的度数是另一个角的3倍,请直接写出∠CDE的度数.
【解答】(1)解:∵∠OCD=40°,∠AOB=90°,
∴∠CDO=50°,
∵CE平分∠DCO,DE平分∠CDO,
∴∠DCE=∠OCE=∠DCO,∠CDE=∠ODE=∠CDO,
∴∠DCE=20°,∠CDE=25°,
∴∠CED=180°﹣∠DCE﹣∠CDE=135°;
(2)证明:∵CE平分∠DCO,DE平分∠CDO,
∴∠DCE=∠OCE=∠DCO,∠CDE=∠ODE=∠CDO,
∴∠CED=180°﹣∠DCE﹣∠CDE
=180°﹣(∠DCO+∠CDO)
=180°﹣(180°﹣∠O)
=180°﹣90°+∠O
=90°+45°
=135°.
∵∠CED=∠CFD+∠EDF,∠CFD=180°﹣∠CFO,
∴∠CED=180°﹣∠CFO+∠EDF,
∵∠CFO﹣∠GED=45°,
∴∠CFO=∠GED+45°,
∴∠CED=180°﹣(∠GED+45°)+∠EDF,
∴135°=∠180°﹣∠GED﹣45°+∠EDF,
∴∠GED=∠EDF,
∴GE∥DO;
(3)解:①当∠MCN=3∠N时,
∵CM⊥CN,
∴∠MCN=90°,
∴∠N=∠MCN=30°,
∴∠M=60°.
∵∠COD=90°,
∴∠DON=45°,
∴∠COM=45°.
∴∠MCO=180°﹣∠M﹣∠COM=75°.
∴∠NCO=90°﹣∠MCO=15°.
∵CE平分∠DCO,
∴∠DCO=2∠NCO=30°,
∴∠CDO=90°﹣∠DCO=60°,
∵DE平分∠CDO,
∴∠CDE=∠CDO=30°;
②当∠M=3∠N时,
∵CM⊥CN,
∴∠MCN=90°,
∴∠M+∠N=90°,
∴∠N=22.5°,∠M=67.5°,
∵∠COD=90°,
∴∠DON=45°,
∴∠COM=45°.
∴∠MCO=180°﹣∠M﹣∠COM=67.5°.
∴∠NCO=90°﹣∠MCO=22.5°.
∵CE平分∠DCO,
∴∠DCO=2∠NCO=45°,
∴∠CDO=90°﹣∠DCO=45°,
∵DE平分∠CDO,
∴∠CDE=∠CDO=22.5°.
综上,在△CMN中,如果有一个角的度数是另一个角的3倍,∠CDE的度数为30°或22.5°.
我们把如图1所示的四边形称为凸四边形,它的内角和为360°,把如图2所示的五边形称为凸五边形,它的内角和为540°.我们把如图3所示的四边形称为凹四边形,它的内角和是360°吗?答案是肯定的.它的证明方法和证明凸四边形的内角和为360°的方法相同.证明方法如下:如图3,连接AC.∵∠BAC+∠B+∠ACB=180°,…,
我们把如图1所示的四边形称为凸四边形,它的内角和为360°,把如图2所示的五边形称为凸五边形,它的内角和为540°.我们把如图3所示的四边形称为凹四边形,它的内角和是360°吗?答案是肯定的.它的证明方法和证明凸四边形的内角和为360°的方法相同.证明方法如下:如图3,连接AC.∵∠BAC+∠B+∠ACB=180°,…,
相关试卷
这是一份2024-2025学年苏科版数学七年级上册 期末真题重组卷(模拟练习),共19页。
这是一份期末真题重组卷(模拟练习)-2024-2025学年苏科版数学九年级上册,共19页。试卷主要包含了mm等内容,欢迎下载使用。
这是一份2024-2025学年人教版数学九年级上册期末模拟练习 (真题重组卷)-,共25页。









