初中数学浙教版（2024）八年级下册2.3 一元二次方程的应用完美版教学课件ppt

这是一份初中数学浙教版（2024）八年级下册2.3 一元二次方程的应用完美版教学课件ppt，共30页。PPT课件主要包含了教学目标，复习回顾，例题精讲，课堂练习，课堂总结，作业布置，你还有其它方法吗，基本相同，利润问题，二次增长后终止量为等内容，欢迎下载使用。
一元二次方程的应用是“浙教版八年级数学（下）”第二章第三节第一课时的内容。本节课的主要内容是通过具体问题情境,让学生经历一元二次方程的实际应用,体验一元二次方程的应用价值，要求学生会列一元二次方程解应用题.一元二次方程是对一元一次方程知识的延续和深化，是今后继续学习方程的重要基础，一元二次方程是初中数学中最重要的数学模型之一，与图形的面积、物体的运动、量的平均变化率等都有着密切的联系,在日常生活和生产实践中有着许多应用，一元二次方程的应用的学习有助于提高学生的抽象能力、推理能力和运算能力，在教材中有着重要的地位。
1.经历一元二次方程的实际应用,体验一元二次方程的应用价值.2.会列一元二次方程解应用题.3.提高分析问题、解决问题的能力及运算能力.
用公式法解一元二次方程的基本步骤是什么？
回忆：列方程解应用题的一般步骤是什么？
1.审：理解题意，明确已知量和未知量。2.设：设未知数3.找：理解题目中已知量、未知量及所求问题之间的相互关系，找出等量关系4.列：列出方程5.解：解方程，求出未知数的值6.验：检验方程的解能否保证实际问题有意义7.答：写出答语
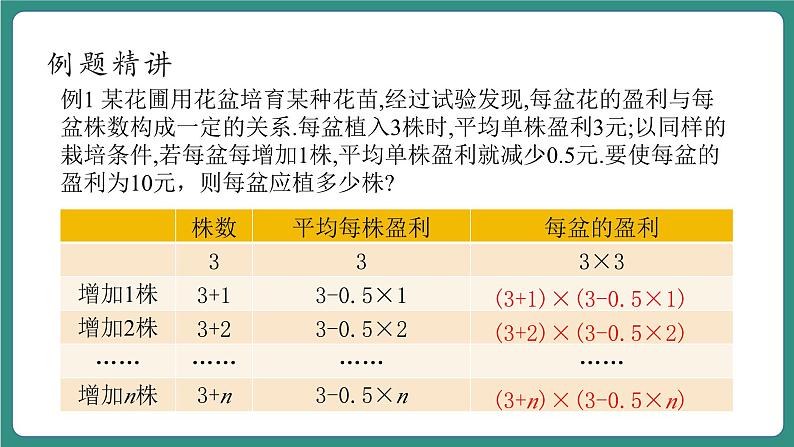
例1 某花圃用花盆培育某种花苗,经过试验发现,每盆花的盈利与每盆株数构成一定的关系.每盆植入3株时,平均单株盈利3元;以同样的栽培条件,若每盆每增加1株,平均单株盈利就减少0.5元.要使每盆的盈利为10元，则每盆应植多少株?
思考：题中的已知量是什么？未知量是什么？
已知量：每盆植入3株时,平均单株盈利3元 每盆每增加1株,平均单株盈利就减少0.5元
未知量：每盆应植多少株能够使每盆的盈利为10元
(3+1)×(3-0.5×1)
(3+2)×(3-0.5×2)
(3+n)×(3-0.5×n)
思考：题中的数量关系是什么？
主要数量关系:平均单株盈利×株数=每盆盈利;平均单株盈利=3-0.5×每盆增加的株数.
解：设每盆花苗增加x株,则每盆花苗有(3+x)株，平均单株盈利为(3-0.5x)元.由题意,得(x+3)(3-0.5x)=10.化简、整理,得x2- 3x+2=0.解这个方程,得x1 =1, x2 =2.经检验, x1 =1, x2 =2都是方程的解,且符合题意.答:要使每盆的盈利为10元，则每盆应植入4株或5株.
解：设每盆应植x株,则每盆增加的株数有(x-3)株，平均单株盈利为[3-0.5 (x-3)]元.由题意,得x [3-0.5 (x-3)]=10.化简、整理,得x2-9x+20=0.解这个方程,得x1 =4, x2 =5.经检验, x1 =4, x2 =5都是方程的解,且符合题意.答:要使每盆的盈利为10元，则每盆应植入4株或5株.
思考：列一元二次方程解应用题的基本步骤与列一元一次方程解应用题相同吗?列一元二次方程解应用题时,你认为有哪些地方更需引起注意?
1.审：理解题意，明确已知量和未知量。2.设：设未知数3.找：理解题目中已知量、未知量及所求问题之间的相互关系，找出等量关系4.列：列出方程5.解：解方程，求出未知数的值6.验：注意检验方程的两个根是否都能保证实际问题有意义7.答：写出答语
总利润=总售价-总成本=单件利润×销售数量
利润=售价-进价=进价×利润率
售价=进价×（1+利润率）
平均增长(降低)率问题：
设a为起始量，x为增长率，一次增长后，终止量为a(1+x)
设a为起始量，x为降低率，一次降低后，终止量为a(1-x)
依此类推，n次增长后，终止量为
依此类推，n次降低后，终止量为
根据统计图,求从2018年到2020年,中欧班列开行列数的平均年增长率(精确到0.1% ).
1.小明在暑假帮某服装店卖T恤衫时发现，在一段时间内，T恤衫按每件80元销售时，每天的销售量是20件，单价每降低4元，每天就可以多售出8件．已知该T恤衫的进价是每件40元．请问：当每件T恤衫降价多少元时，服装店卖该T恤衫一天能盈利1200元？设每件T恤衫降价x元，则所列方程正确的是( )A. (80－x)(20＋x)＝1200B. (80－x)(20＋2x)＝1200C. (40－x)(20＋x)＝1200D. (40－x)(20＋2x)＝1200
2.已知两个连续正奇数的积是63 ,利用一元二次 方程求这两个数.
解：设两个连续奇数为n,n+2,则由题意，得n(n+2)=63,解得n=7或n= -9(不合题意,舍去).答:两个连续正奇数是7和9.
3.某校坚持对学生进行近视眼的防治，近视学生人数逐年减少.据统 计,今年的近视学生人数是前年近视学生人数的75% ,那么这两年平均每年近视学生人数降低的百分率是多少(精确到1%)?
1.某地区2017年年底有贫困人口9万人，通过社会各界的努力，2019年年底贫困人口减少至1万人．设2017年年底至2019年年底该地区贫困人口的年平均下降率为x，则由题意可列方程为( )A. 9(1－2x)＝1 B. 9(1－x)2＝1C. 9(1＋2x)＝1 D. 9(1＋x)2＝1　　
2.一个两位数，个位上的数字比十位上的数字小4，且个位数字与十位数字的平方和比这个两位数小4，设个位数字为x，则方程为（ ）A. x2+(x-4)2=10(x-4)+x-4B. x2+(x+4)2=10x+x+4-4C. x2+(x+4)2=10(x+4)+x-4D. x2+(x-4)2=10x+(x-4)-4
3.某超市销售一种饮料,平均每天可售出100箱,每箱利润120元.为了扩大销售,增加利润,超市准备适当降价.据测算,每箱每降价1元，平均每天可多售出20箱.若要使每天销售饮料获利14000元,则每箱应降价多少元?
解：设每箱应降价x元，则由题意,得( 100+2x )( 120-x )=14000,解得x1=20, x2=50.答:每箱降价20元或50元,都能获14 000元.
一般步骤：1.审：理解题意，明确已知量和未知量。2.设：设未知数3.找：理解题目中已知量、未知量及所求问题之间的相互关系，找出等量关系4.列：列出方程5.解：解方程，求出未知数的值6.验：注意检验方程的两个根是否都能保证实际问题有意义7.答：写出答语
列一元二次方程解应用题的一般步骤是什么？
1.某公司去年4月的营业额为2500万元，按计划第二季度的总营业额要达到9100万元，设该公司5，6两月的营业额的月平均增长率为x，则由题意可列方程为( )A. 2500(1＋x)2＝9100　　B. 2500(1＋x%)2＝9100　　C. 2500(1＋x)＋2500(1＋x)2＝9100D. 2500＋2500(1＋x)＋2500(1＋x)2＝9100
2.甲、乙、丙三家超市为了促销一种定价均为m元的商品，甲超市连续两次降价20%，乙超市一次性降价40%，丙超市第一次降价30%，第二次降价10%，此时顾客要购买这种商品最划算应到( )A．甲超市 B．乙超市C．丙超市 D．乙超市或丙超市
3.为迎接马拉松赛，某市政府加大了绿化的力度，从2月份开始到4月份，绿化面积增加了44%，则平均每个月的增长率为________ .4.某体育局要组织一次排球比赛，赛制为单循环形式(每两队之间都赛一场)，计划安排28场比赛，则应邀请____支球队参加比赛．
商场某种商品平均每天可销售30件，每件盈利50元，为了尽快减少库存，商场决定采取适当的降价措施．经调査发现，每件商品每降价1元，商场平均每天可多售出2件．(1)若某天该商品每件降价3元，则当天可获利多少元？(2)设每件商品降价x元，则商场日销售量增加______件，每件商品盈利________元(用含x的代数式表示)．(3)在上述销售正常的情况下，每件商品降价多少元时，商场日盈利可达到2000元？
解： (1)(50－3)×(30＋2×3)＝1692(元)．答：当天可获利1692元．
商场某种商品平均每天可销售30件，每件盈利50元，为了尽快减少库存，商场决定采取适当的降价措施．经调査发现，每件商品每降价1元，商场平均每天可多售出2件．(2)设每件商品降价x元，则商场日销售量增加______件，每件商品盈利________元(用含x的代数式表示)．(3)在上述销售正常的情况下，每件商品降价多少元时，商场日盈利可达到2000元？
解： (3)由题意，得(50－x)×(30＋2x)＝2000.整理，得x2－35x＋250＝0，解得x1＝10，x2＝25.∵商场要尽快减少库存，∴x＝25.答：每件商品降价25元时，商场日盈利可达到2000元．