初中数学浙教版（2024）八年级下册第二章 一元二次方程2.3 一元二次方程的应用一等奖教学课件ppt

一元二次方程的应用是“浙教版八年级数学（下）”第二章第三节第二课时的内容.本节课的主要内容是继续探索一元二次方程的实际应用,进一步体验列一元二次方程解应用题的应用价值，要求学生进一步掌握列一元二次方程解应用题的方法和技能.一元二次方程是对一元一次方程知识的延续和深化，是今后继续学习方程的重要基础，一元二次方程是初中数学中最重要的数学模型之一，与图形的面积、物体的运动、量的平均变化率等都有着密切的联系,在日常生活和生产实践中有着许多应用，一元二次方程的应用的学习有助于提高学生的抽象能力、推理能力和运算能力，在教材中有着重要的地位.
1.继续探索一元二次方程的实际应用,进一步体验列一元二次方程解应用题的应用价值.2.进一步掌握列一元二次方程解应用题的方法和技能.3.提高分析问题、解决问题的能力及运算能力.
一般步骤：1.审：理解题意，明确已知量和未知量。2.设：设未知数3.找：理解题目中已知量、未知量及所求问题之间的相互关系，找出等量关系4.列：列出方程5.解：解方程，求出未知数的值6.验：注意检验方程的两个根是否都能保证实际问题有意义7.答：写出答语
列一元二次方程解应用题的一般步骤是什么？
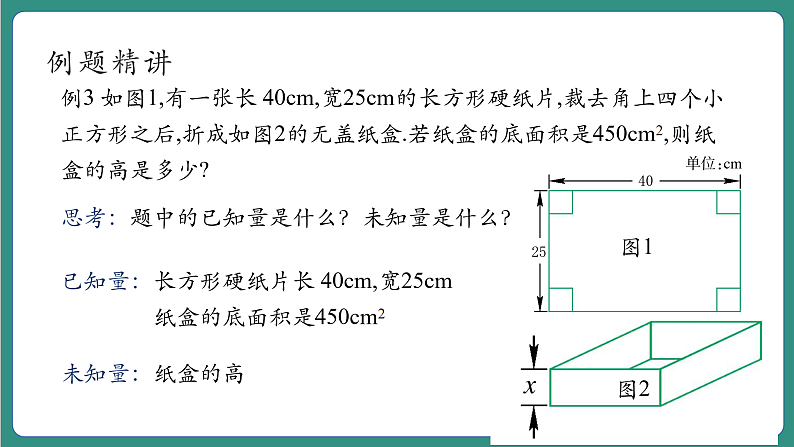
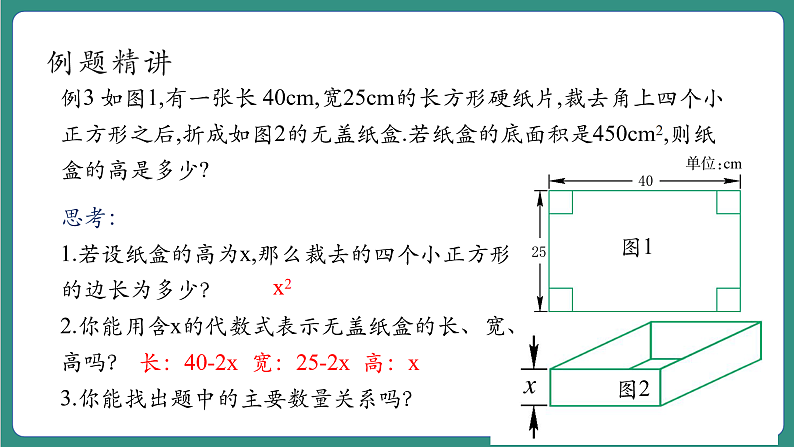
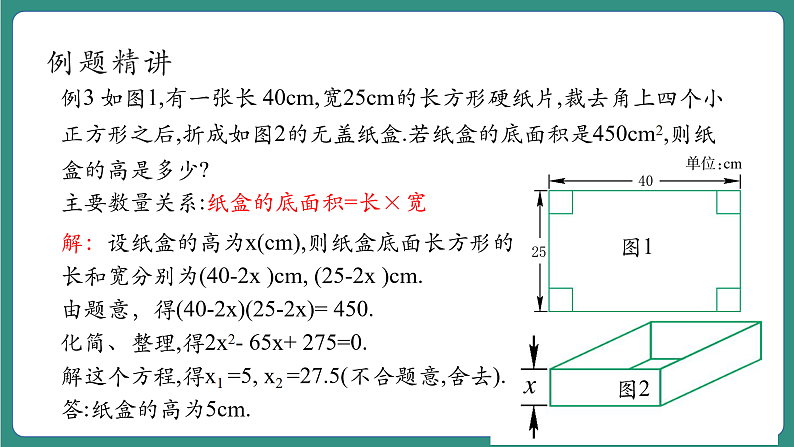
例3 如图1,有一张长 40cm,宽25cm的长方形硬纸片,裁去角上四个小正方形之后,折成如图2的无盖纸盒.若纸盒的底面积是450cm2,则纸盒的高是多少?
思考：题中的已知量是什么？未知量是什么？
已知量：长方形硬纸片长 40cm,宽25cm 纸盒的底面积是450cm2
思考：1.若设纸盒的高为x,那么裁去的四个小正方形的边长为多少？2.你能用含x的代数式表示无盖纸盒的长、宽、高吗？3.你能找出题中的主要数量关系吗？
长：40-2x 宽：25-2x 高：x
主要数量关系:纸盒的底面积=长×宽
解：设纸盒的高为x(cm),则纸盒底面长方形的长和宽分别为(40-2x )cm, (25-2x )cm.由题意，得(40-2x)(25-2x)= 450.化简、整理,得2x2- 65x+ 275=0.解这个方程,得x1 =5, x2 =27.5(不合题意,舍去).答:纸盒的高为5cm.
利用一元二次方程解决几何图形问题的方法几何图形问题，一般是从面积(或体积)等方面找相等关系，规则的几何图形直接利用面积(或体积)公式列方程即可，不规则图形一般先分割或组合成规则图形，再运用规则图形的面积(或体积)公式列方程.
一轮船(C)以30km/h的速度由西向东航行,在途中接到台风警报,台风中心(B)正以20km/h的速度由南向北移动.已知距台风中心200 km的区域(包括边界)都属于受台风影响区.当轮船接到台风警报时，测得BC=500 km, BA= 300 km.
(1)如果轮船不改变航向，轮船会不会进入台风影响区?你采用什么方法来判断? (2)如果你认为轮船会进入台风影响区,那么从接到警报开始,经多少时间就进入台风影响区?
思考：假设经t小时后，轮船和台风中心分别在C1,B1的位置，你能求出AC1,AB1的距离吗？
∵ BC=500 km, BA= 300 km∴由勾股定理可得AC=400km经过t小时后∵CC1=30t km,BB1=20t km∴ AC1=(400-30t)km,AB1=(300-20t)km
合作交流：1.运用数形结合的方法寻找相等关系,并列出方程;2.完成大题，通过相互交流,检查列方程、计算等过程是否正确;
相等关系： AC12+AB1 2 = B1C12
(400-30t)2+(300-20t)2=2002
思考：如果把航速改为10 km/h,结果将怎样?
解：若将船速改为10 km/h,则令(400-10t)2+(300-20t)2=2002化简得t2-40t+420=0.因为402-4×1×420<0,所以方程无实数根，所以船不会进入台风影响区.
利用一元二次方程解决动点问题在解决动点问题时，应先分析点的运动过程、画出代表图形和临界图形， 然后设出未知数,并用含未知数的式子表示出相关的线段的长度，再根据题目中的等量关系列方程求解.
1.某中学准备建一个面积为375 m2的矩形游泳池，且游泳池的宽比长短10 m．设游泳池的长为x m，则可列方程为( )A．x(x－10)＝375 B．x(x＋10)＝375C．2x(2x－10)＝375 D．2x(2x＋10)＝375
3.如图，在△ABC中，∠ABC＝90°，AB＝8cm，BC＝6cm，动点P，Q分别从点A，B同时开始移动（移动方向如图所示），点P的速度为1cm/s，点Q的速度为2cm/s，点Q移动到点C后停止，点P也随之停止运动，若使△PBQ的面积为15cm2，则点P运动的时间是( )A．2sB．3sC．4sD．5s
1.如图，在长为100米，宽为80米的矩形场地上修建两条宽度相等且互相垂直的道路，剩余部分进行绿化，要使绿化面积为7644平方米，则道路的宽应为多少米？设道路的宽为x米，则可列方程为( )A．100×80－100x－80x＝7644B．(100－x)(80－x)＋x2＝7644C．(100－x)(80－x)＝7644D．100x＋80x＝356
3.如图，在矩形ABCD中，AB＝6cm，BC＝12cm，点P从点A沿边AB向点B以1cm/s的速度移动；同时，点Q从点B沿边BC向点C以2cm/s的速度移动，设运动的时间为t秒，有一点到终点运动即停止，当t＝______时，S△DPQ＝28cm2．
如图，有一段15m米长的旧围墙AB，现打算利用该围墙的一部分(或全部)为一边，再用32m长的篱笆围成一块长方形场地CDEF.(1)怎样围成一个面积为126m2的长方形场地？(2)长方形场地面积能达到130m2吗？如果能，请给出设计方案，如果不能，请说明理由.
解：(1)设CD=xm，则DE=(32-2x)m，依题意得x(32-2x)=126，整理得x2-16x+63=0，解得x1=9，x2=7，当x1=9时，32-2x=14，当x2=7时，32-2x=18＞15（不合题意，舍去），∴能围成一个长14m，宽9m的长方形场地.
如图，有一段15m米长的旧围墙AB，现打算利用该围墙的一部分(或全部)为一边，再用32m长的篱笆围成一块长方形场地CDEF.(2)长方形场地面积能达到130m2吗？如果能，请给出设计方案，如果不能，请说明理由.
解：(2)设CD=ym，则DE=(32-2y)m，依题意得y(32-2y)=130，整理得y2-16y+65=0， =(-16)2-4×1×65=-4＜0，故方程没有实数根，∴长方形场地面积不能达到130m2.
利用一元二次方程解决几何图形问题的方法是什么？几何图形问题，一般是从面积(或体积)等方面找相等关系，规则的几何图形直接利用面积(或体积)公式列方程即可，不规则图形一般先分割或组合成规则图形，再运用规则图形的面积(或体积)公式列方程.如何利用一元二次方程解决动点问题？在解决动点问题时，应先分析点的运动过程、画出代表图形和临界图形， 然后设出未知数,并用含未知数的式子表示出相关的线段的长度，再根据题目中的等量关系列方程求解.
1.如图，在长为70 m，宽为40 m的长方形花园中，欲修宽度相等的观赏路(阴影部分所示)，要使观赏路面积占总面积的，则路宽x应满足的方程是( )A．(40－x)(70－x)＝2450B．(40－x)(70－x)＝350C．(40－2x)(70－3x)＝2450D．(40－2x)(70－3x)＝350
2.以正方形木板的边长为长，在正方形木板上锯掉一块2 cm宽的长方形木条，剩下部分的面积是48 cm2，那么原正方形木板的面积是( )A．8 cm2 B．8 cm2或64 cm2 C．64 cm2 D．36 cm2
3.如图，在Rt△ACB中，∠C＝90°，AC＝30 cm，BC＝25 cm.动点P从点C出发，沿CA方向运动，速度是2 cm/s；动点Q从点B出发，沿BC方向运动，速度是1 cm/s，则经过____s后，P，Q两点之间相距25 cm.
在矩形ABCD中，AB=6cm，BC=12cm，点P从点A沿边AB向点B以1cm/s的速度移动；同时点Q从点B沿边BC向点C以2cm/s的速度移动，设运动时间为t.（1）问几秒后△PBQ的面积等于8cm2？（2）是否存在t，使△PDQ的面积等于26cm2？
在矩形ABCD中，AB=6cm，BC=12cm，点P从点A沿边AB向点B以1cm/s的速度移动；同时点Q从点B沿边BC向点C以2cm/s的速度移动，设运动时间为t.（2）是否存在t，使△PDQ的面积等于26cm2？
解：(2)假设存在t使得△PDQ面积为26cm2，则72-6t-t(6-t)-3(12-2t)=26,整理得,t2-6t+10=0，∵ =36-4×1×10=-4＜0，∴原方程无解,所以不存在t,能够使△PDQ的面积等于26cm2.