浙教版（2024）八年级下册4.1 多边形完美版教学ppt课件

这是一份浙教版（2024）八年级下册4.1 多边形完美版教学ppt课件，共30页。PPT课件主要包含了教学目标，复习导入，探究新知，课堂练习，课堂总结，作业布置，知识技能类作业，必做题，选做题，综合实践类作业等内容，欢迎下载使用。
《4.1.1多边形》是“浙教版八年级数学（下）”第四章第一节第一课时的内容.本节课的主要内容是了解多边形的相关概念，带领学生经历四边形内角和定理的发现过程,要求学生理解四边形内角和定理的证明，会用四边形内角和定理解决简单的图形问题.多边形在日常生活中有着广泛的应用，能为今后学习“图形与几何”的知识打下坚实基础，有利于培养学生数形结合的思想，在教材中有着非常重要的地位和作用.
1.了解多边形的概念2.经历四边形内角和定理的发现过程.3.理解四边形内角和定理的证明.4.会用四边形内角和定理解决简单的图形问题.5.体验把四边形问题转化为三角形问题来解决的化归思想.6.提高分析问题、解决问题的能力，增强数学应用意识7.在空间观念的基础上进一步建立几何直观，提升抽象能力和推理能力.
你能说出三角形的定义吗？
在同一平面内，由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
你能类比三角形的定义给出四边形的定义吗？
在同一平面内，由任意两条都不在同一条直线上的四条线段首尾顺次相接所组成的图形叫做四边形.
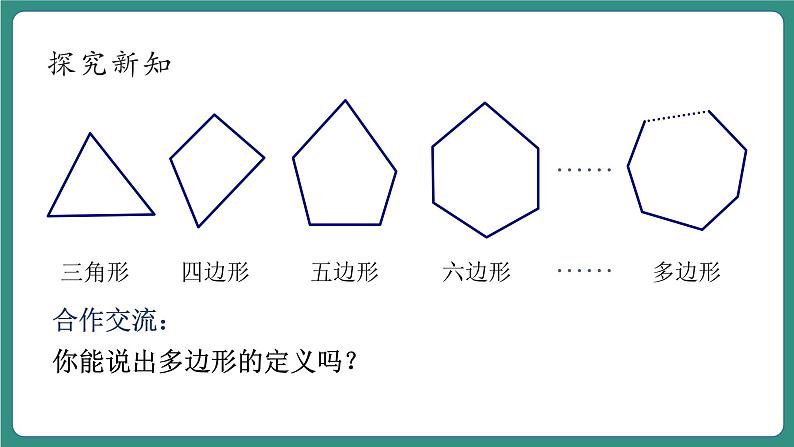
合作交流：你能说出多边形的定义吗？
在同一平面内，由不在同一条直线上的若干条线段(线段的条数不小于3)首尾顺次相接形成的图形叫做多边形.组成多边形的各条线段叫做多边形的边.
边数为3的多边形叫三角形,边数为4的多边形叫四边形.类似地,边数为5的多边形叫五边形……边数为n的多边形叫n边形(n为正整数,且n≥3).
多边形相邻两边组成的角叫做多边形的内角.多边形一边的延长线与相邻的另一边所组成的角叫做多边形的外角.多边形每一个内角的顶点叫做多边形的顶点.
连结多边形不相邻两个顶点的线段叫做多边形的对角线.
说一说：说出如图所示的四边形ABCD的各条边和各个内角,并画出各条对角线和任意一个外角.
边：AB,BC,CD,DA内角：∠A,∠B,∠C,∠D
思考：n边形的对角线的条数为多少？
合作学习：在纸上任意画一个四边形,剪下它的四个角,把它们拼在一起(四个角的顶点重合).你发现了什么?其他同学与你的发现相同吗?你能把你的发现概括成一个命题吗?你能证明这个命题吗?
四边形的内角和等于360°.
已知:四边形ABCD.求证:∠A+∠B+∠C+∠D= 360°.
证明：如图 ,连结BD.∵∠A+∠ABD+∠ADB=180°，∠C+∠CBD+∠CDB= 180°,∴∠A+∠ABD+∠ADB+∠C+∠CBD+∠CDB = 180°+180°= 360°,即∠A+∠ABC+∠C+∠CDA = 360°.
例1 如图,四边形风筝的四个内角∠A,∠B,∠C, ∠D的度数之比为1:1:0.6:1. 求它的四个内角的度数.
解：∵∠A+∠B+∠C+∠D=360° (四边形的内角和等于360°),又∵∠A,∠B,∠C,∠D的度数之比为1:1:0.6:1, 设∠A=x度,则有x+x+0.6x+x= 360,解得x= 100.∴∠A=∠B=∠D=100°,∠C= 100°×0.6= 60°.
1.下列图形中,不是多边形的是(　　)
2.一块四边形ABCD玻璃被打破,如图所示.小红想购买一块一模一样的玻璃,经测量,∠A=120°,∠B=60°,∠C=150°,则∠D的度数为(　　)A.65°　B.45°　C.30°　D.20°
3.如果过某多边形的一个顶点的对角线有5条,则该多边形是(　　)A.九边形　　　　B.八边形C.七边形　　　　D.六边形
1.在四边形ABCD中,∠A∶∠B∶∠C∶∠D=1∶2∶1∶2,则∠D=(　　)A.150°　B.120°　C.90°　D.60°
2.在四边形ABCD中,∠A+∠C=180°,∠B比∠D大60°,则∠B的度数为(　　)A.60°　　　　B.80°　　　　C.120°　　　　D.130°
3.在四边形ABCD中,设∠A=∠B=∠C=α,∠D=β,则下列说法正确的是(　　)A.若α=60°,则β=60°　　　　B.若α=70°,则β=70°C.若α=80°,则β=80°　　　　D.若α=90°,则β=90°
1.如图,∠ABE是四边形ABCD的一个外角,已知∠ABE=∠D.求证:∠A+∠C=180°.
解：∵∠ABE=∠D,∠ABE+∠ABC=180°,∴∠ABC+∠D=180°,又∵四边形内角和等于360°,∴∠A+∠C=180°.
n边形的对角线的条数为多少？
四边形的内角和为多少？
1.在四边形ABCD中，已知∠A与∠B互补，∠D＝70°，则∠C的度数为( )70° B. 90°C. 110° D. 140°
2.在四边形ABCD中，AD∥BC，则它的四个内角之比∠A:∠B:∠C:∠D可能是( )3∶4∶8∶9 B. 8∶3∶4∶9　　　C. 9∶3∶4∶8 D. 9∶4∶8∶3
3.如图，在四边形ABCD中，∠A＋∠D＝240°，∠B＝3α，∠C＝α2－5α，则α的度数为_____．4.如图,在四边形ABCD中,DA⊥AB,∠C=100°,∠D=110°,则∠B的度数为_____.
1.如图，在四边形ABCD中，∠B＝∠D＝90°，∠A∶∠C＝1∶5，AB＝6，CD＝3.求：(1)∠A，∠C的度数．(2)AD，BC的长度．(3)四边形ABCD的面积．
解： (1) ∵四边形ABCD的内角和为360°，∠B＝∠D＝90°，∴∠A＋∠C＝180°.∵∠A∶∠C＝1∶5，∴∠A＝30°，∠C＝150°.
1.如图，在四边形ABCD中，∠B＝∠D＝90°，∠A∶∠C＝1∶5，AB＝6，CD＝3.求：(2)AD，BC的长度．
1.如图，在四边形ABCD中，∠B＝∠D＝90°，∠A∶∠C＝1∶5，AB＝6，CD＝3.求：(3)四边形ABCD的面积．