初中数学浙教版（2024）八年级下册第四章 平行四边形4.2 平行四边形一等奖教学ppt课件

这是一份初中数学浙教版（2024）八年级下册第四章 平行四边形4.2 平行四边形一等奖教学ppt课件，共30页。PPT课件主要包含了教学目标，复习导入，探究新知，课堂练习，课堂总结，作业布置，知识技能类作业，必做题，选做题，综合实践类作业等内容，欢迎下载使用。
《4.2.1平行四边形及其性质》是“浙教版八年级数学（下）”第四章第二节第一课时的内容.本节课的主要内容是了解平行四边形的概念，带领学生探索平行四边形的性质：平行四边形的对角相等、平行四边形的对边相等、不稳定性，要求学生理解并能应用这些性质.平行四边形是一种十分重要的平面图形,它具有三角形不能概括的许多性质,因此平行四边形是几何学中一个重要的基础图形，平行四边形及其性质的学习有助于学生在空间观念的基础上进一步建立几何直观，提升抽象能力和推理能力，在教材中有着重要的地位.
1.了解平行四边形的概念.会用符号表示平行四边形.2.理解“平行四边形的对角相等”的性质,并能应用这个性质.3.理解“平行四边形的对边相等”的性质,并能应用这个性质.4.了解平行四边形的不稳定性及其实际应用.5.提高分析问题、解决问题的能力，增强数学应用意识6.在空间观念的基础上进一步建立几何直观，提升抽象能力和推理能力.
四边形的内角和为多少？
四边形的内角和等于360°.
多边形的内角和定理是什么？
n边形的内角和为(n-2)×180°(n≥3).
多边形的外角和定理是什么？
任何多边形的外角和为360°.
你知道遮阳篷的伸缩架为什么采用平行四边形的结构吗？
与三角形的稳定性相反,四边形具有不稳定性的特点.如图,这三个平行四边形的边长都对应相等,但它们的形状却不相同.
平行四边形的不稳定性在日常生活和生产实际中有许多应用，如衣帽架、伸缩门、可伸缩的遮阳篷等,都反映了四边形的不稳定性的应用.
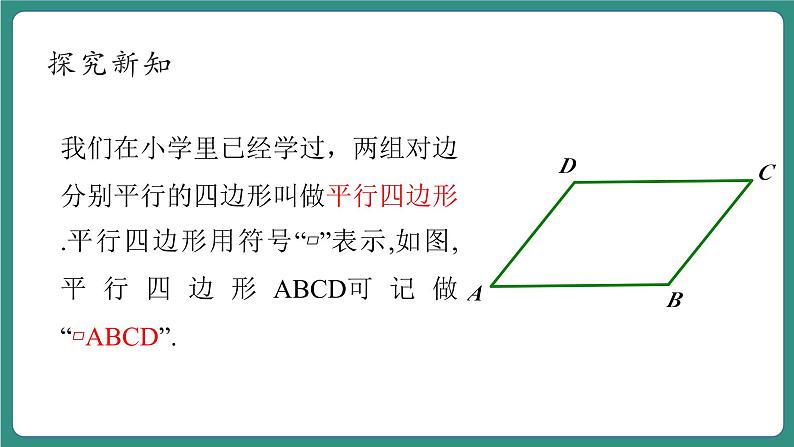
我们在小学里已经学过，两组对边分别平行的四边形叫做平行四边形.平行四边形用符号“▱”表示,如图,平行四边形ABCD可记做“▱ABCD”.
合作学习：用两块相同的三角板拼一个平行四边形.讨论下面的问题:(1)怎样拼能拼出一个平行四边形?你能拼出多少个形状不同的平行四边形?(2)怎样证明你拼出的四边形是平行四边形?(3)通过上述活动,你发现平行四边形有哪些性质?你能证明这些 性质吗?
合作学习：用两块相同的三角板拼一个平行四边形.讨论下面的问题:(1)怎样拼能拼出一个平行四边形?你能拼出多少个形状不同的平行四边形?
(2)怎样证明你拼出的四边形是平行四边形?
以右图为例.证明：∵四边形ABCD是用两块相同的三角板拼成的∴∠1=∠2,∠3=∠4∴AB∥CD，AD∥BC∴四边形ABCD是平行四边形
(3)通过上述活动,你发现平行四边形有哪些性质?你能证明这些性质吗?
平行四边形有以下性质定理:平行四边形的对角相等.平行四边形的对边相等.
已知:四边形ABCD是平行四边形.求证:∠A=∠C,∠ABC=∠CDA;AB=CD,BC= DA.
证明：连结BD.在四边形ABCD中,AB//CD(平行四边形的定义),∴∠ABD=∠CDB.同理，∠ADB=∠CBD.又∵BD=DB,∴△ABD≌△CDB.∴AB=CD, BC=DA,∠A=∠C.同理可得，∠ABC=∠CDA.
例1 已知:如图, E, F分别是▱ABCD的边AD,BC上的点,且 AF// CE.求证:DE= BF,∠BAF=∠DCE.
解：如图,在▱ABCD中,AD// BC, AD=CB (平行四边形的对边相等).∵AF// CE,∴四边形AFCE是平行四边形(平行四边形的定义).∴AE=CF (平行四边形的对边相等).
续：∵AD=CB,∴AD- AE=CB-CF,即DE= BF.∵∠BAD=∠DCB,∠EAF=∠FCE (平行四边形的对角相等),∴∠BAD-∠EAF=∠DCB-∠FCE,即∠BAF=∠DCE.
1.如图,在▱ABCD中,∠A+∠C=80°,则∠D=(　　)A.80°　B.40°　C.70°　D.140°
2.在▱ABCD中,AD=3,AB=2,则▱ABCD的周长为(　　)A.9　　　　 B.10　　　　 C.11　 　　　D.12
3.如图,直线a∥b,点A、D在直线a上,点B在直线b上,点C为直线b上一动点,则当∠BCD=　　　　时,四边形ABCD是平行四边形. 
1.如图,在平行四边形ABCD中,CE⊥AB,E为垂足,如果∠D=60°,那么∠BCE=(　　)A.30°　　　　B.40°　　　　C.60°　　　　D.120°
2.如图，在▱ABCD中，若∠B=60°，AB=5cm，则以下结论正确的是(　　)A. BC=5cm，∠D=60°B. ∠C=120°，CD=5cmC. AD=5cm，∠A=60°D. ∠A=120°，AD=5cm
3.如图,在▱ABCD中,EF∥AD,HG∥AB,则图中平行四边有　　　　个. 
1.如图,在▱ABCD中,点E,F在对角线AC上,∠CBE=∠ADF.求证:(1)AE=CF;(2)BE∥DF.
解： (2)∵△ADF≌△CBE,∴∠AFD=∠CEB,∴BE∥DF.
平行四边形有哪些性质?
1.平行四边形的对角相等.2.平行四边形的对边相等.3.平行四边形具有不稳定性.
1.如图,点A,B,C在同一直线上,点D,E,F,G在同一直线上,且AC∥DG,AD∥BE∥CF,AF∥BG,则图中平行四边形有(　　)A.4个　B.5个　C.3个　D.6个
2.如图,▱ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为(　　)A.BE=DF　　　　B.BF=DEC.AE=CF　　　　D.∠1=∠2
3.要使四边形木架(用4根木条钉成)不变形,至少需要加钉1根木条固定,要使五边形木架不变形,至少需要加钉2根木条固定,要使六边形木架不变形,至少需要加钉3根木条固定,……,那么要使一个n边形木架不变形,至少需要加钉________根木条固定. 4.如图,在▱ABCD中,DE平分∠CDA,且点E是线段BC的中点,BC=10,AE=6,则DE的长为________.
1.如图,在▱ABCD中,点E为边CD的中点,连结AE并延长交BC的延长线于点F.(1)求证:△ADE≌△FCE;(2)若AD=5,求BF的长.
证明： (2)∵四边形ABCD是平行四边形,∴AD=BC=5,∵△ADE≌△FCE,∴AD=CF=5,∴BF=BC+CF=5+5=10.