初中数学浙教版（2024）八年级下册第四章 平行四边形4.4 平行四边形的判定精品教学ppt课件

这是一份初中数学浙教版（2024）八年级下册第四章 平行四边形4.4 平行四边形的判定精品教学ppt课件，共30页。PPT课件主要包含了教学目标，复习导入，探究新知，课堂练习，课堂总结，作业布置，对角线，平行线段，两条平行线，平行线之间的距离等内容，欢迎下载使用。
《4.4.1平行四边形的判定定理》是“浙教版八年级数学（下）”第四章第四节第一课时的内容。本节课的主要内容是平行四边形的判定定理1、2。要求学生探究证明平行四边形的判定定理“一组对边平行并且相等的四边形是平行四边形”和“两组对边分别相等的四边形是平行四边形”，要求学生会用平行四边形的判定定理判断一个四边形是不是平行四边形。本节课的学习不仅是对平行四边形定义和性质的深化拓展，还为后续的矩形、菱形、正方形等知识的学习奠定了理论基础，在教材中有着重要的地位。
1.掌握平行四边形的判定定理“一组对边平行并且相等的四边形是平行四边形”.2.掌握平行四边形的判定定理“两组对边分别相等的四边形是平行四边形”.3.会用平行四边形的判定定理,判断一个四边形是不是平行四边形.4.经历得到和验证数学结论的过程，增强几何直观，提升证明推理能力.
平行四边形的性质:平行四边形的对边　　　 　. 平行四边形的对角　 　　　.平行四边形的　 　　　互相平分.夹在两条平行线间的　 　　　相等.夹在　 　　　间的垂线段相等.两条平行线中，一条直线上的点到另一条直线的距离,叫做这两条　 　 　　.平行四边形是　 　对称图形,　 　　　是它的对称中心.
合作交流：命题“平行四边形的一组对边平行且相等”是真命题吗?写出它的逆命题.这个逆命题是真命题吗?
∵两组对边分别平行的四边形叫做平行四边形又∵平行四边形的对边相等∴命题“平行四边形的一组对边平行且相等”是真命题它的逆命题为一组对边平行并且相等的四边形是平行四边形
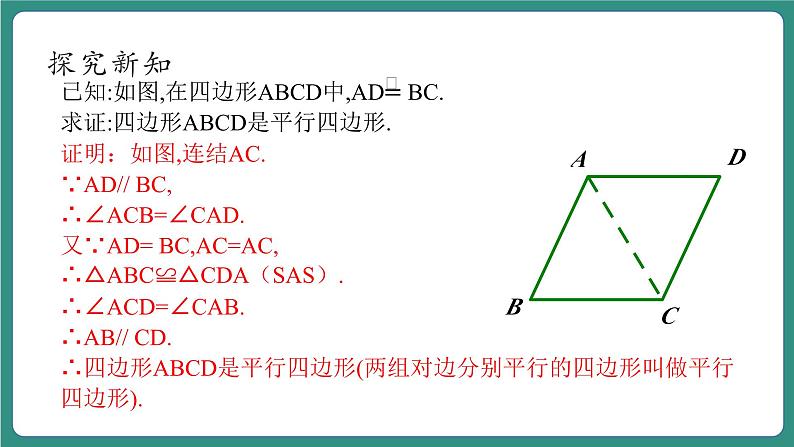
分析：因为 AD// BC,根据平行四边形的定义,只要再证明AB//DC即可.而要证明AB//DC,可连结AC,证明相应的内错角相等.
证明：如图,连结AC.∵AD// BC,∴∠ACB=∠CAD.又∵AD= BC,AC=AC,∴△ABC≌△CDA（SAS）.∴∠ACD=∠CAB.∴AB// CD.∴四边形ABCD是平行四边形(两组对边分别平行的四边形叫做平行四边形).
平行四边形的判定定理1：一组对边平行并且相等的四边形是平行四边形.
我们还有以下判定一个四边形是平行四边形的定理:两组对边分别相等的四边形是平行四边形.你能完成这一定理的证明吗？
已知:在四边形ABCD中,AB=DC,AD=BC.求证:四边形ABCD是平行四边形.
分析：因为 AD=BC,根据平行四边形的判定定理1,只要再证明AD//BC即可.而要证明AD//BC,可连结AC,证明相应的内错角相等.
证明：如图,连结AC.∵ AB=DC,BC=AD,AC=AC,∴△ABC≌△CDA（SSS）.∴∠DAC=∠BCA.∴ AD//BC.∴四边形ABCD是平行四边形(一组对边平行并且相等的四边形是平行四边形).
平行四边形的判定定理2：两组对边分别相等的四边形是平行四边形.
几何语言：∵AB=DC,AD=BC∴四边形ABCD是平行四边形
例1 已知:如图,在▱ABCD中,E,F分别是AB, CD的中点.求证:EF//AD.
证明：在▱ABCD中，∵AB CD(平行四边形的一组对边平行且相等).又∵E,F分别是AB,CD的中点，∴AE DF.∴四边形AEFD是平行四边形(一组对边平行并且相等的四边形是平行四边形).∴EF//AD(平行四边形的定义).
1.如图,在四边形ABCD中,AB∥CD,要使四边形ABCD是平行四边形,下列可添加的条件不正确的是(　　)A.AD=BC B.AB=CD C.AD∥BC D.∠A=∠C
2.在下列条件中，不能确定四边形ABCD为平行四边形的是(　　)A. ∠A=∠C，∠B=∠DB. ∠A=∠B=∠C=90°C. ∠A+∠B=180°，∠B+∠C=180°D. ∠A+∠B=180°，∠C+∠D=180°
3.已知四边形ABCD，有以下四个条件：①AB∥CD；②AB=CD；③BC∥AD；④BC=AD. 从这四个条件中任选两个，能判定四边形ABCD为平行四边形的选法共有(　　)A. 6种 B. 5种 C. 4种 D. 3种
1.将两个各边都不相等的全等三角形按不同的方式拼成四边形，其中平行四边形有(　　)A． 1个 B． 2个 C． 3个 D． 4个
2.如图,以线段AB的端点B为顶点作一个锐角∠ABC,点D为射线BC上任意一点,过点D作DF∥AB,在射线DF上截取DE=AB,连结AE,则四边形ABDE是　　 　　,依据:　　　 　　　　　　　　　.　　　 　　　　　　　　　
一组对边平行并且相等的四边形
　　 　　
　　　　　　　　　　　　.
3.如图,在四边形ABCD中,AB=CD,AD=BC,对角线AC、BD相交于点O,若AC=6,则线段OA的长度等于　　　　　　　.
如图,在四边形ABCD中,∠B=∠C,E是边BC上一点,连结DE,AB=DE,DE=DC.求证:四边形ABED是平行四边形.
证明:∵DE=DC,∴∠DEC=∠C,∵∠B=∠C,∴∠B=∠DEC,∴AB∥DE,∵AB=DE,∴四边形ABED是平行四边形.
如何判定一个四边形是平行四边形？
定义：两组对边分别平行的四边形叫做平行四边形.平行四边形的判定定理1：一组对边平行并且相等的四边形是平行四边形.平行四边形的判定定理2：两组对边分别相等的四边形是平行四边形.
1.我们称四个顶点都恰好在格点的平行四边形为格点平行四边形,如图,A,B为4×4的正方形网格中的两个格点,则以A,B为顶点的格点平行四边形的个数是(　　)A.10　　　　B.11　　　　C.12　　　　D.13
2.如图，在四边形ABCD中，BD⊥AD，BD⊥BC，AD=11-x，BC=x-5．当x=________ 时，四边形ABCD是平行四边形．
3.如图,将直角三角形ABC沿射线BC方向平移6 cm,得到三角形A'B'C',已知∠ACB=90°,BC=3 cm,AC=4 cm,则阴影部分的面积为　　　　cm2. 
如图,在四边形ABCD中,AD∥BC,延长BC到点E,使CE=BC,连结AE交CD于点F,点F是CD的中点.求证:(1)△ADF≌△ECF;(2)四边形ABCD是平行四边形.
(2)证明：∵△ADF≌△ECF,∴AD=EC,∵CE=BC,∴AD=BC,∵AD∥BC,∴四边形ABCD是平行四边形.