广东省深圳市福田外国语学校（东校区） 2024-2025学年七年级上学期期中数学试卷

这是一份广东省深圳市福田外国语学校（东校区） 2024-2025学年七年级上学期期中数学试卷，共18页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．（3分）“鸣语既过渐细微，映空摇飏如丝飞”是唐代诗人杜甫作品《雨不绝》中的诗句，意为喧哗的雨已经过去，逐渐变得细微，映着天空摇漾如丝的细雨飘飞．诗中描写雨滴下来形成雨丝，用数学语言解释这一现象为（ ）
A．点动成线B．线动成面
C．面动成体D．面面相交成线
2．（3分）七年级以“福外鸣天精神”为主题开展入学教育，激励学生爱校拼搏，奋发有为．如图是一个正方体的平面展开图，则原正方体中与“鸣”字所在面相对的面上标有的字是（ ）
A．福B．精C．神D．外
3．（3分）文化和旅游部10月8日公布2024年国庆节假期文化和旅游市场情况．经文化和旅游部数据中心测算，全国国内出游7.65亿人次．7.65亿用科学记数法表示是（ ）
A．76.5×107B．7.65×108C．0.765×109D．7.65×109
4．（3分）a、b两数在数轴上位置如图所示，将a、b、﹣a、﹣b用“＜”连接，其中正确的是（ ）
A．a＜﹣a＜b＜﹣bB．﹣b＜a＜﹣a＜bC．﹣a＜b＜﹣b＜aD．﹣b＜a＜b＜﹣a
5．（3分）下列计算正确的是（ ）
A．x2y﹣2x2y＝﹣x2yB．2（a+2b）＝2a+2b
C．7ab﹣（﹣3ab）＝10D．a﹣（b﹣c）＝a﹣b﹣c
6．（3分）按如图所示的运算程序，当输入x的值为1时，输出y的值为（ ）
A．﹣1B．﹣4C．9D．11
7．（3分）规定一种新运算：a⊗b＝a2﹣2b，则2⊗[1⊗（﹣2）]的值是（ ）
A．6B．﹣2C．﹣6D．10
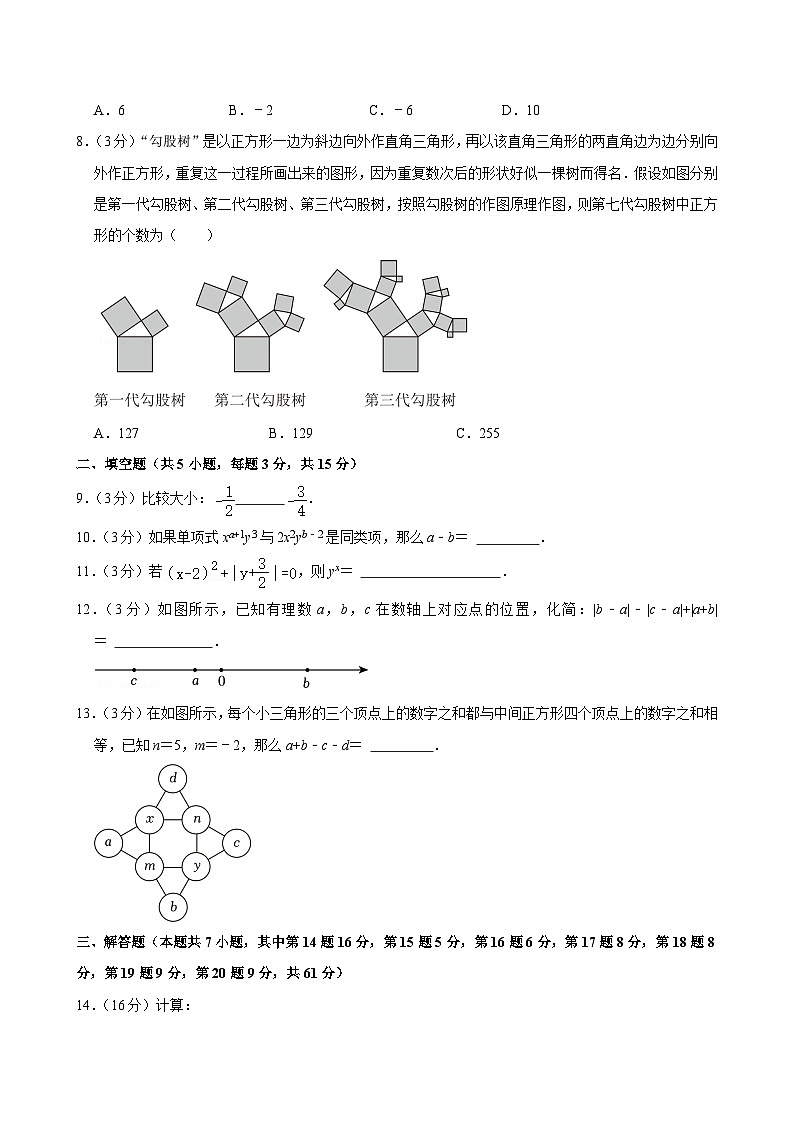
8．（3分）“勾股树”是以正方形一边为斜边向外作直角三角形，再以该直角三角形的两直角边为边分别向外作正方形，重复这一过程所画出来的图形，因为重复数次后的形状好似一棵树而得名．假设如图分别是第一代勾股树、第二代勾股树、第三代勾股树，按照勾股树的作图原理作图，则第七代勾股树中正方形的个数为（ ）
A．127B．129C．255
二、填空题（共5小题，每题3分，共15分）
9．（3分）比较大小： ．
10．（3分）如果单项式xa+1y3与2x2yb﹣2是同类项，那么a﹣b＝ ．
11．（3分）若，则yx＝ ．
12．（3分）如图所示，已知有理数a，b，c在数轴上对应点的位置，化简：|b﹣a|﹣|c﹣a|+|a+b|＝ ．
13．（3分）在如图所示，每个小三角形的三个顶点上的数字之和都与中间正方形四个顶点上的数字之和相等，已知n＝5，m＝﹣2，那么a+b﹣c﹣d＝ ．
三、解答题（本题共7小题，其中第14题16分，第15题5分，第16题6分，第17题8分，第18题8分，第19题9分，第20题9分，共61分）
14．（16分）计算：
（1）（﹣40）﹣28﹣（﹣19）+（﹣24）；
（2）；
（3）；
（4）﹣22×（﹣9）+16÷（﹣2）3﹣|﹣4×5|．
15．（5分）先化简，再求值：，其中x＝﹣1，y＝﹣2．
16．（6分）如图，是由7个大小相同的小立方体块搭建的几何体，其中每个小正方体的棱长为1厘米．请按要求在方格内分别画出从这个几何体的三个不同方向看到的形状图．
17．（8分）某小区的一块长方形绿地的造型如图所示（单位：m），其中两个扇形表示绿地，两块绿地用五彩石隔开．
（1）绿地的面积为 平方米；（用含有a，b，π的式子表示）
（2）若b＝a，
①若铺设五彩石费用为每平方米160元，种草的费用为每平方米80元，则美化这块长方形区域共需多少元？（用含有a，π的式子表示）
②若要求绿地面积大于这块地总面积的，试问该设计方案是否合乎要求？请说明理由．
18．（8分）某电器商销售一种微波炉和一种电磁炉，微波炉每台定价800元，电磁炉每台定价200元．商场周年庆时决定开展促销活动，活动期间向顾客提供两种优惠方案．
方案一：买1台微波炉送1台电磁炉；
方案二：微波炉和电磁炉都按定价的九折付款．
现某顾客要向该电器商购买微波炉10台，电磁炉x台（x＞10）．
（1）如果该顾客按方案一购买，那么需付款 元；如果该顾客按方案二购买，那么需付款 元．（用含x的式子表示）
（2）如果x＝30，若只选择一种方案，请通过计算说明此时按哪种方案购买较为划算．
（3）当x＝30时，若可以通过多种方案购买，你能给出一种更为省钱的方案吗？试写出你的购买方法，并计算需付款多少元．
19．（9分）“整体思想”是中学数学解题中的一种重要思想方法，它在多项式的化简与求值中的应用极为广泛．
例：当多项式x2+3x+5的值为7时，求多项式3x2+9x﹣2的值．
解：因为x2+3x+5＝7，所以x2+3x＝2．
所以3x2+9x﹣2＝3（x2+3x）﹣2＝3×2﹣2＝4．
请根据阅读材料，解决下列问题：
（1）把（x﹣y）2看成一个整体，化简3（x﹣y）2﹣7（x﹣y）2+2（x﹣y）2的结果是 ；
（2）已知x2+3x﹣2＝0．求x2（5x2+15x）+30x﹣2044的值；
（3）《九章算术》是中国古典数学著作，其中有一个问题：“今有上禾三秉，中禾二秉，下禾一秉，实三十九斗．上禾二秉，中禾三秉，下禾一秉，实三十四斗；上禾一秉，中禾二秉，下禾三秉，实二十六斗，问上、中、下禾实一秉各几何．”原文意思为：优质稻子3捆，普通稻子2捆，劣质稻子1捆，能碾39斗米；优质稻子2捆，普通稻子3捆，劣质稻子1捆，能碾34斗米；优质稻子1捆，普通稻子2捆，劣质稻子3捆能碾26斗米．我们假设优质稻子每捆能碾米a斗，普通稻子每捆能碾米b斗，劣质稻子每捆能碾米c斗．请你运用“整体思想”，求出优质稻子13捆，普通稻子9捆，劣质稻子2捆，共能碾多少斗米？
20．（9分）类比同类项的概念，我们规定：所含字母相同，并且相同字母的指数之差的绝对值都小于或等于1的项是“准同类项”．
例如：a3b4与2a4b3是“准同类项”．
（1）给出下列四个单项式：
①5a4b5；②﹣3a2b5；③；④
其中与a4b5是“准同类项”的是 （填写序号）
（2）已知A、B、C均为关于a，b的多项式A＝a4b5+3a3b4+（n﹣2）a2b3，B＝2a2b3﹣3a2bn+a4b5，C＝A﹣B．若C的任意两项都是“准同类项”，求n的值．
（3）已知D，E均为关于a，b的单项式，D＝5a2bm，E＝3anb4，其中m＝|x﹣2|+k，n＝3k，若D，E是“准同类项”，求出①x的最大值是 ；②x的最小值是 ．
2024-2025学年广东省深圳市福田外国语学校（东校区）七年级（上）期中数学试卷
参考答案与试题解析
一、选择题（共8小题，每题3分，共24分，每题有四个选项，其中只有一个是正确的）
1．（3分）“鸣语既过渐细微，映空摇飏如丝飞”是唐代诗人杜甫作品《雨不绝》中的诗句，意为喧哗的雨已经过去，逐渐变得细微，映着天空摇漾如丝的细雨飘飞．诗中描写雨滴下来形成雨丝，用数学语言解释这一现象为（ ）
A．点动成线B．线动成面
C．面动成体D．面面相交成线
【考点】点、线、面、体．
【答案】A
【分析】根据点动成线分析即可．
【解答】解：根据题意可知，雨滴滴下来形成雨丝属于点动成线．
故选：A．
2．（3分）七年级以“福外鸣天精神”为主题开展入学教育，激励学生爱校拼搏，奋发有为．如图是一个正方体的平面展开图，则原正方体中与“鸣”字所在面相对的面上标有的字是（ ）
A．福B．精C．神D．外
【考点】专题：正方体相对两个面上的文字．
【答案】B
【分析】根据正方体表面展开图的“相间、Z端是对面”进行判断即可．
【解答】解：由正方体表面展开图的“相间、Z端是对面”可知，
“鸣”与“精”是对面，
故选：B．
3．（3分）文化和旅游部10月8日公布2024年国庆节假期文化和旅游市场情况．经文化和旅游部数据中心测算，全国国内出游7.65亿人次．7.65亿用科学记数法表示是（ ）
A．76.5×107B．7.65×108C．0.765×109D．7.65×109
【考点】科学记数法—表示较大的数．
【答案】B．
【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正数；当原数的绝对值＜1时，n是负数．
【解答】解：7.65亿＝765000000＝7.65×108．
故选：B．
4．（3分）a、b两数在数轴上位置如图所示，将a、b、﹣a、﹣b用“＜”连接，其中正确的是（ ）
A．a＜﹣a＜b＜﹣bB．﹣b＜a＜﹣a＜bC．﹣a＜b＜﹣b＜aD．﹣b＜a＜b＜﹣a
【考点】有理数大小比较；数轴．
【答案】B
【分析】根据a、b两数在数轴上的位置和相反数的定义在数轴上标出表示﹣a，﹣b的点，利用数轴进行比较即可．
【解答】解：由题意作图如下：
由图象可得：﹣b＜a＜﹣a＜b，
故选：B．
5．（3分）下列计算正确的是（ ）
A．x2y﹣2x2y＝﹣x2yB．2（a+2b）＝2a+2b
C．7ab﹣（﹣3ab）＝10D．a﹣（b﹣c）＝a﹣b﹣c
【考点】整式的加减．
【答案】A
【分析】根据相关法则进行计算即可得到答案．
【解答】解：A．x2y﹣2x2y＝﹣x2y，故选选项正确，符合题意；
B．2（a+2b）＝2a+4b，故选选项错误，不符合题意；
C．7ab﹣（﹣3ab）＝10ab，故选选项错误，不符合题意；
D．a﹣（b﹣c）＝a﹣b+c，故选选项错误，不符合题意；
故选：A．
6．（3分）按如图所示的运算程序，当输入x的值为1时，输出y的值为（ ）
A．﹣1B．﹣4C．9D．11
【考点】代数式求值；有理数的混合运算．
【答案】D
【分析】先把x＝1代入y＝x2﹣5中求出y的值，若y的值大于等于0，则输出y的值，否则把y的值重新赋值给x再代入y＝x2﹣5中计算，如此反复，直到计算出的y值大于等于0后输出即可．
【解答】解：当输入x＝1时，
y＝12﹣5＝﹣4＜0，此时y＜0，
还需输入x＝﹣4时，
y＝（﹣4）2﹣5＝16﹣5＝11＞0，
∴输出y的值为11．
故选：D．
7．（3分）规定一种新运算：a⊗b＝a2﹣2b，则2⊗[1⊗（﹣2）]的值是（ ）
A．6B．﹣2C．﹣6D．10
【考点】有理数的混合运算．
【答案】C
【分析】根据题中的新定义化简所求式子，计算即可得到结果．
【解答】解：∵a⊗b＝a2﹣2b，
∴2⊗[1⊗（﹣2）]
＝2⊗[12﹣2×（﹣2）]
＝2⊗（1+4）
＝2⊗5
＝22﹣2×5
＝4﹣10
＝﹣6，
故选：C．
8．（3分）“勾股树”是以正方形一边为斜边向外作直角三角形，再以该直角三角形的两直角边为边分别向外作正方形，重复这一过程所画出来的图形，因为重复数次后的形状好似一棵树而得名．假设如图分别是第一代勾股树、第二代勾股树、第三代勾股树，按照勾股树的作图原理作图，则第七代勾股树中正方形的个数为（ ）
A．127B．129C．255
【考点】规律型：图形的变化类．
【答案】C
【分析】由特殊情况总结出一般规律，即可得到答案．
【解答】解：第一代勾股树中正方形的个数：1+2＝3（个），
第二代勾股树中正方形的个数：1+2+22＝7（个），
第三代勾股树中正方形的个数：1+2+22+23＝15（个），
……，
第七代勾股树中正方形的个数：1+2+22+……+27＝255（个）．
故选：C．
二、填空题（共5小题，每题3分，共15分）
9．（3分）比较大小： ＞ ．
【考点】有理数大小比较．
【答案】见试题解答内容
【分析】根据两个负数比较大小，绝对值大的反而小．
【解答】解：∵|﹣|＝＝．|﹣|＝，
∵＜，
∴﹣＞﹣，
故答案为＞．
10．（3分）如果单项式xa+1y3与2x2yb﹣2是同类项，那么a﹣b＝ ﹣4 ．
【考点】同类项．
【答案】﹣4．
【分析】根据同类项的定义列出方程，再求解即可．
【解答】解：由同类项的定义可知a+1＝2，b﹣2＝3，
解得a＝1，b＝5，
∴a﹣b＝1﹣5＝﹣4．
故答案为：﹣4．
11．（3分）若，则yx＝ ．
【考点】非负数的性质：偶次方；非负数的性质：绝对值；有理数的乘方．
【答案】．
【分析】根据非负数的性质列出方程求出未知数的值，再代入所求代数式计算即可．
【解答】解：∵，
∴x﹣2＝0，＝0，
∴x＝2，y＝，
∴yx＝＝．
故答案为：．
12．（3分）如图所示，已知有理数a，b，c在数轴上对应点的位置，化简：|b﹣a|﹣|c﹣a|+|a+b|＝ ﹣a+2b+c ．
【考点】数轴；绝对值．
【答案】﹣a+2b+c．
【分析】利用数轴知识和绝对值的定义解答．
【解答】解：由数轴图可知，c＜a＜0＜b，|a|＜b，
∴b﹣a＞0，c﹣a＜0，a+b＞0，
∴|b﹣a|﹣|c﹣a|+|a+b|
＝ b﹣a﹣[﹣（c﹣a）]+a+b
＝b﹣a+c﹣a+a+b
＝﹣a+2b+c．
故答案为：﹣a+2b+c．
13．（3分）在如图所示，每个小三角形的三个顶点上的数字之和都与中间正方形四个顶点上的数字之和相等，已知n＝5，m＝﹣2，那么a+b﹣c﹣d＝ 14 ．
【考点】整式的加减．
【答案】14．
【分析】依题意得a＝y+5，b＝x+5，c＝x﹣2，d＝y﹣2，由此可得a+b﹣c﹣d的值．
【解答】解：∵n＝5，m＝﹣2，
∴中间正方形四个顶点上的数字之和为：x+y+m+n＝x+y+3，
又∵每个小三角形的三个顶点上的数字之和都与中间正方形四个顶点上的数字之和相等，
∴a+x﹣2＝x+y+3，b+y﹣2＝x+y+3，c+y+5＝x+y+3，d+x+5＝x+y+3，
∴a＝y+5，b＝x+5，c＝x﹣2，d＝y﹣2，
∴a+b﹣c﹣d＝y+5+x+5﹣（x﹣2）﹣（y﹣2）＝y+5+x+5﹣x+2﹣y+2＝14．
故答案为：14．
三、解答题（本题共7小题，其中第14题16分，第15题5分，第16题6分，第17题8分，第18题8分，第19题9分，第20题9分，共61分）
14．（16分）计算：
（1）（﹣40）﹣28﹣（﹣19）+（﹣24）；
（2）；
（3）；
（4）﹣22×（﹣9）+16÷（﹣2）3﹣|﹣4×5|．
【考点】有理数的混合运算．
【答案】（1）﹣73；
（2）﹣36；
（3）﹣2；
（4）14．
【分析】（1）利用有理数的加减法则计算即可；
（2）利用有理数的乘除法则计算即可；
（3）利用乘法分配律计算即可；
（4）先算乘方及绝对值，再算乘除，最后算加减即可．
【解答】解：（1）原式＝﹣68+19﹣24
＝﹣49﹣24
＝﹣73；
（2）原式＝﹣4×（﹣3）×（﹣3）
＝﹣36；
（3）原式＝﹣×（﹣36）﹣×（﹣36）+×（﹣36）
＝3+1﹣6
＝﹣2；
（4）原式＝﹣4×（﹣9）+16÷（﹣8）﹣20
＝36﹣2﹣20
＝14．
15．（5分）先化简，再求值：，其中x＝﹣1，y＝﹣2．
【考点】整式的混合运算—化简求值．
【答案】见试题解答内容
【分析】利用整式的相应的法则对式子进行化简，再代入相应的值运算即可．
【解答】解：
＝10x2﹣6y2﹣3xy+5y2﹣10x2
＝﹣y2﹣3xy，
当x＝﹣1，y＝﹣2时，
原式＝﹣（﹣2）2﹣3×（﹣1）×（﹣2）
＝﹣4﹣6
＝﹣10．
16．（6分）如图，是由7个大小相同的小立方体块搭建的几何体，其中每个小正方体的棱长为1厘米．请按要求在方格内分别画出从这个几何体的三个不同方向看到的形状图．
【考点】作图﹣三视图．
【答案】见解析．
【分析】根据观察物体的方法，分别明确从正面、左面和上面看到的形状，解答即可．
【解答】解：三视图如图所示：
17．（8分）某小区的一块长方形绿地的造型如图所示（单位：m），其中两个扇形表示绿地，两块绿地用五彩石隔开．
（1）绿地的面积为 π（a2+b2） 平方米；（用含有a，b，π的式子表示）
（2）若b＝a，
①若铺设五彩石费用为每平方米160元，种草的费用为每平方米80元，则美化这块长方形区域共需多少元？（用含有a，π的式子表示）
②若要求绿地面积大于这块地总面积的，试问该设计方案是否合乎要求？请说明理由．
【考点】列代数式．
【答案】（1）π（a2+b2）；
（2）①（240a2﹣25πa2）元；
②该设计方案合乎要求，理由见解答．
【分析】（1）将两个扇形的面积相加，即可用含有a，b，π的式子表示出绿地的面积；
（2）代入b＝a，用含有a，π的式子表示出绿地的面积．
①利用美化这块长方形区域所需费用＝铺设每平方米五彩石所需费用×（这块地的总面积﹣绿地的面积）+种每平方米草所需费用×绿地面积，即可用含有a，π的式子表示出美化这块长方形区域所需费用；
②求出这块地总面积的，将其与绿地面积比较后，即可得出结论．
【解答】解：（1）根据题意得：绿地的面积为πa2+πb2＝π（a2+b2）（平方米）．
故答案为：π（a2+b2）；
（2）当b＝a时，π（a2+b2）
＝π[a2+（a）2]
＝πa2．
①根据题意得：160[（a+a）a﹣πa2]+80×πa2
＝160（a2﹣πa2）+80×πa2
＝160×a2﹣160×πa2+80×πa2
＝240a2﹣50πa2+25πa2
＝（240a2﹣25πa2）（元），
∴美化这块长方形区域共需（240a2﹣25πa2）元；
②该设计方案合乎要求，理由如下：
这块地总面积的是（a+a）a＝a2＝0.9a2（平方米）．
∵πa2≈0.95a2＞0.9a2，
∴该设计方案合乎要求．
18．（8分）某电器商销售一种微波炉和一种电磁炉，微波炉每台定价800元，电磁炉每台定价200元．商场周年庆时决定开展促销活动，活动期间向顾客提供两种优惠方案．
方案一：买1台微波炉送1台电磁炉；
方案二：微波炉和电磁炉都按定价的九折付款．
现某顾客要向该电器商购买微波炉10台，电磁炉x台（x＞10）．
（1）如果该顾客按方案一购买，那么需付款 （200x+6000） 元；如果该顾客按方案二购买，那么需付款 （180x+7200） 元．（用含x的式子表示）
（2）如果x＝30，若只选择一种方案，请通过计算说明此时按哪种方案购买较为划算．
（3）当x＝30时，若可以通过多种方案购买，你能给出一种更为省钱的方案吗？试写出你的购买方法，并计算需付款多少元．
【考点】代数式求值；列代数式．
【答案】（1）（200x+6000）；（180x+7200）；
（2）按方案一购买较合算；
（3）先按方案一购买10台微波炉，送10台电磁炉，再按方案二购买20台电磁炉，共需付款11600元．
【分析】（1）根据“方案一”的要求可知买10台微波炉，送10台电磁炉，用10台微波炉的金额加上（x﹣10）台电磁炉的金额即可；
根据“方案二”求出“优惠”后的单价，再根据单价×数量＝总价进行计算即可；
（2）把x＝30分别代入两个代数式，求出相应的代数式的值，比较得出答案；
（3）先按方案一购买10台微波炉，送10台电磁炉，再按方案二购买20台电磁炉．
【解答】解：（1）若该客户按方案一购买，需付款800×10+（x﹣10）×200＝（200x+6000）元，
若该客户按方案二购买，需付款（800×10+200x）×90%＝（180x+7200）元；
故答案为：（200x+6000）；（180x+7200）；
（2）当x＝30时，方案一；200×30+6000＝12000（元）；
方案二：180×30+7200＝12600（元），
因为12000＜12600，
所以按方案一购买较合算．
（3）最省钱的购买方案为：先按方案一购买10台微波炉，送10台电磁炉，再按方案二购买20台电磁炉，共需付款10×800+200×20×90%＝11600（元）．
19．（9分）“整体思想”是中学数学解题中的一种重要思想方法，它在多项式的化简与求值中的应用极为广泛．
例：当多项式x2+3x+5的值为7时，求多项式3x2+9x﹣2的值．
解：因为x2+3x+5＝7，所以x2+3x＝2．
所以3x2+9x﹣2＝3（x2+3x）﹣2＝3×2﹣2＝4．
请根据阅读材料，解决下列问题：
（1）把（x﹣y）2看成一个整体，化简3（x﹣y）2﹣7（x﹣y）2+2（x﹣y）2的结果是 ﹣2（x﹣y）2 ；
（2）已知x2+3x﹣2＝0．求x2（5x2+15x）+30x﹣2044的值；
（3）《九章算术》是中国古典数学著作，其中有一个问题：“今有上禾三秉，中禾二秉，下禾一秉，实三十九斗．上禾二秉，中禾三秉，下禾一秉，实三十四斗；上禾一秉，中禾二秉，下禾三秉，实二十六斗，问上、中、下禾实一秉各几何．”原文意思为：优质稻子3捆，普通稻子2捆，劣质稻子1捆，能碾39斗米；优质稻子2捆，普通稻子3捆，劣质稻子1捆，能碾34斗米；优质稻子1捆，普通稻子2捆，劣质稻子3捆能碾26斗米．我们假设优质稻子每捆能碾米a斗，普通稻子每捆能碾米b斗，劣质稻子每捆能碾米c斗．请你运用“整体思想”，求出优质稻子13捆，普通稻子9捆，劣质稻子2捆，共能碾多少斗米？
【考点】解三元一次方程组；代数式求值．
【答案】（1）﹣2（x﹣y）2；
（2）﹣2004；
（3）164斗米．
【分析】（1）把（x﹣y）2看成一个整体，合并同类项即可；
（2）由已知等式求出x2+3x的值，原式变形后整体代入计算即可求出值；
（3）根据题意列出三元一次方程组，利用整体代入法求出优质稻子13捆，普通稻子9捆，劣质稻子2捆，共能碾的米即可．
【解答】解：（1）3（x﹣y）2﹣7（x﹣y）2+2（x﹣y）2
＝（3﹣7+2）（x﹣y）2
＝﹣2（x﹣y）2；
故答案为：﹣2（x﹣y）2；
（2）因为x2+3x﹣2＝0，
所以x2+3x＝2，
x2（5x2+15x）+30x﹣2044
＝x2×5×（x2+3x）+30x﹣2044
＝x2×5×2+30x﹣2044
＝10x2+30x﹣2024
＝10（x2+3x）﹣2024
＝10×2﹣2024
＝﹣2004；
（3）根据题意得：
①×4+②﹣③得：13a+9b+2c＝39×4+34﹣26＝164，
则优质稻子13捆，普通稻子9捆，劣质稻子2捆，共能碾164斗米．
20．（9分）类比同类项的概念，我们规定：所含字母相同，并且相同字母的指数之差的绝对值都小于或等于1的项是“准同类项”．
例如：a3b4与2a4b3是“准同类项”．
（1）给出下列四个单项式：
①5a4b5；②﹣3a2b5；③；④
其中与a4b5是“准同类项”的是 ①③ （填写序号）
（2）已知A、B、C均为关于a，b的多项式A＝a4b5+3a3b4+（n﹣2）a2b3，B＝2a2b3﹣3a2bn+a4b5，C＝A﹣B．若C的任意两项都是“准同类项”，求n的值．
（3）已知D，E均为关于a，b的单项式，D＝5a2bm，E＝3anb4，其中m＝|x﹣2|+k，n＝3k，若D，E是“准同类项”，求出①x的最大值是 6 ；②x的最小值是 ﹣ ．
【考点】整式的加减；绝对值；同类项．
【答案】（1）①③；
（2）3或4；
（3）6，﹣．
【分析】（1）根据准同类项的定义进行验证即可；
（2）根据C＝A﹣B进行计算，再根据定义计算即可；
（3）根据D与E是“准同类项”，得到m＝5或3或4，n＝1或2或3，然后再分x≥2时或x＜2时，再根据准同类项的定义计算即可．
【解答】解：（1）根据“准同类项”得①③，
故答案为：①③．
（2）∵A＝a4b5+3a3b4+（n﹣2）a2b3，B＝2a2b3﹣3a2bn+a4b5，C＝A﹣B＝（n﹣4）a2b3+3a3b4+3a2bn，
∴n＝3或4；
（3）∵D与E是“准同类项”，
又D＝5a2bm，E＝3anb4，
∴m＝5或3或4，n＝1或2或3，
又m＝|x﹣2|+k，n＝3k，
①当x≥2时，m＝x﹣2+k，k＝，
∴x＝m+2﹣，要使x最大，m＝5，n＝1，
∴x最大＝5+2﹣＝6．
要使x最小，
若m＝3，n＝3，得x＝3+2﹣1＝4．
∴x的最大值为6，最小值为4．
②当x＜2时，n＝﹣k，
m＝2﹣x+k，k＝，
∴x＝2+﹣m，
当m＝5，n＝1时，x取最小值，为﹣，
当m＝3，n＝3时，x取最大值，为2+1﹣3＝0；
综上所述，x的最大值为6，最小值为﹣；
声明：试题解析著作权属所有，未经书面同意，不得复制发布日期：2024/11/24 1:03:23；用户：13551613617；邮箱：13551613617；学号：60190894