广东省佛山市禅城区华英学校2024—2025学年上学期期中考试八年级数学试卷

这是一份广东省佛山市禅城区华英学校2024—2025学年上学期期中考试八年级数学试卷，共31页。试卷主要包含了填空题请将下列各题的正确答案，速算题，解答题等内容，欢迎下载使用。
1．（3分）下列数中是无理数的是（ ）
A．B．2πC．0.14D．
2．（3分）下列描述，能确定具体位置的是（ ）
A．祖庙附近B．教室第2排
C．北偏东55°D．东经118°，北纬40°
3．（3分）如图，在△ABC中，∠C＝90°，若AC＝1，AB＝2，则BC的长是（ ）
A．1B．C．2D．
4．（3分）在平面直角坐标系中，点（﹣7，﹣10）在（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
5．（3分）估算的值在（ ）
A．1和2之间B．2和3之间C．3和4之间D．4和5之间
6．（3分）在平面直角坐标系中，点M（4，﹣3）到x轴的距离为（ ）
A．4B．3C．﹣4D．﹣3
7．（3分）已知一次函数y＝kx+2（k≠0）的函数值y随x的增大而增大，则该函数的图象大致是（ ）
A．B．
C．D．
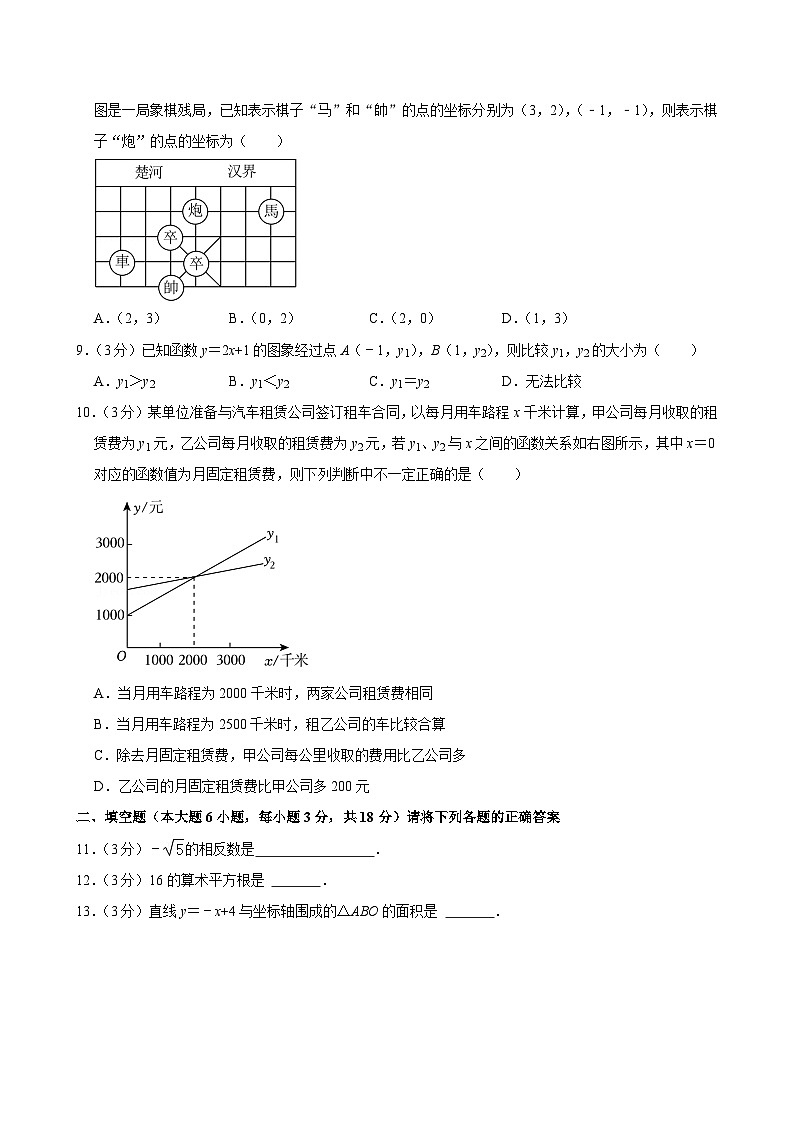
8．（3分）象棋在中国有着三千多年的历史，由于用具简单，趣味性强，成为流行极为广泛的益智游戏．如图是一局象棋残局，已知表示棋子“马”和“帥”的点的坐标分别为（3，2），（﹣1，﹣1），则表示棋子“炮”的点的坐标为（ ）
A．（2，3）B．（0，2）C．（2，0）D．（1，3）
9．（3分）已知函数y＝2x+1的图象经过点A（﹣1，y1），B（1，y2），则比较y1，y2的大小为（ ）
A．y1＞y2B．y1＜y2C．y1＝y2D．无法比较
10．（3分）某单位准备与汽车租赁公司签订租车合同，以每月用车路程x千米计算，甲公司每月收取的租赁费为y1元，乙公司每月收取的租赁费为y2元，若y1、y2与x之间的函数关系如右图所示，其中x＝0对应的函数值为月固定租赁费，则下列判断中不一定正确的是（ ）
A．当月用车路程为2000千米时，两家公司租赁费相同
B．当月用车路程为2500千米时，租乙公司的车比较合算
C．除去月固定租赁费，甲公司每公里收取的费用比乙公司多
D．乙公司的月固定租赁费比甲公司多200元
二、填空题（本大题6小题，每小题3分，共18分）请将下列各题的正确答案
11．（3分）﹣的相反数是 ．
12．（3分）16的算术平方根是 ．
13．（3分）直线y＝﹣x+4与坐标轴围成的△ABO的面积是 ．
14．（3分）如图，阴影部分是两个正方形，其它部分是两个直角三角形和一个正方形．若右边的直角三角形ABC中，AC＝17，BC＝15，则阴影部分的面积是 ．
15．（3分）已知AB∥x轴，A的坐标为（2，6），AB＝4，则点B的坐标是 ．
16．（3分）如图，教室的墙面ADEF与地面ABCD垂直，点P在墙面上．若PA＝AB＝5米，点P到AD的距离是3米，有一只蚂蚁要从点P爬到点B，它的最短行程是 米．
三、速算题（每空1分，共10分）
17．（10分）①＝ ；②＝ ；③＝ ；④＝ ；⑤＝ ；⑥＝ ；⑦＝ ；⑧＝ ；⑨＝ ；⑩＝ ．
四、解答题（18题8分，19题6分，20-22题各8分，23题、24题各12分，共62分）
18．（8分）计算：
（1）；
（2）．
19．（6分）如图，在平面直角坐标系xOy中，点A的坐标为（﹣4，4），点B的坐标为（﹣2，0），点C的坐标为（﹣1，2）．
（1）请画出△ABC关于y轴的对称图形△A1B1C1；
（2）直接写出点C1的坐标为 ；（直接写出答案）
（3）点P在y轴上，且满足△PCC1的面积为3，直接写出点P坐标为 ．（直接写出答案）
20．（8分）图1是某品牌婴儿车，图2为其简化结构示意图，现测得AB＝CD＝6dm，BC＝3dm，AD＝9dm，其中AB与BD之间由一个固定为90°的零件连接（即∠ABD＝90°），根据安全标准需满足BC⊥CD，通过计算说明该车是否符合安全标准．
21．（8分）小明制作了一张面积为256cm2的正方形贺卡想寄给朋友．现有一个长方形信封如图所示，长、宽之比为3：2，面积为420cm2．
（1）求长方形信封的长和宽；
（2）小明能将贺卡不折叠就放入此信封吗？请通过计算给出判断．
22．（8分）我国传统的计重工具﹣﹣秤的应用，方便了人们的生活．如图①，可以用秤砣到秤纽的水平距离，来得出秤钩上所挂物体的重量．称重时，若秤杆上秤砣到秤纽的水平距离为x（厘米）时，秤钩所挂物重为y（斤），则y是x的一次函数．表中为若干次称重时所记录的一些数据．
（1）在表x，y的数据中，发现有一对数据记录错误．在图②中，通过描点的方法，观察判断哪一对数据是错误的？
（2）①求出y与x之间的函数解析式；
②秤杆上秤砣到秤纽的水平距离为16厘米时，秤钩所挂物重是多少？
23．（12分）在“勾股定理”一章的学习中，我们体会到了勾股定理应用的广泛性，以及“数形结合”是解决数学问题的一种重要的思想方法．
（1）【已有认识】既可以从算术平方根的角度理解，结合勾股定理的知识，也能将其看成是直角边都为1的直角三角形的斜边长，即，由此得到在数轴上寻找所表示的点的方法，如图1．
【拓展运用】如图2，点O、点A在数轴上，且OA＝2，AB＝1，AB⊥OA于A，以点O为圆心，OB长为半径画弧，交数轴于点P，则数轴中点P表示的数是 ．（直接写出答案）
（2）【已有认识】结合正方形网格，我们还可以表示某些长度为无理数的线段．
【拓展运用】请在图3正方形网格（每个小正方形的边长为1）内画出顶点在格点的△ABC，其中，，，并求出△ABC的面积，以及点C到AB边的距离．
（3）【已有认识】如图4，结合直角坐标系，我们发现：要求出坐标系中A、B两点的距离，显然是转化为求Rt△ABC的斜边长．下面以求DE为例来说明如何解决：
从坐标系中发现：D（﹣1，﹣4），E（6，﹣2），
所以DF＝|6﹣（﹣1）|＝7，EF＝|﹣2﹣（﹣4）|＝2，
所以由勾股定理可得，．
【拓展运用】①在图5中，设A（x1，y1），B（x2，y2），AC∥y轴，BC∥x轴，AC⊥BC于点C，则AC＝ ，BC＝ ，由此得到平面直角坐标系内任意两点间的距离公式，AB＝（直接写出答案）
②图4中，平面直角坐标系中有两点M（﹣3，4），N（﹣6，1），P为x轴上任一点，则PM+PN的最小值为 ；（直接写出答案）
③应用平面内两点间的距离公式，求代数式的最小值为： .（直接写出答案）
24．（12分）【阅读材料】建系法：通过构建平面直角坐标，借助点坐标、函数等方法，可以把几何关系转化成代数关系．【初步运用】某年广东省数学中考卷的填空压轴题：如图1，边长分别为6，4，2的三个正方形拼接在一起，它们的底边在同一直线上，则图中阴影部分（直角梯形）的面积为多少？
解决这道题目方法很多，其中一种就是“建系法”，请补全以下解题思路．（直接写出答案）
解题思路：
①如图2，以直线BC为x轴，以直线AB为y轴，以点B为原点建立直角坐标系．
②由题意得，点A坐标为（0，6），点G坐标为（6，4），点F坐标为 ，点H坐标为（12，0）．
③由点A和点H的坐标求出直线AH的关系式为 ．
④因为点M的横坐标为6，且点M在直线AH上，所以代入横坐标即可求出纵坐标．
⑤同理求出点N坐标，从而得到线段GM和线段FN的长，从而求出阴影部分直角梯形的面积为 ．
【迁移探究】如图，长方形ABCD中，∠ABC＝∠BCD＝∠CDA＝∠DAB＝90°，AB＝CD＝4，AD＝BC＝6，AD∥BC，AB∥CD，点E是边AD上的一点，AE＝AB，BE交AC于点F．
（1）请用“建系法”求四边形EFCD的面积．（要求：建立直角坐标系时，把长方形的边放在坐标轴上，并把长方形置于第一象限．）
（2）在题（1）建立的直角坐标系基础下，点P是长方形AB边、AD边和CD边上的一个动点，沿着由B→A→D→C的方向移动，点Q是点P在运动过程中关于x轴的对称点．请问在点P的运动过程中，是否存在某一时刻使得△QBF是一个等腰三角形，若存在，请直接写出此时点Q的坐标；若不存在，请说明理由．
（3）在题（1）建立的直角坐标系基础下，把△ACD沿着直线AC折叠，点D的对应点为点D'，请直接写出点D′的坐标．
2024-2025学年广东省佛山市禅城区华英学校八年级（上）期中数学试卷
参考答案与试题解析
一、选择题（本大题10小题，每小题3分，共30分）在每小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑
1．（3分）下列数中是无理数的是（ ）
A．B．2πC．0.14D．
【答案】B
【分析】由于无理数就是无限不循环小数．初中范围内学习的无理数有：π，2π等；开方开不尽的数；以及0.1010010001…，等有这样规律的数．由此即可判定选择项．
【解答】解：A、因为是分数，所以是有理数，不符合题意；
B、2π是开方开不尽的数，所以2π是无理数，符合题意；
C、0.14是分数，所以是有理数，不符合题意；
D、＝2，因为2是整数，所以是有理数，不符合题意．
故选：B．
【点评】此题主要考查了无理数的定义，解题要注意带根号的数与无理数的区别：带根号的数不一定是无理数，带根号且开方开不尽的数一定是无理数．
2．（3分）下列描述，能确定具体位置的是（ ）
A．祖庙附近B．教室第2排
C．北偏东55°D．东经118°，北纬40°
【答案】D
【分析】根据坐标的定义，确定位置需要两个数据，据此对各选项分析判断利用排除法求解．
【解答】解：A．祖庙附近，不能确定具体位置，故此选项不符合题意；
B．教室第2排，不能确定具体位置，故此选项不符合题意；
C．北偏东55°，不能确定具体位置，故此选项不符合题意；
D．东经118°，北纬40°，能确定具体位置，故此选项符合题意．
故选：D．
【点评】本题考查坐标确定位置，理解确定坐标的两个数是解题的关键．
3．（3分）如图，在△ABC中，∠C＝90°，若AC＝1，AB＝2，则BC的长是（ ）
A．1B．C．2D．
【答案】B
【分析】直接根据勾股定理列式计算即可．
【解答】解：∵∠C＝90°，AC＝1，AB＝2，
∴BC＝＝＝，
即BC的长是，
故选：B．
【点评】本题考查了勾股定理，熟练掌握勾股定理是解题的关键．
4．（3分）在平面直角坐标系中，点（﹣7，﹣10）在（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
【答案】C
【分析】根据坐标符号特征与象限的关系判定即可．
【解答】解：点（﹣7，﹣10）在第三象限，
故选：C．
【点评】本题考查了点的坐标，熟练掌握各象限点的坐标特征是关键．
5．（3分）估算的值在（ ）
A．1和2之间B．2和3之间C．3和4之间D．4和5之间
【答案】D
【分析】根据算术平方根的定义估算无理数的大小即可．
【解答】解：∵42＝16，52＝25，而16＜20＜25，
∴4＜＜5，
即介在4和5之间，
故选：D．
【点评】本题考查估算无理数的大小，掌握算术平方根的定义是正确解答的前提．
6．（3分）在平面直角坐标系中，点M（4，﹣3）到x轴的距离为（ ）
A．4B．3C．﹣4D．﹣3
【答案】B
【分析】根据点到x轴的距离即为纵坐标的绝对值即可得出结果．
【解答】解：根据点的坐标的几何意义，点A（4，﹣3）到x轴的距离为纵坐标的绝对值即为3，
故选：B．
【点评】本题考查的是点的坐标的几何意义，横坐标的绝对值就是点到y轴的距离，纵坐标的绝对值就是点到x轴的距离．
7．（3分）已知一次函数y＝kx+2（k≠0）的函数值y随x的增大而增大，则该函数的图象大致是（ ）
A．B．
C．D．
【答案】A
【分析】根据一次函数的性质即可得到结论．
【解答】解：∵一次函数y＝kx+2（k≠0）的函数值y随x的增大而增大，
∴k＞0，
∴此函数的图象经过一二三象限．
故选：A．
【点评】本题考查的是一次函数的图象，一次函数的性质，熟练掌握一次函数的性质是解答此题的关键．
8．（3分）象棋在中国有着三千多年的历史，由于用具简单，趣味性强，成为流行极为广泛的益智游戏．如图是一局象棋残局，已知表示棋子“马”和“帥”的点的坐标分别为（3，2），（﹣1，﹣1），则表示棋子“炮”的点的坐标为（ ）
A．（2，3）B．（0，2）C．（2，0）D．（1，3）
【答案】B
【分析】根据表示棋子“马”和“帥”的点的坐标分别为（3，2），（﹣1，﹣1），可得到表示棋子“卒”的位置是直角坐标系的原点，继而求得棋子“炮”的点的坐标即可．
【解答】解：∵表示棋子“马”和“帥”的点的坐标分别为（3，2），（﹣1，﹣1），
∴表示棋子“卒”的位置是直角坐标系的原点，
∴表示棋子“炮”的点的坐标为（0，2）．
故选：B．
【点评】本题考查了坐标确定位置，建立坐标系找到坐标系的原点是关键．
9．（3分）已知函数y＝2x+1的图象经过点A（﹣1，y1），B（1，y2），则比较y1，y2的大小为（ ）
A．y1＞y2B．y1＜y2C．y1＝y2D．无法比较
【答案】B
【分析】判断出一次函数的增减性即可得到答案．
【解答】解：∵一次函数解析式为y＝2x+1，2＞0，
∴y随x增大而增大，
∵1＞﹣1，
∴y2＞y1，
故选：B．
【点评】本题主要考查了一次函数的增减性，正确记忆相关知识点是解题关键．
10．（3分）某单位准备与汽车租赁公司签订租车合同，以每月用车路程x千米计算，甲公司每月收取的租赁费为y1元，乙公司每月收取的租赁费为y2元，若y1、y2与x之间的函数关系如右图所示，其中x＝0对应的函数值为月固定租赁费，则下列判断中不一定正确的是（ ）
A．当月用车路程为2000千米时，两家公司租赁费相同
B．当月用车路程为2500千米时，租乙公司的车比较合算
C．除去月固定租赁费，甲公司每公里收取的费用比乙公司多
D．乙公司的月固定租赁费比甲公司多200元
【答案】D
【分析】观察函数图象可知，函数的横坐标表示路程，纵坐标表示收费，根据图象上特殊点的意义即可求出答案．
【解答】解：A、交点为（2000，2000），那么当月用车路程为2000km，两家汽车租赁公司租赁费用相同，说法正确，不符合题意；
B、由图象可得超过2000km时，相同路程，乙公司收费便宜，说法正确，不符合题意；
C、由图象易得乙的租赁费较高，当行驶2000千米时，总收费相同，那么可得甲租赁公司每公里收取的费用比乙租赁公司多，说法正确，不符合题意；
D、甲乙固定费用是函数与y轴交点，图中无法确定具体数值，故不能确定乙比甲多多少，说法错误，故本选项符合题意，
故选：D．
【点评】此题主要考查了一次函数的应用，解决本题的关键是理解两个函数图象交点的意义．
二、填空题（本大题6小题，每小题3分，共18分）请将下列各题的正确答案
11．（3分）﹣的相反数是 ．
【答案】见试题解答内容
【分析】根据只有符号不同的两个数互为相反数，可得答案．
【解答】解：﹣的相反数是，
故答案为：．
【点评】本题考查了实数的性质，在一个数的前面加上负号就是这个数的相反数．
12．（3分）16的算术平方根是 4 ．
【答案】见试题解答内容
【分析】运用算术平方根知识进行求解．
【解答】解：∵42＝16，
∴16的算术平方根是4，
故答案为：4．
【点评】此题考查了算术平方根的求解能力，关键是能准确理解并运用以上知识．
13．（3分）直线y＝﹣x+4与坐标轴围成的△ABO的面积是 8 ．
【答案】见试题解答内容
【分析】依据题意，首先求出直线y＝﹣x+4与x轴、y轴的交点的坐标，然后根据三角形的面积公式，得出结果．
【解答】解：∵y＝﹣x+4，
∴直线与x轴、y轴的交点的坐标分别为A（0，4），B（4，0），
∴S△AOB＝×4×4＝8．
故答案为：8．
【点评】本题主要考查的是一次函数图象上点的坐标特点，三角形的面积，解题时要能熟练掌握并理解“一次函数y＝kx+b与x轴的交点为（﹣，0），与y轴的交点为（0，b）”是关键．
14．（3分）如图，阴影部分是两个正方形，其它部分是两个直角三角形和一个正方形．若右边的直角三角形ABC中，AC＝17，BC＝15，则阴影部分的面积是 64 ．
【答案】见试题解答内容
【分析】根据勾股定理求出AB2，根据正方形的性质得到DF＝AB，根据勾股定理、正方形的面积公式计算即可．
【解答】解：由勾股定理得，AB2＝AC2﹣BC2＝172﹣152＝64，
∵四边形ABFD为正方形，
∴DF＝AB，
∴阴影部分的面积＝DE2+EF2＝DF2＝64，
故答案为：64．
【点评】本题考查的是勾股定理、正方形的性质，掌握如果直角三角形的两条直角边长分别是a，b，斜边长为c，那么a2+b2＝c2是解题的关键．
15．（3分）已知AB∥x轴，A的坐标为（2，6），AB＝4，则点B的坐标是 （6，6）或（﹣2，6） ．
【答案】（6，6）或（﹣2，6）．
【分析】根据平行于x轴的直线上点的坐标特征即可解决问题．
【解答】解：因为A的坐标为（2，6）且AB∥x轴，
所以点B的纵坐标为6．
又因为AB＝4，
则2+4＝6，4﹣4＝﹣2，
所以点B的坐标为（6，6）或（﹣2，6）．
故答案为：（6，6）或（﹣2，6）．
【点评】本题主要考查了坐标与图形性质，熟知平行于x轴的直线上点的坐标特征是解题的关键．
16．（3分）如图，教室的墙面ADEF与地面ABCD垂直，点P在墙面上．若PA＝AB＝5米，点P到AD的距离是3米，有一只蚂蚁要从点P爬到点B，它的最短行程是 4 米．
【答案】见试题解答内容
【分析】可将教室的墙面ADEF与地面ABCD展开，连接P、B，根据两点之间线段最短，利用勾股定理求解即可．
【解答】解：如图，将教室的墙面ADEF与地面ABCD展成一个平面，
过P作PG⊥BF于G，连接PB，
∵AG＝3米，AP＝AB＝5米，
∴PG＝4米，
∴BG＝8米，
∴PB＝＝4（米）．
故这只蚂蚁的最短行程应该是4米．
故答案为：4．
【点评】本题考查了平面展开﹣最短路径问题，立体图形中的最短距离，通常要转换为平面图形的两点间的线段长来进行解决．
三、速算题（每空1分，共10分）
17．（10分）①＝ 3 ；②＝ ±2 ；③＝ 0.6 ；④＝ 4 ；⑤＝ ；⑥＝ 2 ；⑦＝ 4 ；⑧＝ ；⑨＝ ；⑩＝ ．
【答案】①3；②±2；③0.6；④4；⑤；⑥2；⑦4；⑧；⑨；⑩．
【分析】分别根据二次根式的化简法则，平方根和立方根的定义，二次根式的运算法则计算即可．
【解答】解：①＝ 3；②±＝±2；③＝0.6；④＝4；⑤＝ ；⑥×＝2；⑦+＝4；⑧＝；⑨＝；⑩＝．
故答案为：①3；②±2；③0.6；④4；⑤；⑥2；⑦4；⑧；⑨；⑩．
【点评】本题考查了二次根式的性质与化简，平方根，立方根，二次根式的运算法则，熟练掌握这些运算法则是关键．
四、解答题（18题8分，19题6分，20-22题各8分，23题、24题各12分，共62分）
18．（8分）计算：
（1）；
（2）．
【答案】（1）2；
（2）14﹣4．
【分析】（1）先根据二次根式的乘法法则运算，然后化简二次根式后进行有理数的减法运算；
（2）先根据二次根式的除法法则和完全平方公式计算，然后合并即可．
【解答】解：（1）原式＝﹣
＝4﹣2
＝2；
（2）原式＝++2﹣6+9
＝3+2+2﹣6+9
＝14﹣4．
【点评】本题考查了二次根式的混合运算：熟练掌握二次根式的性质、二次根式的乘法法则和乘法公式是解决问题的关键．
19．（6分）如图，在平面直角坐标系xOy中，点A的坐标为（﹣4，4），点B的坐标为（﹣2，0），点C的坐标为（﹣1，2）．
（1）请画出△ABC关于y轴的对称图形△A1B1C1；
（2）直接写出点C1的坐标为 （1，2） ；（直接写出答案）
（3）点P在y轴上，且满足△PCC1的面积为3，直接写出点P坐标为 （0，5）或（0，﹣1） ．（直接写出答案）
【答案】（1）见解答．
（2）（1，2）．
（3）（0，5）或（0，﹣1）．
【分析】（1）根据轴对称的性质作图即可．
（2）由图可得答案．
（3）设点P坐标为（0，m），根据题意可列方程为＝3，求出m的值，即可得出答案．
【解答】解：（1）如图，△A1B1C1即为所求．
（2）由图可得，点C1的坐标为（1，2）．
故答案为：（1，2）．
（3）设点P坐标为（0，m），
∵△PCC1的面积为3，
∴＝3，
解得m＝5或﹣1，
∴点P坐标为（0，5）或（0，﹣1）．
故答案为：（0，5）或（0，﹣1）．
【点评】本题考查作图﹣轴对称变换，熟练掌握轴对称的性质是解答本题的关键．
20．（8分）图1是某品牌婴儿车，图2为其简化结构示意图，现测得AB＝CD＝6dm，BC＝3dm，AD＝9dm，其中AB与BD之间由一个固定为90°的零件连接（即∠ABD＝90°），根据安全标准需满足BC⊥CD，通过计算说明该车是否符合安全标准．
【答案】该车符合安全标准，证明见解析．
【分析】由勾股定理求出BD2＝45，再证BC2+CD2＝BD2，然后由勾股定理的逆定理得△BCD是直角三角形，∠BCD＝90°，即可得出结论．
【解答】解：该车符合安全标准，证明如下：
在Rt△ABD中，BD2＝AD2﹣AB2＝92﹣62＝45，
在△BCD中，BC2+CD2＝32+62＝45，
∴BC2+CD2＝BD2，
∴△BCD是直角三角形，∠BCD＝90°，
∴BC⊥CD，
∴该车符合安全标准．
【点评】本题主要考查了勾股定理的应用以及勾股定理的逆定理，熟练掌握勾股定理以及逆定理是解题的关键．
21．（8分）小明制作了一张面积为256cm2的正方形贺卡想寄给朋友．现有一个长方形信封如图所示，长、宽之比为3：2，面积为420cm2．
（1）求长方形信封的长和宽；
（2）小明能将贺卡不折叠就放入此信封吗？请通过计算给出判断．
【答案】见试题解答内容
【分析】（1）设长方形信封的长为3x cm，宽为2x cm，由长方形的面积可求出x的值，从而求出长方形信封的长和宽；
（2）先计算出正方形贺卡的边长，然后与长方形信封的宽进行比较，得出结论．
【解答】解：（1）设长方形信封的长为3x cm，宽为2x cm，
由题意得3x•2x＝420，
∴，
∴，，
答：长方形信封的长为，宽为；
（2）面积为256cm2的正方形贺卡的边长是16cm，
∵70＞64，
∴，
∴，即信封的宽大于正方形贺卡的边长，
∴小明能将这张贺卡不折叠就放入此信封．
【点评】本题考查了算术平方根的应用，熟练掌握算术平方根的运算是解题的关键．
22．（8分）我国传统的计重工具﹣﹣秤的应用，方便了人们的生活．如图①，可以用秤砣到秤纽的水平距离，来得出秤钩上所挂物体的重量．称重时，若秤杆上秤砣到秤纽的水平距离为x（厘米）时，秤钩所挂物重为y（斤），则y是x的一次函数．表中为若干次称重时所记录的一些数据．
（1）在表x，y的数据中，发现有一对数据记录错误．在图②中，通过描点的方法，观察判断哪一对数据是错误的？
（2）①求出y与x之间的函数解析式；
②秤杆上秤砣到秤纽的水平距离为16厘米时，秤钩所挂物重是多少？
【答案】（1）画图象见解答；x＝7，y＝2.75这组数据错误．
（2）4.5斤．
【分析】（1）利用描点法画出图形即可判断．
（2）设函数关系式为y＝kx+b，利用待定系数法解决问题即可．
【解答】解：（1）观察图象可知：x＝7，y＝2.75这组数据错误．
（2）设y＝kx+b，把x＝1，y＝0.75，x＝2，y＝1代入可得：
，
解得，
∴y＝，
当x＝16时，y＝4.5，
答：秤杆上秤砣到秤纽的水平距离为16厘米时，秤钩所挂物重是4.5斤．
【点评】本题考查一次函数的应用，待定系数法等知识，会用描点法画出函数图象，利用数形结合的思想是解题的关键．
23．（12分）在“勾股定理”一章的学习中，我们体会到了勾股定理应用的广泛性，以及“数形结合”是解决数学问题的一种重要的思想方法．
（1）【已有认识】既可以从算术平方根的角度理解，结合勾股定理的知识，也能将其看成是直角边都为1的直角三角形的斜边长，即，由此得到在数轴上寻找所表示的点的方法，如图1．
【拓展运用】如图2，点O、点A在数轴上，且OA＝2，AB＝1，AB⊥OA于A，以点O为圆心，OB长为半径画弧，交数轴于点P，则数轴中点P表示的数是 ．（直接写出答案）
（2）【已有认识】结合正方形网格，我们还可以表示某些长度为无理数的线段．
【拓展运用】请在图3正方形网格（每个小正方形的边长为1）内画出顶点在格点的△ABC，其中，，，并求出△ABC的面积，以及点C到AB边的距离．
（3）【已有认识】如图4，结合直角坐标系，我们发现：要求出坐标系中A、B两点的距离，显然是转化为求Rt△ABC的斜边长．下面以求DE为例来说明如何解决：
从坐标系中发现：D（﹣1，﹣4），E（6，﹣2），
所以DF＝|6﹣（﹣1）|＝7，EF＝|﹣2﹣（﹣4）|＝2，
所以由勾股定理可得，．
【拓展运用】①在图5中，设A（x1，y1），B（x2，y2），AC∥y轴，BC∥x轴，AC⊥BC于点C，则AC＝ y1﹣y2 ，BC＝ x1﹣x2 ，由此得到平面直角坐标系内任意两点间的距离公式，AB＝（直接写出答案）
②图4中，平面直角坐标系中有两点M（﹣3，4），N（﹣6，1），P为x轴上任一点，则PM+PN的最小值为 ；（直接写出答案）
③应用平面内两点间的距离公式，求代数式的最小值为： 3 .（直接写出答案）
【答案】（1）；
（2）2，；
（3）①y1﹣y2，x1﹣x2；
②；
③3．
【分析】（1）根据勾股定理，结合数轴即可得出结论；
（2）根据勾股定理的逆定理和三角形的面积公式即可得到结论；
（3）①根据题意列出代数式即可；
②利用轴对称求最短路线方法得出P点位置，进而求出PM+PN的最小值．
③把看成点（x，y）到两点（﹣1，2）和（5，﹣1）的距离之和，根据两点间的距离公式即可得到结论．
【解答】解：（1）∵OB＝＝＝，
∴OP＝OB＝，
∴数轴中点P表示的数是，
故答案为：；
（2）如图所示；
∵AC2+BC2＝2+8＝10＝AB2，
∴∠ACB＝90°，
∴△ABC的面积＝AC•BC＝××2＝2，
∴点C到AB边的距离＝2×2÷＝；
（3）①∵A（x1，y1），B（x2，y2），AC∥y轴，BC∥x轴，AC⊥BC，
∴AC＝y1﹣y2，BC＝x1﹣x2，
故答案为：y1﹣y2，x1﹣x2；
②如图，作点N关于x轴对称的点G，连接MG，直线MG与x轴的交点即为所求的点P．
∵N（﹣6，1），
∴G（﹣6，﹣1），
∵M（﹣3，4），
∴PM+PN＝PM+PG＝AMG＝＝，
即PM+PN的最小值为，
故答案为：；
③∵把式看成点（x，y）到两点（﹣1，2）和（5，﹣1）的距离之和，
∴两点（﹣1，2）和（5，﹣1）的距离是的最小值，
∴最小值为：＝3，
故答案为：3．
【点评】本题是三角形的综合题，考查了两点间的距离公式，勾股定理，轴对称﹣最短路径问题，勾股定理的逆定理，熟练掌握勾股定理和两点间的距离公式是解题的关键．
24．（12分）【阅读材料】建系法：通过构建平面直角坐标，借助点坐标、函数等方法，可以把几何关系转化成代数关系．【初步运用】某年广东省数学中考卷的填空压轴题：如图1，边长分别为6，4，2的三个正方形拼接在一起，它们的底边在同一直线上，则图中阴影部分（直角梯形）的面积为多少？
解决这道题目方法很多，其中一种就是“建系法”，请补全以下解题思路．（直接写出答案）
解题思路：
①如图2，以直线BC为x轴，以直线AB为y轴，以点B为原点建立直角坐标系．
②由题意得，点A坐标为（0，6），点G坐标为（6，4），点F坐标为 （10，4） ，点H坐标为（12，0）．
③由点A和点H的坐标求出直线AH的关系式为 y＝﹣x+6 ．
④因为点M的横坐标为6，且点M在直线AH上，所以代入横坐标即可求出纵坐标．
⑤同理求出点N坐标，从而得到线段GM和线段FN的长，从而求出阴影部分直角梯形的面积为 8 ．
【迁移探究】如图，长方形ABCD中，∠ABC＝∠BCD＝∠CDA＝∠DAB＝90°，AB＝CD＝4，AD＝BC＝6，AD∥BC，AB∥CD，点E是边AD上的一点，AE＝AB，BE交AC于点F．
（1）请用“建系法”求四边形EFCD的面积．（要求：建立直角坐标系时，把长方形的边放在坐标轴上，并把长方形置于第一象限．）
（2）在题（1）建立的直角坐标系基础下，点P是长方形AB边、AD边和CD边上的一个动点，沿着由B→A→D→C的方向移动，点Q是点P在运动过程中关于x轴的对称点．请问在点P的运动过程中，是否存在某一时刻使得△QBF是一个等腰三角形，若存在，请直接写出此时点Q的坐标；若不存在，请说明理由．
（3）在题（1）建立的直角坐标系基础下，把△ACD沿着直线AC折叠，点D的对应点为点D'，请直接写出点D′的坐标．
【答案】【阅读材料】（10，4），y＝﹣x+6，8．
【迁移探究】（1）S四边形EFCD＝．
（2）点Q的坐标为（0，﹣）或（6，﹣）．
（3）点D′的坐标为（，﹣）．
【分析】【阅读材料】以直线BC为x轴，以直线AB为y轴，以点B为原点建立直角坐标系．则A（0，6），G（6，4），F（10，4），H（12，0），运用待定系数法可求得直线AH的解析式，进而求得M（6，3），N（10，1），再利用梯形面积公式即可求得答案；
【迁移探究】（1）以直线BC为x轴，以直线AB为y轴，以点B为原点建立直角坐标系．则A（0，4），C（6，0），D（6，4），E（4，4），利用待定系数法可得：直线AC的解析式为y＝﹣x+4，直线BE的解析式为y＝x，联立方程组可求得点F的坐标，再由S四边形EFCD＝S△ACD﹣S△AEF，即可求得答案；
（2）分三种情况：当点P在AB边上时，当点P在AD边上时，当点P在CD边上时，分别求出点Q的坐标即可；
（3）由折叠得△ACD′≌△ACD，再证得△ACD≌△CAB（SAS），得出△ACD′≌△CAB，即点O、D′到AC的距离相等，推出OD′∥AC，可得直线OD′的解析式，设D′（t，﹣t），根据AD′＝AD＝6，建立方程求解即可得出答案．
【解答】解：【阅读材料】如图，以直线BC为x轴，以直线AB为y轴，以点B为原点建立直角坐标系．
则A（0，6），G（6，4），F（10，4），H（12，0），
设直线AH的解析式为y＝kx+b，把A（0，6），H（12，0）代入得，
解得：，
∴直线AH的解析式为y＝﹣x+6，
当x＝6时，y＝﹣×6+6＝3，
当x＝10时，y＝﹣×10+6＝1，
∴M（6，3），N（10，1），
∴GM＝4﹣3＝1，FN＝4﹣1＝3，
∴S四边形FGMN＝×（GM+FN）×FG＝×（1+3）×4＝8，
故答案为：（10，4），y＝﹣x+6，8．
【迁移探究】
（1）如图，以直线BC为x轴，以直线AB为y轴，以点B为原点建立直角坐标系．
∵AB＝CD＝4，AD＝BC＝6，AE＝AB，
∴A（0，4），C（6，0），D（6，4），E（4，4），
则直线AC的解析式为y＝﹣x+4，直线BE的解析式为y＝x，
联立得：，
解得：，
∴F（，），
∴S四边形EFCD＝S△ACD﹣S△AEF＝×6×4﹣×4×（4﹣）＝．
（2）存在．
∵F（，），B（0，0），
∴BF＝＝，
当点P在AB边上时，如图，
∵△QBF是一个等腰三角形，∠FBQ＝135°，
∴BQ＝BF，
∵点Q、P关于x轴对称，
∴BP＝BF，
∴OP＝OQ＝，
∴Q（0，﹣）；
当点P在AD边上时，BQ≥AB＝4，FQ≥4+＝，
且BQ＜FQ，
此时△BFQ不可能为等腰三角形；
当点P在CD边上时，如图，作OF的垂直平分线交DC的延长线于点Q，
设y＝﹣x+b，把OF的中点坐标（，）代入得：＝﹣+b，
解得：b＝，
∴OF的垂直平分线的解析式为y＝﹣x+，
当x＝6时，y＝﹣6+＝﹣，
∴Q（6，﹣）；
综上所述，点Q的坐标为（0，﹣）或（6，﹣）．
（3）由折叠得△ACD′≌△ACD，
在△ACD和△CAB中，
，
∴△ACD≌△CAB（SAS），
∴△ACD′≌△CAB，
∴点O、D′到AC的距离相等，
∴OD′∥AC，
∴直线OD′的解析式为y＝﹣x，
设D′（t，﹣t），如图，
则AD′＝AD＝6，
∴t2+（4+t）2＝36，
解得：t1＝﹣6（舍去），t2＝，
∴点D′的坐标为（，﹣）．
【点评】本题是一次函数综合题，考查了待定系数法，折叠的性质，等腰三角形的性质，全等三角形的判定和性质，建立平面直角坐标系将几何问题转化为代数问题是解题关键．
声明：试题解析著作权属所有，未经书面同意，不得复制发布日期：2024/11/25 0:36:34；用户：15008208124；邮箱：15008208124；学号：60148633x（厘米）
1
2
4
7
11
12
y（斤）
0.75
1.00
1.50
2.75
3.25
3.50
x（厘米）
1
2
4
7
11
12
y（斤）
0.75
1.00
1.50
2.75
3.25
3.50