四川省南充市阆中市东风中学2024-2025学年上学期九年级数学期中试卷

这是一份四川省南充市阆中市东风中学2024-2025学年上学期九年级数学期中试卷，共22页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．（4分）关于x的一元二次方程mx2+5x+m2﹣2m＝0的常数项为0，则m的值为（ ）
A．1B．2C．0或2D．0
2．（4分）函数y＝x2+3的图象经过点（﹣2，m），则m的值为（ ）
A．1B．7C．5D．4
3．（4分）已知关于x的一元二次方程x2+mx+3＝0的一个根是1，则方程的另一个根是（ ）
A．﹣3B．2C．3D．﹣4
4．（4分）如图，将三角形ABC绕点A逆时针旋转85°得到三角形AB′C′，若∠CAB′＝25°，则∠CAB＝（ ）
A．60°B．85°C．25°D．55°
5．（4分）用配方法解方程x2﹣4x﹣1＝0，将其化为（x+m）2＝k的形式，正确的是（ ）
A．（x+2）2＝3B．（x+2）2＝5C．（x﹣2）2＝3D．（x﹣2）2＝5
6．（4分）已知抛物线y＝ax2﹣2ax﹣a+1的顶点在x轴上，则a的值是（ ）
A．﹣2B．C．﹣1D．1
7．（4分）若关于x的一元二次方程x2+2x﹣m＝0有两个不相等的实数根，则m的取值范围是（ ）
A．m≥1B．m≤1C．m＞﹣1D．m＜﹣1
8．（4分）一次函数y＝ax+c（a≠0）与二次函数y＝ax2+bx+c（a≠0）在同一平面直角坐标系的图象可能是（ ）
A．B．
C．D．
9．（4分）某商品经过两次连续降价，每件售价由原来的100元降到了81元．设平均每次降价的百分率为x，则下列方程中正确的是（ ）
A．100（1+x）2＝81B．81（1+x）2＝100
C．100（1﹣x）2＝81D．81（1﹣x）2＝100
10．（4分）二次函数y＝ax2+bx+c（a≠0）的图象如图所示，下列结论：
①abc＜0；
②2a+b＝0；
③m为任意实数时，a+b≤m（am+b）；
④a﹣b+c＞0；
⑤若+bx1＝+bx2，且x1≠x2，则x1+x2＝2．其中正确的有（ ）
A．1个B．2个C．3个D．4个
二、填空题（本大题共6个小题，每小题4分，共24分）
11．（4分）若m是方程x2﹣5x﹣7＝0的根，则m2﹣5m+1的值等于 ．
12．（4分）将抛物线y＝x2﹣3先向上平移1个单位，再向右平移2个单位，所得抛物线的解析式为 ．
13．（4分）如图，抛物线y＝ax2与直线y＝bx+c的两个交点坐标分别为A（﹣3，6），B（1，3），则不等式ax2﹣bx﹣c≥0的解集是 ．
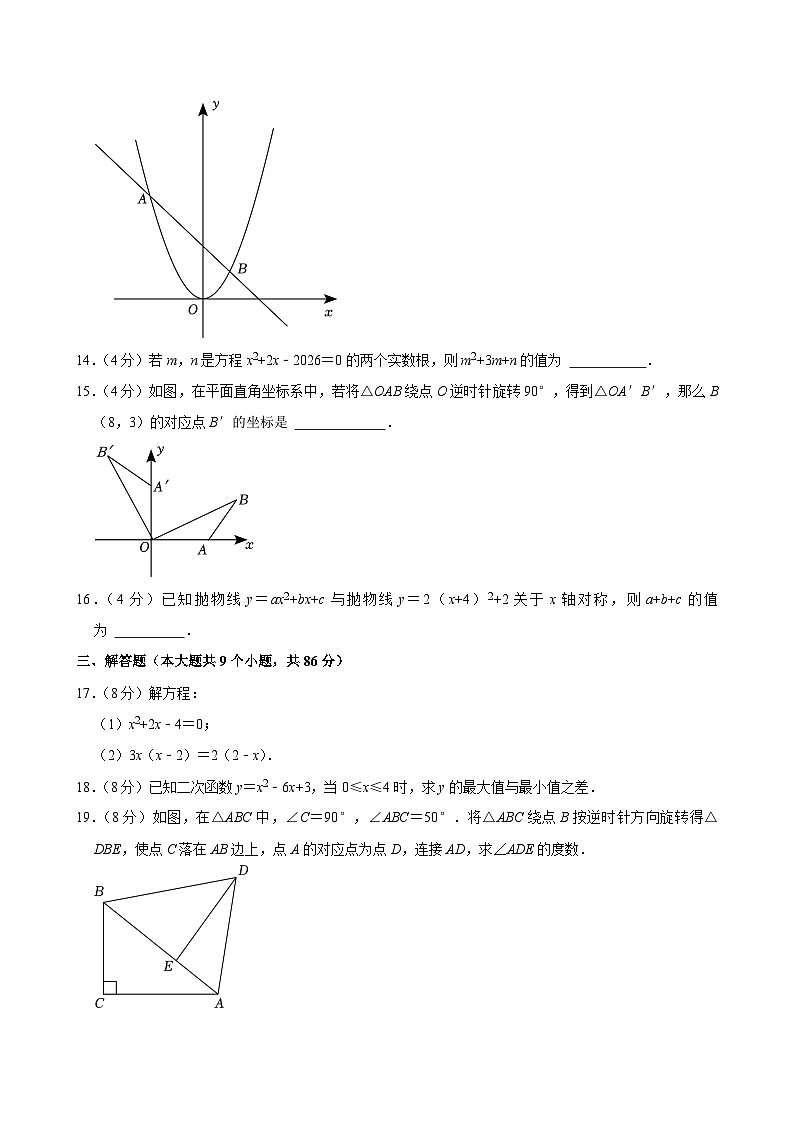
14．（4分）若m，n是方程x2+2x﹣2026＝0的两个实数根，则m2+3m+n的值为 ．
15．（4分）如图，在平面直角坐标系中，若将△OAB绕点O逆时针旋转90°，得到△OA′B′，那么B（8，3）的对应点B′的坐标是 ．
16．（4分）已知抛物线y＝ax2+bx+c与抛物线y＝2（x+4）2+2关于x轴对称，则a+b+c的值为 ．
三、解答题（本大题共9个小题，共86分）
17．（8分）解方程：
（1）x2+2x﹣4＝0；
（2）3x（x﹣2）＝2（2﹣x）．
18．（8分）已知二次函数y＝x2﹣6x+3，当0≤x≤4时，求y的最大值与最小值之差．
19．（8分）如图，在△ABC中，∠C＝90°，∠ABC＝50°．将△ABC绕点B按逆时针方向旋转得△DBE，使点C落在AB边上，点A的对应点为点D，连接AD，求∠ADE的度数．
20．（10分）如图，已知△ABC的三个顶点坐标分别是A（3，5），B（1，2），C（4，1）．
（1）根据要求画图：将△ABC绕原点O逆时针旋转90°后得到△A1B1C1；
（2）求△ABC的面积．
21．（10分）已知关于x的一元二次方程x2﹣2（k﹣1）x+k2+3＝0．
（1）若该方程有两个实数根，求k的取值范围；
（2）若该方程的两个实数根x1，x2满足（x1﹣1）（x2﹣1）＝14，求k的值．
22．（10分）图1是一座拱桥，拱桥的拱形呈抛物线形状，在拱桥中，当水面宽度为OA＝12米时，水面离桥洞最大距离为4米，如图2，以水平面为x轴，点O为原点建立平面直角坐标系．
（1）求该拱桥抛物线的解析式；
（2）当河水上涨，水面离桥洞的最大距离为2米时，求拱桥内水面的宽度．
23．（10分）某商场有A、B两种商品，一件B商品的售价比一件A商品的售价多5元，若用1500元购进A种商品的数量恰好是用900元购进B种商品的数量的2倍．
（1）求A、B两种商品每件售价各多少元；
（2）B商品每件的进价为20元，按原售价销售，该商场每天可销售B种商品100件，假设销售单价每上涨一元，B种商品每天的销售量就减少5件，设一件B商品售价a元，B种商品每天的销售利润为W元，求B种商品销售单价a为多少元时，B种商品每天的销售利润W最大，最大利润是多少元？
24．（10分）如图，点P是正方形ABCD内一点；AP＝1，BP＝，DP＝，△ADP绕点A顺时针旋转得到△ABP′，连接PP′，延长AP与BC相交于点Q．
（1）求线段PP′的长；
（2）求∠BPQ的大小；
（3）求正方形ABCD的边长．
25．（12分）如图所示，已知抛物线y＝ax2+bx﹣8（a≠0）经过点A（﹣2，0）、B（4，0），与直线y＝x﹣4交于B，D两点．
（1）求抛物线的解析式并直接写出D点的坐标；
（2）点P为直线BD下方抛物线上的一个动点，试求出△BDP面积的最大值及此时点P的坐标；
（3）在抛物线上有一点M，过点M作x轴的垂线交x轴于点N，若△AMN是等腰直角三角形，求点M的坐标．
2024-2025学年四川省南充市阆中市东风中学九年级（上）期中数学试卷
参考答案与试题解析
一、选择题（本大题共10个小题，每小题4分，共40分）
1．（4分）关于x的一元二次方程mx2+5x+m2﹣2m＝0的常数项为0，则m的值为（ ）
A．1B．2C．0或2D．0
【分析】根据二次项系数非零及方程的常数项为0，可得出关于m的一元一次不等式及一元二次方程，解之即可求出m的值．
【解答】解：∵关于x的一元二次方程mx2+5x+m2﹣2m＝0的常数项为0，
∴，
解得：m＝2，
∴m的值为2．
故选：B．
【点评】本题考查了一元二次方程的定义以及一元二次方程的一般形式，牢记“一元二次方程的二次项的系数不等于0”是解题的关键．
2．（4分）函数y＝x2+3的图象经过点（﹣2，m），则m的值为（ ）
A．1B．7C．5D．4
【分析】将点（﹣2，m）代入y＝x2+3计算即可求出m的值．
【解答】解：∵函数y＝x2+3的图象经过点（﹣2，m），
∴m＝（﹣2）2+3＝7，
故选：B．
【点评】本题考查了查二次函数图象上点的坐标特征，熟练掌握该知识点是关键．
3．（4分）已知关于x的一元二次方程x2+mx+3＝0的一个根是1，则方程的另一个根是（ ）
A．﹣3B．2C．3D．﹣4
【分析】设方程的一个根x1＝1，另一个根为x2，再根据根与系数的关系进行解答即可．
【解答】解：设方程的一个根x1＝1，另一个根为x2，根据题意得：
x1×x2＝3，
将x1＝1代入，得x2＝3．
故选：C．
【点评】本题考查了根与系数的关系，熟练掌握根与系数的关系的相关知识是解题的关键．
4．（4分）如图，将三角形ABC绕点A逆时针旋转85°得到三角形AB′C′，若∠CAB′＝25°，则∠CAB＝（ ）
A．60°B．85°C．25°D．55°
【分析】由旋转的性质得到∠C′AC＝85°，∠CAB＝∠C′AB′，根据角的和差关系进行计算，则可求出答案．
【解答】解：由旋转的性质得∠C′AC＝85°，∠CAB＝∠C′AB′，
∵∠CAB′＝25°，
∴∠CAB＝∠C′AB′＝∠C′AC﹣∠C′AB′＝85°﹣25°＝60°．
故选：A．
【点评】本题考查了旋转的性质，熟练掌握旋转的性质是本题的关键．
5．（4分）用配方法解方程x2﹣4x﹣1＝0，将其化为（x+m）2＝k的形式，正确的是（ ）
A．（x+2）2＝3B．（x+2）2＝5C．（x﹣2）2＝3D．（x﹣2）2＝5
【分析】移项，配方，即可得出选项．
【解答】解：x2﹣4x﹣1＝0，
x2﹣4x＝1，
x2﹣4x+4＝1+4，
（x﹣2）2＝5，
故选：D．
【点评】本题考查了解一元二次方程﹣配方法，能正确配方是解此题的关键．
6．（4分）已知抛物线y＝ax2﹣2ax﹣a+1的顶点在x轴上，则a的值是（ ）
A．﹣2B．C．﹣1D．1
【分析】把函数解析式整理出顶点式形式，然后根据顶点在x轴上，纵坐标等于0列方程求解即可．
【解答】解：y＝ax2﹣2ax﹣a+1＝a（x﹣1）2﹣2a+1，
∵抛物线顶点在x轴上，
∴﹣2a+1＝0，
解得a＝．
故选：B．
【点评】本题考查了二次函数的性质，把函数解析式整理成顶点式形式求解更简便．
7．（4分）若关于x的一元二次方程x2+2x﹣m＝0有两个不相等的实数根，则m的取值范围是（ ）
A．m≥1B．m≤1C．m＞﹣1D．m＜﹣1
【分析】根据判别式的意义得到Δ＝22+4m＞0，然后解不等式即可．
【解答】解：根据题意得Δ＝22+4m＞0，
解得m＞﹣1．
故选：C．
【点评】本题考查了一元二次方程ax2+bx+c＝0（a≠0）的根的判别式Δ＝b2﹣4ac：当Δ＞0，方程有两个不相等的实数根；当Δ＝0，方程有两个相等的实数根；当Δ＜0，方程没有实数根．
8．（4分）一次函数y＝ax+c（a≠0）与二次函数y＝ax2+bx+c（a≠0）在同一平面直角坐标系的图象可能是（ ）
A．B．
C．D．
【分析】根据直线和抛物线解析式知y＝ax+c与y＝ax2+bx+c与y轴交于同一点（0，c），据此可得．
【解答】解：在y＝ax+c中，当x＝0时，y＝c，
∴y＝ax+c与y轴的交点为（0，c）；
在y＝ax2+bx+c中，当x＝0时，y＝c，
∴y＝ax2+bx+c与y轴的交点为（0，c），
则y＝ax+c与y＝ax2+bx+c与y轴交于同一点（0，c），
故选：D．
【点评】本题考查二次函数的图象和一次函数的图象，解题的关键是明确一次函数和二次函数的性质．
9．（4分）某商品经过两次连续降价，每件售价由原来的100元降到了81元．设平均每次降价的百分率为x，则下列方程中正确的是（ ）
A．100（1+x）2＝81B．81（1+x）2＝100
C．100（1﹣x）2＝81D．81（1﹣x）2＝100
【分析】设平均每次降价的百分率为x，则等量关系为：原价×（1﹣x）2＝现价，据此列方程．
【解答】解：设平均每次降价的百分率为x，
由题意得，100（1﹣x）2＝81
故选：C．
【点评】本题考查了由实际问题抽象出一元二次方程，解答本题的关键是读懂题意，设出未知数，找出合适的等量关系，列方程．
10．（4分）二次函数y＝ax2+bx+c（a≠0）的图象如图所示，下列结论：
①abc＜0；
②2a+b＝0；
③m为任意实数时，a+b≤m（am+b）；
④a﹣b+c＞0；
⑤若+bx1＝+bx2，且x1≠x2，则x1+x2＝2．其中正确的有（ ）
A．1个B．2个C．3个D．4个
【分析】由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．
【解答】解：①抛物线开口方向向上，则a＞0．
抛物线对称轴位于y轴右侧，则a、b异号，即ab＜0．
抛物线与y轴交于y轴负半轴，则c＜0，
所以abc＜0．
故①错误；
②∵抛物线对称轴为直线x＝﹣＝1，
∴b＝﹣2a，即2a+b＝0，
故②正确；
③∵抛物线对称轴为直线x＝1，
∴函数的最小值为：a+b+c，
∴m为任意实数时，a+b≤m（am+b）；即a+b+c＜am2+bm+c，
故③正确；
④∵抛物线与x轴的一个交点在（3，0）的左侧，而对称轴为直线x＝1，
∴抛物线与x轴的另一个交点在（﹣1，0）的右侧，
∴当x＝﹣1时，y＞0，
∴a﹣b+c＞0，
故④正确；
⑤∵+bx1＝+bx2，
∴+bx1﹣﹣bx2＝0，
∴a（x1+x2）（x1﹣x2）+b（x1﹣x2）＝0，
∴（x1﹣x2）[a（x1+x2）+b]＝0，
而x1≠x2，
∴a（x1+x2）+b＝0，即x1+x2＝﹣，
∵b＝﹣2a，
∴x1+x2＝2，
故⑤正确．
综上所述，正确的有②③④⑤．
故选：D．
【点评】主要考查图象与二次函数系数之间的关系，会利用对称轴的范围求2a与b的关系，以及二次函数与方程之间的转换，根的判别式的熟练运用．
二、填空题（本大题共6个小题，每小题4分，共24分）
11．（4分）若m是方程x2﹣5x﹣7＝0的根，则m2﹣5m+1的值等于 8 ．
【分析】将x＝m代入原方程，可得出m2﹣5m＝7，再将其代入原式中，即可求出结论．
【解答】解：将x＝m代入原方程得：m2﹣5m﹣7＝0，
∴m2﹣5m＝7，
原式＝7+1＝8．
故答案为：8．
【点评】本题主要考查一元二次方程的根以及代数式求值，牢记“把方程的解代入原方程，等式左右两边相等”是解题的关键．
12．（4分）将抛物线y＝x2﹣3先向上平移1个单位，再向右平移2个单位，所得抛物线的解析式为 y＝（x﹣2）2﹣2 ．
【分析】根据抛物线的平移规律“上加下减，左加右减”求解即可．
【解答】解：将抛物线先向上平移1个单位，再向右平移2个单位后所得的抛物线是y＝（x﹣2）2﹣2．
故答案为：y＝（x﹣2）2﹣2．
【点评】本题考查二次函数图象的平移．掌握其平移规律“上加下减，左加右减”是解题关键．
13．（4分）如图，抛物线y＝ax2与直线y＝bx+c的两个交点坐标分别为A（﹣3，6），B（1，3），则不等式ax2﹣bx﹣c≥0的解集是 x≤﹣3 或 x≥1 ．
【分析】依据题意，由ax2﹣bx﹣c≥0得出ax2≥bx+c，即抛物线在直线上方的部分，根据图象和A，B的坐标即可确定答案．
【解答】解：由ax2﹣bx﹣c≥0得：ax2≥bx+c，
∴满足不等式的解为抛物线在直线上方的部分，
∴x≤﹣3或x≥1，
故答案为：x≤﹣3 或 x≥1．
【点评】本题主要考查了二次函数与不等式，正确运用数形结合是解题关键．
14．（4分）若m，n是方程x2+2x﹣2026＝0的两个实数根，则m2+3m+n的值为 2024 ．
【分析】根据m，n是方程x2+2x﹣2026＝0的两个实数根得到m2+2m＝2026，根据根与系数的关系得到m+n＝﹣2，据此利用整体代入法求解即可．
【解答】解：由题意得，m+n＝﹣＝﹣2，m2+2m﹣2026＝0，
∴m2+2m＝2026，
∴原式＝m2+2m+（m+n）
＝2026﹣2
＝2024．
故答案为：2024．
【点评】本题主要考查了一元二次方程的根与系数的关系，熟知x1，x2是一元二次方程ax2+bx+c＝0（a≠0）的两根时，x1+x2＝﹣，x1x2＝是解题的关键．
15．（4分）如图，在平面直角坐标系中，若将△OAB绕点O逆时针旋转90°，得到△OA′B′，那么B（8，3）的对应点B′的坐标是 （﹣3，8） ．
【分析】分别过点B和点B′作y轴的垂线，构造出全等三角形即可解决问题．
【解答】解：分别过点B和点B′作y轴的垂线，垂足分别为M和N，
由旋转可知，
∠B′OB＝90°，OB′＝OB，
∴∠B′ON+∠BOM＝∠BOM+∠OBM＝90°，
∴∠B′ON＝∠OBM．
在△B′ON和△OBM中，
，
∴△B′ON≌△OBM（AAS），
∴B′N＝OM，ON＝BM．
又∵点B坐标为（8，3），
∴B′N＝OM＝3，ON＝BM＝8，
∴点B′的坐标为（﹣3，8）．
故答案为：（﹣3，8）．
【点评】本题考查坐标与图形变化﹣旋转，熟知图形旋转的性质是解题的关键．
16．（4分）已知抛物线y＝ax2+bx+c与抛物线y＝2（x+4）2+2关于x轴对称，则a+b+c的值为 ﹣52 ．
【分析】利用关于x轴对称的点的坐标特点，纵坐标变为相反数，横坐标不变解答．
【解答】解：∵抛物线抛物线y＝ax2+bx+c与抛物线y＝2（x+4）2+2关于x轴对称，
∵y＝2（x+4）2+2＝2x2+16x+34，
函数y＝ax2+bx+c的解析式为：y＝﹣2x2+16×（﹣x）﹣34＝﹣2x2﹣16x﹣34，
∴a＝﹣2，b＝﹣16，c＝﹣34，
∴a+b+c＝﹣2﹣16﹣34＝﹣52，
故答案为：﹣52．
【点评】本题考查了二次函数图象与几何变换，掌握关于x轴对称的函数顶点横坐标相同，纵坐标互为相反数是解题的关键．
三、解答题（本大题共9个小题，共86分）
17．（8分）解方程：
（1）x2+2x﹣4＝0；
（2）3x（x﹣2）＝2（2﹣x）．
【分析】（1）利用配方法求解即可；
（2）利用因式分解法求解即可．
【解答】解：（1）∵x2+2x﹣4＝0，
∴x2+2x＝4，
则x2+2x+1＝4+1，即（x+1）2＝5，
∴x+1＝±，即x1＝﹣1+，x2＝﹣1﹣；
（2）∵3x（x﹣2）＝2（2﹣x），
∴3x（x﹣2）+2（x﹣2）＝0，
则（x﹣2）（3x+2）＝0，
∴x﹣2＝0或3x+2＝0，
解得x1＝2，x2＝﹣．
【点评】此题考查了解一元二次方程﹣因式分解法，熟练掌握因式分解的方法是解本题的关键．
18．（8分）已知二次函数y＝x2﹣6x+3，当0≤x≤4时，求y的最大值与最小值之差．
【分析】根据二次函数的增减性，求出0≤x≤4时，函数的最大值和最小值即可．
【解答】解：∵y＝x2﹣6x+3＝（x﹣3）2﹣6，
∴抛物线的开口向上，对称轴为直线x＝3，顶点坐标为（3，﹣6），
∴当x＝3时，y取得最小值，最小值为﹣6，
∵0≤x≤4，
∴当x＝0时，y取得最大值，此时y＝（0﹣3）2﹣6＝3．
∵3﹣（﹣6）＝9，
∴当0≤x≤4时，y的最大值与最小值之差为9．
【点评】本题考查求二次函数的最值，关键是求出在0≤x≤4时函数的最大值和最小值．
19．（8分）如图，在△ABC中，∠C＝90°，∠ABC＝50°．将△ABC绕点B按逆时针方向旋转得△DBE，使点C落在AB边上，点A的对应点为点D，连接AD，求∠ADE的度数．
【分析】由旋转得BA＝BD，通过等腰三角形及直角三角形可求∠ADE度数；
【解答】解：∵∠ABC＝90°，∠ABC＝50°，
∴∠CAB＝40°．
∵△ABC绕点B顺时针旋转得到△DBE，点E恰好在AB上，
∴BA＝BD，∠ABC＝∠DBA＝50°，
∴∠BAD＝∠ADB＝（180°﹣50°）＝65°，
∵∠BED＝∠ACB＝90°，
∴∠ADE＝∠ADB﹣∠DAB＝25°．
【点评】此题主要考查了旋转的性质，同时也利用了等腰三角形的性质，解题的关键是会确定旋转角．
20．（10分）如图，已知△ABC的三个顶点坐标分别是A（3，5），B（1，2），C（4，1）．
（1）根据要求画图：将△ABC绕原点O逆时针旋转90°后得到△A1B1C1；
（2）求△ABC的面积．
【分析】（1）根据旋转的性质作图即可；
（2）利用割补法求三角形的面积即可．
【解答】解：（1）如图，△A1B1C1即为所求．
（2）△ABC的面积是＝10﹣﹣3＝．
故答案为：．
【点评】本题考查作图﹣旋转变换，熟练掌握旋转的性质是解答本题的关键．
21．（10分）已知关于x的一元二次方程x2﹣2（k﹣1）x+k2+3＝0．
（1）若该方程有两个实数根，求k的取值范围；
（2）若该方程的两个实数根x1，x2满足（x1﹣1）（x2﹣1）＝14，求k的值．
【分析】（1）由该方程有两个实数根得到Δ≥0，然后解不等式即可；
（2）根据根与系数的关系得到，再根据（x1﹣1）（x2﹣1）＝14得到k2+3﹣（2k﹣2）+1＝14，然后解关于k的方程，最后利用k的范围确定k的值．
【解答】解：（1）根据题意得 Δ＝（2k﹣2）2﹣4（k2+3）≥0，
解得k≤﹣1；
（2）根据题意得：，
∵（x1﹣1）（x2﹣1）＝14，
∴x1x2﹣（x1+x2）+1＝14，
即 k2+3﹣（2k﹣2）+1＝14，
整理得 k2﹣2k﹣8＝0，
解得 k1＝﹣2，k2＝4，
∵k≤﹣1，
∴k＝﹣2．
【点评】本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c＝0（a≠0）的两根时，x1+x2＝﹣，x1x2＝．也考查了根的判别式．
22．（10分）图1是一座拱桥，拱桥的拱形呈抛物线形状，在拱桥中，当水面宽度为OA＝12米时，水面离桥洞最大距离为4米，如图2，以水平面为x轴，点O为原点建立平面直角坐标系．
（1）求该拱桥抛物线的解析式；
（2）当河水上涨，水面离桥洞的最大距离为2米时，求拱桥内水面的宽度．
【分析】（1）根据题意得出A（12，0），该抛物线顶点坐标为（6，4），设该抛物线解析式为y＝a（x﹣6）2+4，把A（12，0）代入求出a的值即可；
（2）根据题意得出水位上升了2米，把y＝2代入t＝﹣2x+80求出自变量的值，即可求解．
【解答】解：（1）∵OA＝12，
∴该抛物线的对称轴为直线，A（12，0），
∵水面离桥洞最大距离为4米，
∴该抛物线顶点坐标为（6，4），
设该抛物线解析式为y＝a（x﹣6）2+4，
把A（12，0）代入得：0＝a（12﹣6）2+4，
解得：，
∴该抛物线解析式为t＝﹣2x+80；
（2）4﹣2＝2（米），
∴水位上升了2米，
把y＝2代入t＝﹣2x+80得：，
解得：，．
（米），
答：拱桥内水面的宽度米．
【点评】本题主要考查了二次函数的应用，关键是根据题意找到等量关系式．
23．（10分）某商场有A、B两种商品，一件B商品的售价比一件A商品的售价多5元，若用1500元购进A种商品的数量恰好是用900元购进B种商品的数量的2倍．
（1）求A、B两种商品每件售价各多少元；
（2）B商品每件的进价为20元，按原售价销售，该商场每天可销售B种商品100件，假设销售单价每上涨一元，B种商品每天的销售量就减少5件，设一件B商品售价a元，B种商品每天的销售利润为W元，求B种商品销售单价a为多少元时，B种商品每天的销售利润W最大，最大利润是多少元？
【分析】（1）设A种商品每件售价x元，根据“用1500元购进A种商品的数量恰好是用900元购进B种商品的数量的2倍“列方程并检验，即可得到答案；
（2）W＝（a﹣20）[100﹣5×（a﹣30）]＝﹣5a2+350a﹣5000＝﹣5（a﹣35）2+1125，由二次函数性质可得答案．
【解答】解：（1）设A种商品每件售价x元，则B种商品每件售价（x+5）元，
∵用1500元购进A种商品的数量恰好是用900元购进B种商品的数量的2倍，
∴＝×2，
解得：x＝25，
经检验，x＝25是原方程的解，也符合题意，
∴x+5＝25+5＝30，
∴A种商品每件售价25元，B种商品每件售价30元；
（2）根据题意得：
W＝（a﹣20）[100﹣5×（a﹣30）]＝﹣5a2+350a﹣5000＝﹣5（a﹣35）2+1125，
∵﹣5＜0，
∴当a＝35时，W取最大值，最大值为1125元，
∴B种商品销售单价a为35元时，B种商品每天的销售利润W最大，最大利润是1125元．
【点评】本题考查二次函数的应用，涉及分式方程的应用，解题的关键是读懂题意，列出分式方程和函数关系式．
24．（10分）如图，点P是正方形ABCD内一点；AP＝1，BP＝，DP＝，△ADP绕点A顺时针旋转得到△ABP′，连接PP′，延长AP与BC相交于点Q．
（1）求线段PP′的长；
（2）求∠BPQ的大小；
（3）求正方形ABCD的边长．
【分析】（1）根据正方形的性质得AB＝AD，∠BAD＝90°，再利用旋转的性质得AP＝AP′，∠PAP′＝∠DAB＝90°，于是可判断△APP′是等腰直角三角形，根据等腰直角三角形的性质得PP′＝PA＝；
（2）由等腰直角三角形性质知∠APP′＝45°，利用旋转的性质得PD＝P′B＝，接着根据勾股定理的逆定理可证明△PP′B为直角三角形，∠P′PB＝90°，然后利用平角定义计算∠BPQ的度数；
（3）作BE⊥AQ，垂足为E，由∠BPQ＝45°，P′B＝2，求出PE＝BE＝2，在Rt△ABE中，运用勾股定理求出AB．
【解答】解：（1）∵四边形ABCD为正方形，
∴AB＝AD，∠BAD＝90°，
∵△ADP沿点A旋转至△ABP′，
∴AP＝AP′＝1，PD＝P′B＝，∠PAP′＝∠DAB＝90°，
∴△APP′是等腰直角三角形，
∴PP′＝＝；
（2）∵△APP′是等腰直角三角形，
∴∠APP′＝45°，
在△PP′B中，PP′＝，PB＝2，P′B＝，
∵（）2+（2）2＝（）2，
∴PP′2+PB2＝P′B2，
∴△PP′B为直角三角形，∠P′PB＝90°，
∴∠BPQ＝180°﹣∠APP′﹣∠P′PB＝180°﹣45°﹣90°＝45°；
（3）作BE⊥AQ，垂足为E，
∵∠BPQ＝45°，PB＝2，
∴PE＝BE＝2，
∴AE＝2+1＝3，
∴AB＝＝＝．
【点评】本题考查了旋转的性质，勾股定理，正方形的性质，解答本题的关键要明确：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．
25．（12分）如图所示，已知抛物线y＝ax2+bx﹣8（a≠0）经过点A（﹣2，0）、B（4，0），与直线y＝x﹣4交于B，D两点．
（1）求抛物线的解析式并直接写出D点的坐标；
（2）点P为直线BD下方抛物线上的一个动点，试求出△BDP面积的最大值及此时点P的坐标；
（3）在抛物线上有一点M，过点M作x轴的垂线交x轴于点N，若△AMN是等腰直角三角形，求点M的坐标．
【分析】（1）设抛物线的解析式为y＝a（x+2）（x﹣4），将点C的坐标代入可求得a的值，然后将y＝x﹣4与抛物线的解析式联立方程组并求解即可；
（2）过点P作PE∥y轴，交直线AB与点E，设P（x，x2﹣2x﹣8），则E（x，x﹣4），则PE＝﹣x2+3x+4，然后依据S△BDP＝S△DPE+S△BPE，列出△BDP的面积与x的函数关系式，然后依据二次函数的性质求解即可；
（3）设点N的坐标为（m，0）则点M（m，m2﹣2m﹣8），则AN＝|m+2|，MN＝|m2﹣2m﹣8|，进而得到|m+2|＝|m2﹣2m﹣8|，解答即可得到m的值，进而得到点M的坐标为（5，7）或（3，﹣5）．
【解答】解：（1）已知抛物线y＝ax2+bx﹣8（a≠0）经过点A（﹣2，0）、B（4，0），将点A，点B的坐标代入得：
，
解得：，
∴设该抛物线解析式为y＝x2﹣2x﹣8，
联立方程组：，
解得（舍去）或，
即点D的坐标是（﹣1，﹣5）；
（2）如图1：过点P作PE∥y轴，交BD于点E，
设P（x，x2﹣2x﹣8），则E（x，x﹣4）．
∴PE＝x﹣4﹣（x2﹣2x﹣8）＝﹣x2+3x+4．
∴S△BDP＝S△DPE+S△BPE＝PE•（xp﹣xD）+PE••（xB﹣xE）＝PE•（xB﹣xD）＝（﹣x2+3x+4）＝﹣（x﹣）2+．
∴当x＝时，△BDP的面积的最大值为．
∴P（，﹣）．
（3）如图2，
∵MN⊥x轴于N，
∴∠MNA＝90°，
∵△AMN是等腰直角三角形，
∴AN＝MN，
∵点P在抛物线y＝x2﹣2x﹣8上，
∴设点N的坐标为（m，0）则点M（m，m2﹣2m﹣8），
∴AN＝|m﹣（﹣2）|＝|m+2|，MN＝|m2﹣2m﹣8|，
∴|m+2|＝|m2﹣2m﹣8|，
∴m+2＝m2﹣2m﹣8或m+2＝﹣（m2﹣2m﹣8），
即m2﹣3m﹣10＝0或m2﹣m﹣6＝0，
当m2﹣3m﹣10＝0时，
解得m＝5或m＝﹣2（舍去），
此时M（5，7）；
当m2﹣m﹣6＝0时，
解得m＝3或m＝﹣2（舍去），
此时M（3，﹣5），
综上，点M的坐标为（5，7）或（3，﹣5）．
【点评】本题属于二次函数综合题，主要考查了二次函数的性质，待定系数法求二次函数的表达式，等腰直角三角形的判定等知识点，分类讨论是解答本题的关键．