2024年山东省济宁市汶上县中考二模数学模拟试题(无答案)

这是一份2024年山东省济宁市汶上县中考二模数学模拟试题(无答案)，共6页。试卷主要包含了已知反比例函数，有结论等内容，欢迎下载使用。

注意事项：
1.本试题分第Ⅰ卷和第Ⅱ卷两部分，第Ⅰ卷为选择题，30分；第Ⅱ卷为非选择题，70分；共100分，考试时间为120分钟.
2.答第Ⅰ卷前务必每题选出答案后，都必须用2B铅笔把答题卡上对应题目的答案标号（ABCD）涂黑，如需改动，必须先用橡皮擦干净，再改涂其他答案。
3.答第Ⅱ卷时，将密封线内的项目填写清楚，在题号所示答题区域作答，答题作图时，先用2B铅笔试画，无误后用黑色签字笔描黑.
4.填空题请直接将答案填写在答题卡上，解答题应写出文字说明、证明过程或演算步骤.
第Ⅰ卷（选择题 共30分）
一、选择题（本大题共10个小题，每小题3分，共30分.）
1.党的二十大报告指出，我国将建成世界上规模最大的教育体系、社会保障体系、医疗卫生体系，教育普及水平实现历史性跨越，基本养老保险覆盖十亿四千万人，基本医疗保险参保率稳定在百分之九十五以上，将数据1040000000用科学记数法表示为（ ）
A.B.C.D.
2.在一个不透明的塑料袋中装有红色球、白色球共40个，除颜色外其他都相同.小明通过多次摸球试验后发现，摸到红色球的频率稳定在20%左右，则塑料袋中红色球可能有（ ）
A.6个B.7个C.8个D.9个
3.用配方法解方程，配方正确的是（ ）
A.B.C.D.
4.在中，，，则的值是（ ）
A.B.C.1D.
5.如图，在中，点D，E分别是，的中点，连接.若，则（ ）
A.1B.2C.3D.4
6.如图，在中，，，，将绕点A顺时针旋转90°得到，连接，则的长为（ ）
A.4B.6C.D.
7.已知反比例函数，有结论：①图象必经过；②图象在二、四象限内；③y随x的增大而增大；④当时，则.其中错误的结论有（ ）
A.3个B.2个C.1个D.0个
8.如图，，是的两条切线，点A，B是切点，点C为上一点，若，则的度数为（ ）
A.70°B.50°C.20°D.40°
9.我县某超市经营一种商品，在销售过程中，发现一周利润y（元）与每件销售价x（元）之间的关系满足，由于某种原因，售价x（元）需满足，那么该超市这一周可获得最大利润为（ ）
A.1554元B.1556元C.1558元D.1560元
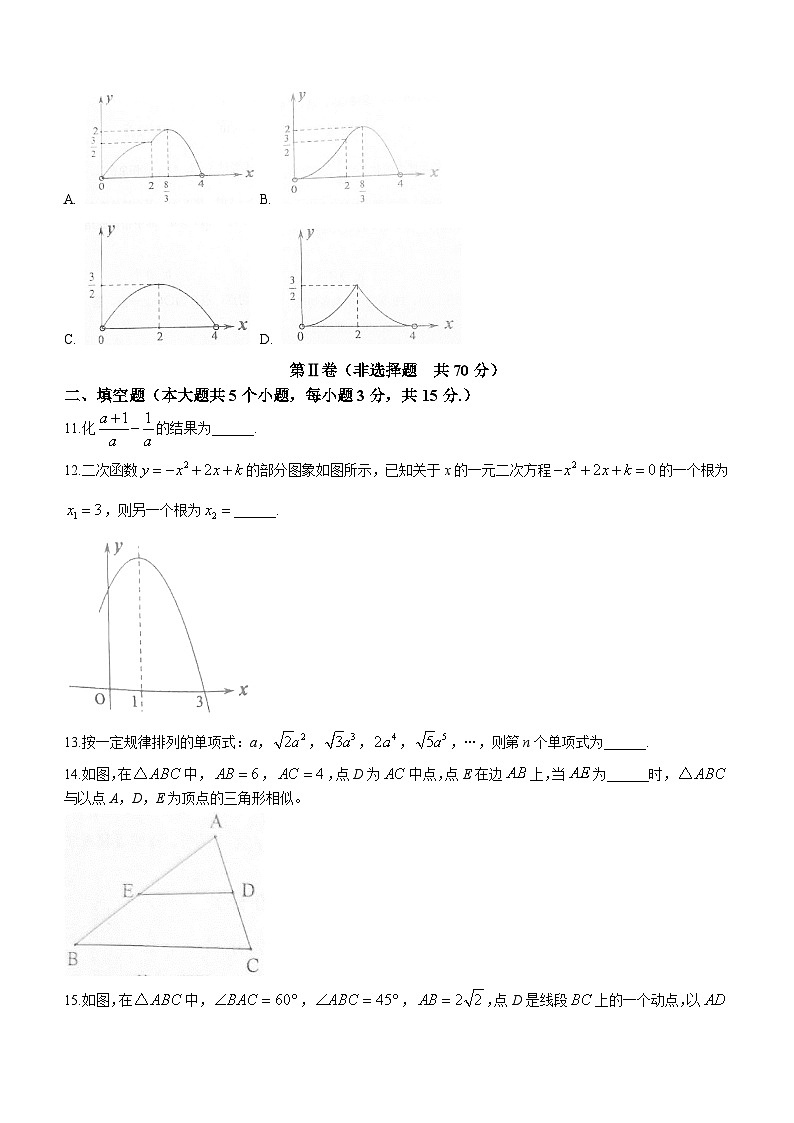
10.如图，在中，，，，点D是边上一动点（不与A、C两点重合），沿的路径移动，过点D作，交于点E，将沿直线折叠得到，若设，与重叠部分的面积为y，则下列图象能大致反映y与x之间的函数关系的是（ ）
A. B.
C. D.
第Ⅱ卷（非选择题 共70分）
二、填空题（本大题共5个小题，每小题3分，共15分.）
11.化的结果为______.
12.二次函数的部分图象如图所示，已知关于x的一元二次方程的一个根为，则另一个根为______.
13.按一定规律排列的单项式：a，，，，，…，则第n个单项式为______.
14.如图，在中，，，点D为中点，点E在边上，当为______时，与以点A，D，E为顶点的三角形相似。
15.如图，在中，，，，点D是线段上的一个动点，以为直径画分别交，于点E，F，连接，则线段长度的最小值为______.
三、解答题（本大题共7个小题，共55分，解答时应写出证明过程或演算步骤.）
16.（本题满分5分）
计算：.
17.（本题满分6分）
2023年5月30日上午，神舟十六号载人飞船成功发射，举国振奋.为使同学们进一步了解中国航天科技的快速发展，我县某中学九（1）班团支部组织了一场手抄报比赛，要求该班每位同学从A：“北斗”，B：“5G时代”，C：“东风快递”，D：“智轨快运”四个主题中任选一个自己喜爱的主题，比赛结束后，该班团支部统计了同学们所选主题的频数，绘制成如图两种不完整的统计图，请根据统计图中的信息解答下列问题.
（1）九（1）班共有______名学生；
（2）补全图1中的折线统计图；
（3）若贾林和王峰两位同学分别从A，B，C，D四个主题中任选一个主题，请用列表或画树状图的方法求出他们选择相同主题的概率.
图1 图2
18.（本题满分7分）
已知关于x的一元二次方程有两个不相等的实数根.
（1）求m的取值范围；
（2）当m取满足条件的最小奇数时，求方程的根.
19.（本题满分7分）
为了防洪需要，汶上溢流坝决定新建一座拦水坝.如图，拦水坝的横截面为四边形，其中，，斜面的坡度（指坡面的铅直高度与水平宽度的比），已知斜坡的长度为20米，，求斜坡的长度.（结果精确到0.1米，参考数据：，，）
20.（本题满分9分）
某同学借助反比例函数的图象设计了“鱼形”图案.如图，在平面直角坐标系中，以反比例函数图象上的点和点B为顶点，分别作菱形和菱形，点D，E在x轴上，以点O为圆心，长为半径作，连接.
（1）求k的值；
（2）求扇形的半径及圆心角的度数；
（3）求图中阴影部分面积之和.
21.（本题满分10分）
【初步感知】
（1）如图1，点A，B，P均在上，若，则锐角的大小为______度；
【深入探究】
（2）如图2，小明遇到这样一个问题：是等边三角形的外接圆，点P在上（点P不与点A，C重合），连接，，.求证：；小明发现，延长至点E，使，连接，通过证明.可推得是等边三角形，进而得证.请根据小明的分析思路完成证明过程.
【启发应用】
（3）如图3，是的外接圆，，，点P在上，且点P与点B在的两侧，连接，，，若，则的值为______.
图1 图2 图3
22.（本题满分11分）
如图1，在平面直角坐标系中，抛物线过点，和，作直线，点为抛物线上一动点，过点P作轴交直线于点M，交x轴于点N.
图1 图2 备用图
（1）直接写出抛物线和直线的解析式；
（2）如图2，连接，当为等腰三角形时，求m的值；
（3）当P点在运动的过程中，在y轴上是否存在点Q，使得以点O，P，Q为顶点的三角形与以点B，C，N为顶点的三角形相似（其中点P与点C相对应），若存在，直接写出点Q的坐标；若不存在，请说明理由.