2024年山东省淄博市博山区九年级中考一模数学模拟试题(无答案)

这是一份2024年山东省淄博市博山区九年级中考一模数学模拟试题(无答案)，共6页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1. 冬季奥林匹克运动会（简称冬奥会）是世界规模最大的冬季综合性运动会，每四年举办一届．第24届冬奥会将于2022年2月4日在北京开幕、下列四个图分别是四届冬奥会图标中的一部分，其中不是轴对称图形的为（ ）
A. B.
C. D.
2. 为抗击新冠肺炎，国家大力提高口罩产能，据统计，我国一月份口罩产量达到42亿只，42亿用科学记数法表示为（ ）
A B. C. D.
3. 下列语句正确的是（ ）．
A. 延长射线ABB. 线段MN叫做点M，N间的距离
C. 两点之间，直线最短D. 直线a，b相交于点P
5. 已知，则的值为（ ）
A. 6B. －6C. 3D. 9
6. 实数在数轴上对应点的位置如图所示，下列结论正确的是（ ）
A. B. C. D.
7. 每周四下午的活动课是学校的特色课程，同学们可以选择自己喜欢的课程．小明和小丽从“二胡课”“轮滑课”“围棋课”三种课程中随机选择一种参加，则两人恰好选择同一种课程的概率是（ ）
A. B. C. D.
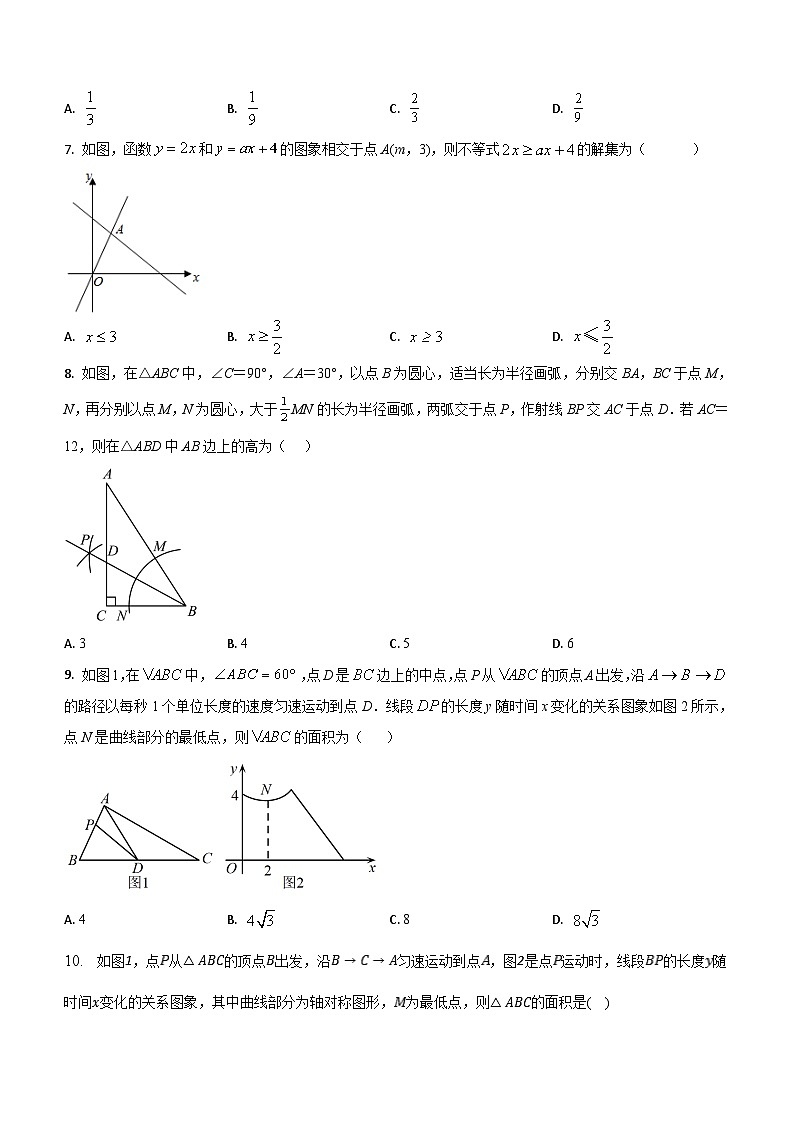
7. 如图，函数和的图象相交于点A(m，3)，则不等式的解集为（ ）
A. B. C. D.
8. 如图，在△ABC中，∠C＝90°，∠A＝30°，以点B为圆心，适当长为半径画弧，分别交BA，BC于点M，N，再分别以点M，N为圆心，大于MN的长为半径画弧，两弧交于点P，作射线BP交AC于点D．若AC＝12，则在△ABD中AB边上的高为（ ）
A. 3B. 4C. 5D. 6
9. 如图1，在中，，点D是边上的中点，点P从的顶点A出发，沿的路径以每秒1个单位长度的速度匀速运动到点D．线段的长度y随时间x变化的关系图象如图2所示，点N是曲线部分的最低点，则的面积为（ ）
A. 4B. C. 8D.
10. 如图，点从的顶点出发，沿匀速运动到点，图是点运动时，线段的长度随时间变化的关系图象，其中曲线部分为轴对称图形，为最低点，则的面积是( )
A. B. C. D.
二、填空题（本大题共6个小题，每小题4分，共24分．把答案填在题中的横线上.）
11.若关于x的一元二次方程(k-2)x2-2kx+k=6有实数根,则k的取值范围为 .
12.如图，四边形ABCD是矩形，AB=5，BC=8，点P在AB上，AP=1,把矩形ABCD沿CP折叠，点B落在点B`处，B`P,B`C分别与AD交于点E点F,则EF= ．
13.如图，一架无人机在空中A处观测到山顶B的仰角为，山顶B在水中的倒影C的俯角为，此时无人机距水面的距离米，则点B到水面距离的高度为 ．（参考数据：，，，，，）
14．已知关于x的一元二次方程x2+kx﹣6＝0的一个根是2，则另一个根是 ．
15．一列慢车从A地驶往B地，一列快车从B地驶往A地，两车同时出发，分别驶向目的地后停止．如图，折线表示两车之间的距离y（千米）与慢车行驶时间t（小时）之间的关系，求当快车到达A地时，慢车与B地的距离为 千米．
17. 18.
16．如图，在正方形ABCD中，点E是边CD上一点，BF⊥AE，垂足为F，将正方形沿AE，BF切割分成三块，再将△ABF和△ADE分别平移，拼成矩形BGHF．若BG＝nBF，则＝ （用含n的式子表示）．
三、解答题：（解答要写出必要的文字说明、证明过程或推演步骤.）
17.
（1）计算：；
（2）解不等式组，并把它们的解集表示在数轴上.
18.先化简，再求值：，且的值满足.
19. 初三（1）班针对“垃圾分类”知晓情况对全班学生进行专题调查活动，对“垃圾分类”的知晓情况分为A、B、C、D四类．其中，A类表示“非常了解”，B类表示“比较了解”，C类表示“基本了解”，D类表示“不太了解”，每名学生可根据自己的情况任选其中一类，班长根据调查结果进行了统计，并绘制成了不完整的条形统计图和扇形统计图．
根据以上信息解决下列问题：
（1）初三（1）班参加这次调查的学生有 人，扇形统计图中类别C所对应扇形的圆心角度数为 °；
（2）求出类别B的学生数，并补全条形统计图；
（3）类别A的4名学生中有2名男生和2名女生，现从这4名学生中随机选取2名学生参加学校“垃圾分类”知识竞赛，请用列举法（画树状图或列表）求所选取的2名学生中恰好有1名男生、1名女生的概率．
20. 如图，在Rt△ABC中，∠BAC=90°，点D为BC边的中点，以AD为直径作⊙O，分别与AB，AC交于点E，F，过点E作EG⊥BC于G．
（1）求证：EG是⊙O切线；
（2）若AF=6，⊙O的半径为5，求BE的长．
21. 我们给出如下定义：若一个四边形中存在相邻两边的平方和等于一条对角线的平方，则称这个四边形为勾股四边形，这两条相邻的边称为这个四边形的勾股边．
（1）写出你所学过的特殊四边形中是勾股四边形的两种图形的名称________，________．
（2）如图（1），已知格点（小正方形的顶点），，，请你直接写出一个以格点为顶点，，为勾股边且对角线相等的勾股四边形的顶点M的坐标为________；
（3）如图（2），将绕顶点B按顺时针方向旋转60°，得到，连接，，．求证：，即四边形是勾股四边形；
（4）若将图（2）中绕顶点B按顺时针方向旋转a度，得到，连接，，则________°，四边形是勾股四边形．
22. 某玩具商场内有形形色色的玩具，其中两种玩具最受孩子们欢迎．已知1个种玩具和2个种玩具共卖360元，2个种玩具和3个种玩具共卖640元．
（1）两种玩具的单价各是多少元？
（2）某机构计划团购两种玩具共15个，其中种玩具的数量不超过种玩具数量的，则该机构购买多少个种玩具花费最低？最低花费为多少元？
23. 小明在课余时间，找了几副度数不同的近视镜，让镜片正对着太阳光，并上下移动镜片，直到地上的光斑最小．此时他测量了镜片到光斑的距离，得到如下数据：
（x表示镜片到光斑的距离，y表示镜片的度数）
为了进一步研究镜片度数y与镜片到光斑的距离x间的关系，小明借助计算机绘制了表示变量间关系的图象，并给出了它们的关系式，如图：

（1）m的值是______；
（2）小亮的眼镜是近视200度，用小亮的眼镜做实验的话，请写出其镜片到光斑的距离，并解释你是怎样得出这一结论的；
（3）根据图表中信息，发现随着x的逐渐变大，y的变化趋势是________；
（4）你来预测一下，如果是一副平光镜（近视度数为0），会不会有光斑存在？（直接写结论，无需解释）
镜片度数y/度
…
400
625
800
m
…
镜片到光斑的距离x/m
…
0.25
0.16
0.125
0.10
…