2024-2025学年山东省日照市岚山区九年级(上)11月期中数学试卷(解析版)

这是一份2024-2025学年山东省日照市岚山区九年级(上)11月期中数学试卷(解析版)，共20页。试卷主要包含了第Ⅱ卷必须用0等内容，欢迎下载使用。
注意事项：
1．本试题分第Ⅰ卷和第Ⅱ卷两部分，共6页．满分120分．考试时间为120分钟．
2．答卷前务必将自己的姓名、考号等信息填写在答题卡规定位置上．考试结束，本试卷和答题卡一并收回．
3．第Ⅰ卷每小题选出答案后，必须用2B铅笔把答题卡上对应题号的答案标号涂黑．如需改动，必须先用橡皮擦干净，再改涂其他答案．不涂在答题卡上，答在试卷上无效．
4．第Ⅱ卷必须用0．5毫米黑色签字笔作答，答案须写在答题卡各题目指定的区域内，在试卷上答题不得分；如需改动，先划掉原来的答案，然后再写上新的答案．
第Ⅰ卷（选择题30分）
一、选择题（本大题共10小题，每小题3分，满分30分．在每小题所给出的四个选项中，只有一项是符合题目要求的，请将正确选项的字母代号填涂在答题卡相应位置上）
1. 下列各曲线是根据不同的函数绘制而成的，其中是中心对称图形的是（ ）
A. B.
C. D.
【答案】C
【解析】A.不是中心对称图形，不符合题意；
B.不是中心对称图形，不符合题意；
C.是中心对称图形，符合题意；
D.不是中心对称图形，不符合题意；
故选：C．
2. 若是方程的一个根，则此方程的另一个根是( )
A. -1B. 0C. 1D. 2
【答案】C
【解析】设另一个根为，依题意，，
∴，
故选：C．
3. 将抛物线向右平移3个单位后得到新抛物线的顶点坐标为（ ）
A. B. C. D.
【答案】B
【解析】因为，
所以抛物线的顶点坐标为，
所以将此抛物线向右平移3个单位长度后，所得新抛物线的顶点坐标为．
故选：B．
4. 下列说法中，正确的是（ ）
A. 成中心对称的两个三角形的对应边互相平行且相等
B. 平分弦的直径垂直于弦
C. 等弦所对的圆周角相等
D. 旋转前后两个图形对应点连线的中垂线都经过旋转中心
【答案】D
【解析】A、成中心对称的两个三角形的对应边一定相等且平行或在同一条直线上，所以A选项错误，不符合题意；
B、平分弦（非直径）的直径垂直于弦，并且平分弦所对的弧，所以B选项错误，不符合题意；
C、在同圆和等圆中，等弦所对的圆周角相等，所以C选项错误，不符合题意；
D、旋转前后两个图形对应点连线的中垂线都经过旋转中心，所以D选项正确，符合题意；
故选：D．
5. 如图，是半圆O的直径，C为半圆O上一点，以点B为圆心，适当长为半径画弧，交于点M，交于点N，分别以点M，N为圆心，大于的长为半径画弧，两弧在的内部相交于点D，画射线，连接．若，则的度数是（ ）
A. B. C. D.
【答案】B
【解析】是半圆的直径，
，
，
，
由题意得，为的平分线，
．
故选：B．
6. 为更好地落实劳动课程，学校将实践基地“分田到班”，九（1）班分到如图所示一块长为，宽为的矩形空地，计划分割出两块完全相同的矩形菜地（阴影部分）用来种植蔬菜，菜地四周空白部分为宽度相等的人行道，若菜地的面积之和为．设人行道的宽度为，则列出关于x的方程应为（ ）
A. B.
C. D.
【答案】B
【解析】若人行道的宽度都为，由题意，得：；故选：B．
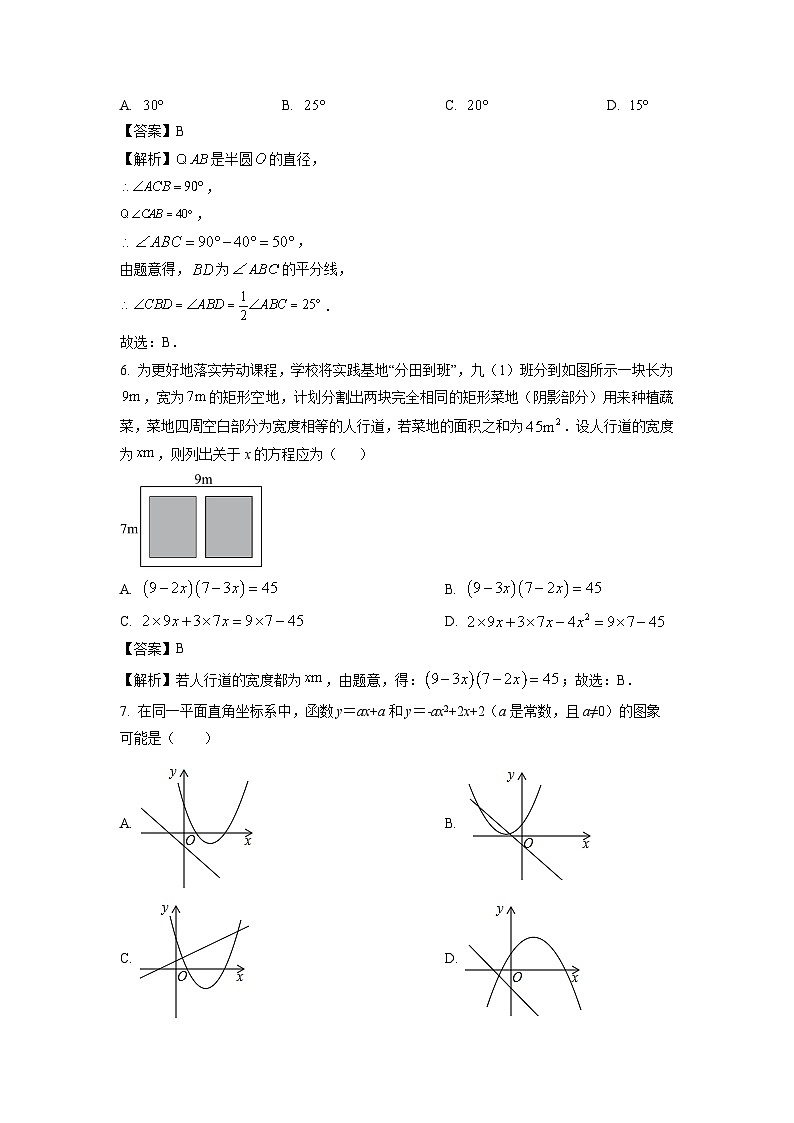
7. 在同一平面直角坐标系中，函数y＝ax+a和y＝-ax2+2x+2（a是常数，且a≠0）的图象可能是（ ）
A. B.
C. D.
【答案】B
【解析】当时，函数的图象经过一、二、三象限；函数的开口向下，对称轴在y轴的右侧；
当时，函数的图象经过二、三、四象限；函数的开口向上，对称轴在y轴的左侧，故B正确．
故选B．
8. 如图，在中，，其内切圆分别与、、相切于点D、E、F，若，，则圆的半径为（ ）
A. 2B. 4C. 5D. 3
【答案】D
【解析】如图，设在内切圆圆心为点，连接，
内切圆分别与、、相切于点、、，
，，，，
，
四边形是矩形，
，
四边形是正方形，
，
在中，，
，
解得：（负值舍去），
，
圆的半径为3，
故选：D．
9. 雪花也称银粟，是天空中的水汽经凝华而来的固态降水，多呈六角形，是一种美丽的结晶．美术课要求绘制雪花，小华利用数学知识作出如下操作：建立如图所示的平面直角坐标系，绘制菱形，且顶点B的坐标为0,4，点A在第一象限，，将菱形绕原点O沿顺时针方向旋转，每次旋转，旋转第一次得到四边形（点与点A重合），则旋转第2024次得到的点的坐标是（ ）
A. B.
C. D.
【答案】C
【解析】∵，
∴旋转周期为6个，
，
∴旋转第2024次得到的菱形与第二次得到的菱形相同，
如图，旋转第二次得到菱形，
过作轴于，连接交于，
四边形是菱形，
，，，
的坐标是0,4，
，
，
，
，
，
，
，
，
的坐标是．
点的坐标是．
故选：C．
10. 如图，抛物线，与x轴正半轴交于A，B两点，交y轴负半轴于点C．下列结论：①；②；③若点B的坐标为，且，则；④若抛物线的对称轴是直线，m为任意实数，则．其中正确的个数有（ ）
A. 1个B. 2个C. 3个D. 4个
【答案】B
【解析】函数开口向下，
，
函数对称轴在轴左侧，
，
则，
函数图象与轴相交于负半轴，
，
，
故①正确；
该函数图象与轴有2个交点，
，
故②不正确；
，
，
，
，
当时，，
把代入得：，
即，
把点代入得：，即，
，
整理得：，
故③正确；
把代入得：，
抛物线的对称轴是直线，函数图象开口向下，
该函数的顶点坐标为：，即该函数最大值为，
当时，，，
整理得：，即，故④不正确；
综上：正确的有①③，共2个；故选：B．
第Ⅱ卷（非选择题90分）
二、填空题（本大题共6小题，每小题3分，共18分．不需写出解答过程，请将答案直接写在答题卡相应位置上）
11. 如图，以点A为旋转中心，按逆时针方向旋转，得，若，则______．
【答案】
【解析】∵以点A为旋转中心，按逆时针方向旋转，得，
∴，
∴．
故答案为：．
12. 若a，b是方程的两根，则___________．
【答案】2024
【解析】a，b是方程的两根，
，
，
．
故答案：．
13. 若点与点关于原点对称，则抛物线的顶点坐标为______．
【答案】
【解析】∵点与点关于原点对称，
∴，，
∴抛物线解析式为，
∴顶点坐标为，
故答案为：．
14. 在圆柱形油槽内装有一些油，截面如图所示，已知截面半径为，油面宽为，如果再注入一些油后，油面宽变为，则油面上升的高度为______．
【答案】或
【解析】当油面没超过圆心，油面宽为时，
过作于，交于，连接，，
则，
，，
截面半径为，
，
，，
即弦的弦心距是，弦的弦心距是，
则，
即当油面没超过圆心时，油上升了；
当油面超过圆心时，
同理得，
则，
即油面上升了；
故答案为：或．
15. 如图，已知抛物线与直线相交于、B0,3两点，则关于x的不等式的解集是______．
【答案】或
【解析】∵抛物线与直线交于、B0,3两点，
∴由函数图象可得，不等式的解集是或x>0，
故答案为：或x>0．
16. 如图，已知正方形ABCD的边长为2，点M和N分别从B、C同时出发，以相同的速度沿BC、CD方向向终点C和D运动．连接AM，BN交于点P，则PC长的最小值为____________．
【答案】
【解析】由题意得：BM＝CN，
∵四边形ABCD是正方形，
∴∠ABM＝∠BCN＝90°，AB＝BC＝2，
在△ABM和△BCN中，
∵AB＝BC，∠ABM＝∠BCN，MB＝CN，
∴△ABM≌△BCN（SAS），
∴∠BAM＝∠CBN，
∵∠ABP+∠CBN＝90°，
∴∠ABP+∠BAM＝90°，
∴∠APB＝90°，
∴点P在以AB为直径的圆上运动，设圆心为O，运动路径是弧，是这个圆的，如图所示：

连接OC交圆O于P，此时PC最小，
∵AB＝2，
∴OP＝OB＝1，
由勾股定理得：OC＝，
∴PC＝OC﹣OP＝；
故答案为：．
三、解答题（本大题共8小题，满分72分．请在答题卡指定区域内作答，解答时应写出必要的文字说明、证明过程或演算步骤）
17. 解下列方程：
（1）；（2）．
解：（1）原方程可化为：，其中，，，，
，，
解得：，；
（2）原方程化为，去括号，得，
移项合并得，解得：．
18. 如图，已知的三个顶点坐标分别是，，．
（1）请画出与关于原点对称的，并写出点的坐标；
（2）将绕原点顺时针旋转后得到，画出，并写出点的坐标．
解：（1）如图，即为所求，由图可得，点的坐标为；
（2）如图，即为所求，由图可得，点的坐标为．
19. 已知关于x的一元二次方程．
（1）判断该方程实数根的情况；
（2）若实数k及该方程的根均为整数，求k的值．
解：（1）
，
∴该方程总有两个实数根；
（2）设方程的两个根为a、b，
∴，
∵a、b、k都是整数，
∴都是整数，
∴或或．
20. 如图，公路和公路在点P处交汇，且．点A处有一所中学，，一辆行驶速度为的拖拉机从P沿公路前行．
（1）假设拖拉机行驶时周围以内会受到噪声影响，则拖拉机对该中学造成的噪声影响最大时的距离是多少？
（2）该学校受影响的时间为多少？
解：（1）如图所示，过点A作，垂足为B，则就是拖拉机对该中学造成的噪声影响最大时的距离，
∵，，∴，
答：拖拉机对该中学造成的噪声影响最大时的距离为；
（2）以A为圆心，为半径的圆交于C、D两点，连接、，
∴，
在中，
，
∴ ．
，
．
∴受影响的时间为．
21. 打水漂是小伙伴们经常玩的游戏，如图，水漂从水面上（点O）第一次飞起，飞行的最大高度为0.5米，第二次从距离O点4米的A处飞起．据试验，水漂在水面弹起的抛物线与原来的抛物线形状相同，最大高度减少到原来最大高度的一半．
（1）求水漂第二次飞越时，该抛物线的函数表达式；
（2）若此次水漂可以在水面上飞越2次，且第一次击打水面时距离河岸1米，问水漂能否飞过8米宽的河面．
解：（1）由题意，水漂第一次飞越时，飞行的最大高度为0.5米，第二次从距离O点4米的A处飞起．
设水漂第一次飞越时的函数解析式为，
经过点，
，
解得，
水漂第一次飞越时的函数解析式为
水漂在水面弹起的抛物线与原来的抛物线形状相同，最大高度减少到原来最大高度的一半．
设水漂第二次飞越时的函数解析式为，
经过点，
，
解得或（舍去），
水漂第二次飞越时的函数解析式为；
（2）飞越两次，飞越距离，
，
，
总共飞越距离，
，
水漂能不能飞过8米宽的河面．
22. 如图，是的直径，是的切线，，在圆上取一点C，使得，延长、，交点为D．
（1）求证：与相切；
（2）若，求的半径．
解：（1）连接，
∵是的切线，
∴，
∵，，，
∴，
∴，
∵为的半径，
∴与相切；
（2）延长到点，使，连接，，设的半径为，
∵是的切线，
∴，
∵，
∴是线段的垂直平分线，
∴，
∵，
∴，
∴是等边三角形，
∴，
∴，
∴，
∴，
∴，即，
解得，
∴的半径为2．
23. 如图1，已知在正方形中，点E、F分别在边、上运动．
【尝试探究】
（1）如图1，当点E、F分别在边、上运动，时，探究、和的数量关系，并说明理由；
【模型建立】
（2）如图2，当点E、F分别在射线、上运动，时，（1）中的结论是否成立？若成立请加以说明；若不成立，请写出它们的数量关系并加以说明；
【模型应用】
（3）如图3，已知是边长为5的等边三角形，，，以D为顶点作一个60°角，使其角的两边分别交边、于点E、F，连接，求的周长．
解：（1），理由如下：
如图，把绕点顺时针旋转至，可使与重合，
，
，点、、共线，
，，
，
即．
在和中，
，
，
，
；
（2）（1）中的结论不成立．，理由如下：
如图所示．
，
把绕点逆时针旋转至，可使与重合，
，
点、、在一条直线上．
，，．
又，
．
，
．
．
在和中，
，
．
．
，
，
（2）中的结论不成立，、和的数量关系为；
（3）是边长为5的等边三角形，
，，
，
，
，，
把绕点顺时针旋转至，可使与重合，
由旋转得：，，，
，
同理得：点，，在同一条直线上，
，
，
，
，
，，
，
，
，
的周长．
24. 如图1，抛物线与x轴，y轴分别交于，B4,0，C三点．

（1）试求抛物线的解析式；
（2）若P点在第一象限的抛物线上，连接，当的面积最大时，求点P的坐标．
（3）点在第一象限的抛物线上，连接．试问，在对称轴左侧的抛物线上是否存在一点P，满足？如果存在，请求出点P的坐标；如果不存在，请说明理由．
解：（1）把，B4,0，代入，得：
，解得：，
∴；
（2）∵，当时，，
∴，
设直线的解析式为：，
把B4,0，代入，得：，
∴，
过点作轴，交于点，
设，则，

∴，
∴；
∴当时，有最大值，此时；
（3）存在，
∵，
∴抛物线的对称轴为直线，当时，，
∴，
∵，∴轴，，
∵B4,0，∴，
∴，
∵轴，∴，
∴，
设直线与轴交于点，如图，

∵，，，
∴，
∴，
∴，
同（2）可得，直线的解析式为：，
联立，解得：或，
∴．