2024-2025学年山东省济宁市鱼台县九年级(上)10月月考数学试卷(解析版)

这是一份2024-2025学年山东省济宁市鱼台县九年级(上)10月月考数学试卷(解析版)，共12页。试卷主要包含了解答题等内容，欢迎下载使用。
一、单项选择题，精心选一选，相信自己的判断力！（本大题共10小题，每小题3分）
1. 下列是关于x的一元二次方程的是（ ）
A. B.
C. D.
【答案】C
【解析】A、当时，是关于x的一元二次方程，故本选项不符合题意；
B、变形为，则不是关于x的一元二次方程，故本选项不符合题意；
C、是关于x的一元二次方程，故本选项符合题意；
D、不是关于x的一元二次方程，故本选项不符合题意；
故选：C
2. 已知关于x的一元二次方程的常数项为0，则k的值为（ ）
A. -2B. 2C. 2或D. 4或
【答案】A
【解析】根据题意可得：
，
解得．
故选：A．
3. 在平面直角坐标系中，将二次函数的图象向左平移2个单位长度，再向上平移1个单位长度所得抛物线对应的函数表达式为（ ）
A. B.
C. D.
【答案】D
【解析】将二次函数的图象向左平移2个单位长度，得到：
，
再向上平移1个单位长度得到：．
故选：D．
4. 若函数的图象与轴有交点，则的取值范围是（ ）
A. B. 且
C. D. 且
【答案】C
【解析】当时，，图象与轴有一个交点；
当，把代入得，，
∵函数的图象与轴有交点，
∴，
解得；
综上，的取值范围为，
故选：．
5. 一个群里共有x个好友，每个好友都分别给群里的其他好友发一条信息，共发信息420条，则可列方程（ ）
A. B.
C. D.
【答案】D
【解析】根据题意得：．
故选：D．
6. 若二次函数y＝（x-m）2-1，当x≤3时，y随x的增大而减小，则m的取值范围是（ ）
A. m＝3B. m＞3C. m≥3D. m≤3
【答案】C
【解析】二次函数y=（x-m）2-1的对称轴为直线x=m，
∵当x≤3时，y随x的增大而减小，
∴m≥3，故选：C．
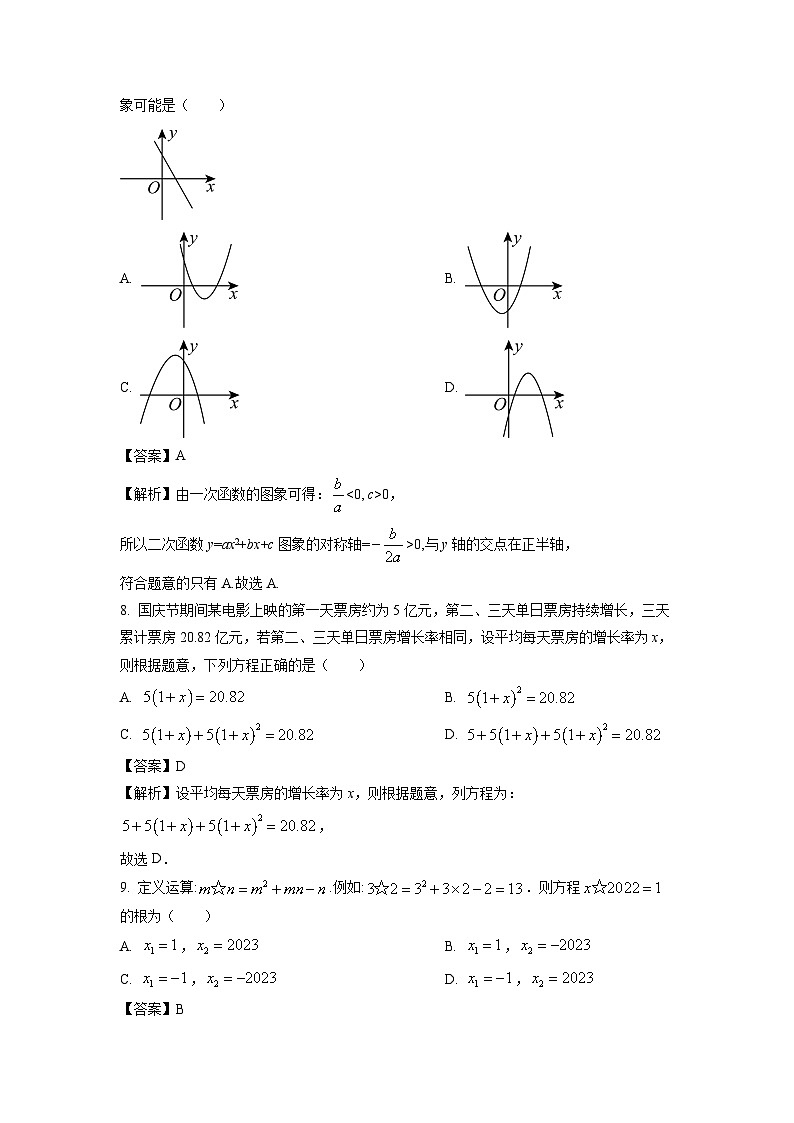
7. 已知一次函数y=x+c的图象如图，则二次函数y=ax2+bx+c在平面直角坐标系中的图象可能是（ ）

A. B.
C. D.
【答案】A
【解析】由一次函数的图象可得：0，
所以二次函数y=ax2+bx+c图象的对称轴=>0,与y轴的交点在正半轴，
符合题意的只有A.故选A.
8. 国庆节期间某电影上映的第一天票房约为5亿元，第二、三天单日票房持续增长，三天累计票房20.82亿元，若第二、三天单日票房增长率相同，设平均每天票房的增长率为x，则根据题意，下列方程正确的是（ ）
A. B.
C. D.
【答案】D
【解析】设平均每天票房的增长率为x，则根据题意，列方程为：
，
故选D．
9. 定义运算:.例如:．则方程的根为（ ）
A. ，B. ，
C. ，D. ，
【答案】B
【解析】∵，
∴，
∴，
∴，
∴，，
解得：，；
故选：B．
10. 二次函数的图象如图所示，下列说法：①；②当或时，；③；④若在该函数的图象上，当时，．⑤其中正确的有（ ）
A. 2个B. 3个C. 4个D. 5个
【答案】B
【解析】∵函数图象的对称轴为：，
，即，故①正确；
由图象可知，当或时，；②错误；
由图象可知，当时，，
，
，
，故③正确；
∵抛物线的对称轴为，开口方向向上，
∴若在函数图象上，
当时，；
当时，；故④错误；
∵，，
∴，故⑤正确；
故选：B．
二、填空题，认真填一填，试一试自己的身手！（本大题共5小题，每小题3分，共15分）
11. 抛物线的顶点坐标是____．
【答案】
【解析】抛物线的顶点的坐标是，
故答案为：．
12. 已知，，是抛物线上的三点，则，，由小到大依序排列是__________．
【答案】
【解析】∵二次函数中，，
∴抛物线开口向上，对称轴为，
∴当时，随的增大而减小；时，随的增大而增大，
∴在对称轴右侧，此时，
∵在对称轴左侧，它关于对称轴对称的点为，且，
，
故答案为：．
13. 已知为方程的根，那么的值为______．
【答案】
【解析】∵a为方程的根，
∴，
∵
，
将代入，则原式，
故答案为：．
14. 已知二次函数的部分图象如图所示，则关于的一元二次不等式的解集为______________________．
【答案】
【解析】由图可知，对称轴为直线x=1，
所以，二次函数图象与x轴的另一个交点坐标为（，0），
由图象可知：函数值大于0的的取值范围为：，
所以，的解集为．
故答案为：．
15. 已知，是关于的一元二次方程的两个不相等的实数根，且满足，则的值是_______________．
【答案】3
【解析】∵方程有两个不相等的实数根，
，
解得：，
依题意得：，
，即，
解得：，
经检验：是原方程的解，
，
，
故答案为：3．
三、解答题（本大题共8小题，16-20题每小题6分，21-22题每小题8分，23题9分，共55分）
16. 解下列方程：
（1）；
（2）
解：（1），
配方得：，
即，
开平方得：，
解得：；
（2），
移项得：，
因式分解得：，
即，
则或，
解得：．
17. 已知二次函数的图象与轴两交点为、．
（1）填空：__________；
（2）求代数式的值．
解：（1）∵二次函数的图象与轴两交点为、，
∴把、代入，
得出，，
故是一元二次方程的解，
则，
∴；
故答案为：5．
（2）依题意，；
则把代入．
18. 已知二次函数．

（1）求该二次函数的顶点坐标；
（2）在平面直角坐标系中，画出二次函数的图象；
（3）结合函数图象，直接写出当时，y的取值范围．
解：（1）∵，
∴该二次函数的顶点坐标为．
（2）把代入，得：
，解得：，
∴该二次函数图象与x轴的交点坐标为或，
把代入得：，
∴该二次函数图象与y轴的交点坐标为；
画出函数图象如图所示：

（3）由图得：当时，．
19. 如图，利用一面墙墙最长可利用米，围成一个矩形花园，与墙平行的一边上要预留米宽的入口（如图中所示，不用砌墙），用砌米长的墙的材料，当矩形的长为多少米时，矩形花园的面积为平方米；能否围成平方米的矩形花园，为什么？

解：设矩形花园的长为x米，则其宽为米，依题意列方程得：
，
，
解这个方程得：，
，
不合题意，舍去，
.
，
，
解这个方程得：，
，
不合题意，都舍去，
答：当矩形长为米时，矩形花园的面积为平方米；不能围成平方米的矩形花园．
20. 已知关于x的一元二次方程,其中a，b，c分别为三边的长．
（1）已知是方程的根，求证：是等腰三角形；
（2）如果是直角三角形，其中，请你判断方程的根的情况，并说明理由．
解：（1）∵是一元二次方程的根，
∴．
∴．
∴是等腰三角形；
（2）方程有两个相等的实数根，理由如下：
∵是直角三角形，其中，
∴．
∴，
∴方程有两个相等的实数根
21. 如图，在平面直角坐标系中，已知点，点、在轴上，并且，动点在过、、三点的抛物线上．
（1）求抛物线的函数表达式；
（2）连接，求三角形面积．
解：（1）∵，
，
，
，
，
设抛物线解析式为，
把代入得，解得，
∴抛物线解析式为，
即．
（2）∵，，
．
22. 据市场调研发现，米工厂今年二月份共生产500个“冰墩墩”，今年四月份共生产720个“冰墩墩”，若该工厂平均每月生产量增加的百分率相同．
（1）求该工厂这两个月的月平均增长率；
（2）已知某商店“冰墩墩”平均每天可销售20个，每个盈利40元，在每个降价幅度不超过10元的情况下，每下降2元，则每天可多售10件．如果每天要盈利1440元，并尽可能的让利于顾客，则每个“冰墩墩”应降价多少元？
解：（1）设该工厂平均每月生产量的增长率为，
依题意得：．
解得（不符合题意，舍去），
答：该工厂这两个月的月平均增长率为．
（2）设每个“冰墩墩”降价元，则每个盈利元，
平均每天可售出个，
依题意得：，
整理得，
解得（不符合题意，舍去）．
则每个“冰墩墩”应降价4元，
答：则每个“冰墩墩”应降价4元．
23. 在平面直角坐标系中,规定:抛物线的“伴随直线”为．
例如：抛物线的“伴随直线”为，即．
（1）在上面规定下，抛物线的顶点坐标为__________，“伴随直线”为__________．
（2）如图，顶点在第一象限的抛物线与其“伴随直线”相交于点，（点在点的左侧），与轴交于点，．若为等腰三角形时，求的值．
解：（1）的顶点坐标为，“伴随直线”为；
故答案为：，；
（2）的伴随直线为，
即，
联立抛物线与伴随直线的解析式可得，
解得或，
，，
在中，令可解得或，
，，
，，
当为等腰三角形时，只存在一种可能为，如图所示，
，即，解得（抛物线开口向下，正值舍去）
若为等腰三角形时，a的值为．