

2025届江苏省宿迁市泗阳县高三(上)期中质量检测数学试卷(解析版)
展开
这是一份2025届江苏省宿迁市泗阳县高三(上)期中质量检测数学试卷(解析版),共16页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 设,,则在复平面内对应的点位于( )
A. 第一象限B. 第二象限
C. 第三象限D. 第四象限
【答案】D
【解析】由,,得,
所以在复平面内对应的点位于第四象限.
故选:D.
2. 若集合,,则( )
A. B.
C. D.
【答案】B
【解析】由题意得,解得,即,
则.
故选:B.
3. 已知向量,满足,,,则( )
A. 2B. C. 4D. 16
【答案】C
【解析】由,得,
而,
因此,所以.
故选:C.
4. 已知是定义在上的奇函数,当时,,若在上单调递减,则的取值范围是( )
A. B.
C. D.
【答案】A
【解析】设,,因为函数的奇函数,所以,
则,
若函数在上单调递减,所以,得.
故选:A.
5. 从5名男生和3名女生中选出4人参加一项创新大赛.如果男生中的甲和女生中的乙至少要有1人在内,那么不同的选法种数为( )
A. 15B. 40C. 55D. 70
【答案】C
【解析】从8名学生中任选4名有种,没有甲乙的选法有种,
所以甲乙至少1人参加的不同的选法种数为.
故选:C.
6. 一个正四棱台油槽可以装汽油190L(1L=1000cm3),若它的上、下底面边长分别为60cm和40cm,则它的深度为( )
A. 25cmB. 75cmC. 100cmD. 150cm
【答案】B
【解析】设四棱台的高为,上底面的面积为,下底面的面积为,
所以,解得:.
故选:B.
7. 当时,函数与的图象有4个交点,则的值为( )
A. 1B. 2C. 3D. 4
【答案】B
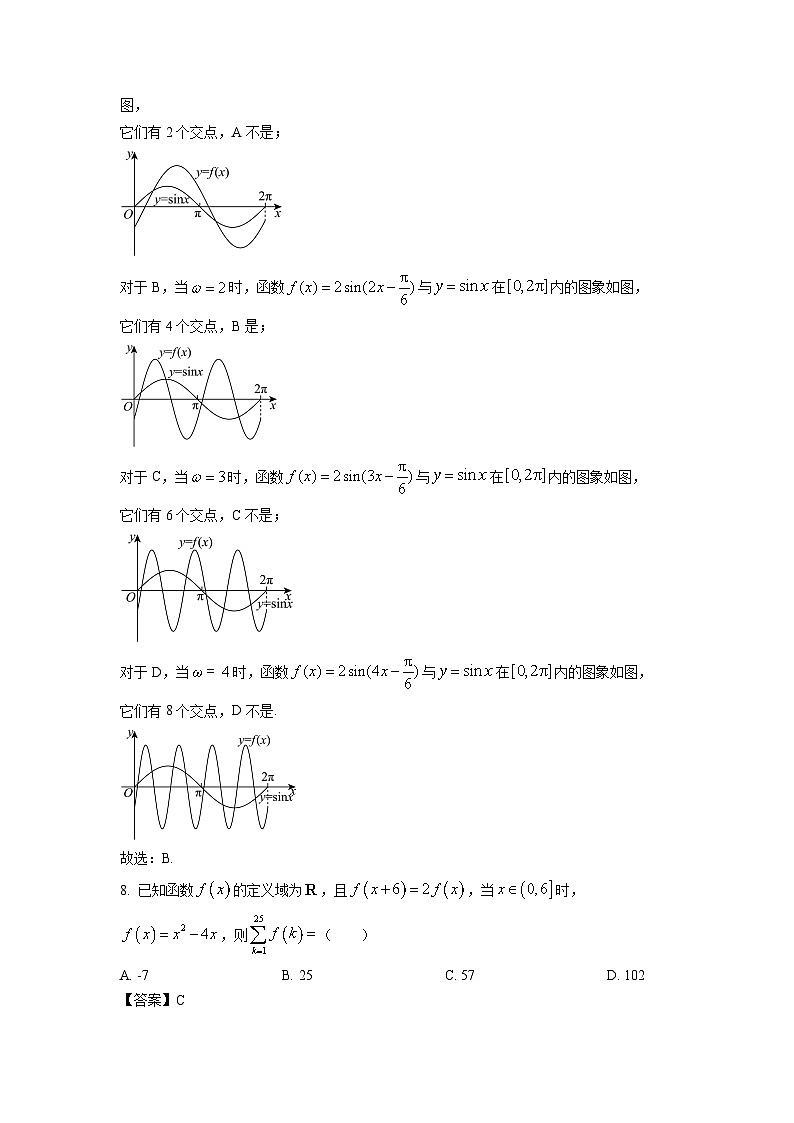
【解析】对于A,当时,函数与在内的图象如图,
它们有2个交点,A不是;
对于B,当时,函数与在内的图象如图,
它们有4个交点,B是;
对于C,当时,函数与在内的图象如图,
它们有6个交点,C不是;
对于D,当时,函数与在内的图象如图,
它们有8个交点,D不是.
故选:B.
8. 已知函数的定义域为,且,当时,,则( )
A. -7B. 25C. 57D. 102
【答案】C
【解析】,
,
.
所以
故选:C.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 在的展开式中,下列说法正确的是( )
A. 的系数为10B. 第4项的二项式系数为10
C. 没有常数项D. 各项系数的和为32
【答案】BC
【解析】展开式第项,
,
对A,令,即时,,的系数为,A错;
对B,第4项的二项式系数,B对;
对C,因,则展开式无常数项,C对;
对D,时,各项系数和不是,则D错,
故选:BC.
10. 在长方体中,,,点P是底面上的一点,且平面,则( )
A. B. 平面
C. 的最小值为D. 的最小值为
【答案】ACD
【解析】A选项,以为坐标原点,所在直线分别为轴,建立空间直角坐标系,
,
则,故,A正确;
B选项,,
所以与不垂直,则平面不成立,B错误;
C选项,设,,
设平面的一个法向量为m=x,y,z,
则,
令得,,所以,
因为平面,所以与垂直,
即,
故,
,
故当时,取得最小值,最小值为,C正确;
D选项,由C选项,,即点在直线上,
由勾股定理得,故四边形为正方形,
将矩形和等腰直角沿着折到同一平面内,如图,
连接,与的交点即为使得最小的点,
最小值为,过点作⊥,交于点,
故,
由勾股定理得,D正确.
故选:ACD.
11. 如图,函数的部分图象,则( )
A.
B. 将图象向右平移后得到函数的图象
C. 在区间上单调递增
D. 在区间上的最大值与最小值之差的取值范围为
【答案】ACD
【解析】对于A,观察图象,,的最小正周期,解得,
由,得,而,则,
所以,A正确;
对于B,将图象向右平移后得到函数,B错误;
对于C,当时,,而正弦函数在上单调递增,
因此在区间上单调递增,C正确.
对于D,函数的图象对称轴为,
当与关于直线对称时,的最大值与最小值的差最小,
此时,,
当为偶数时,,而,
当为奇数时,,而,最大值与最小值的差为1;
当或时,
函数在上单调,最大值与最小值差最大,
,当或时均可取到等号,
所以最大值与最小值之差的取值范围为,D正确.
故选:ACD.
三、填空题:本题共3小题,每小题5分,共15分.
12. 如果随机变量,且,那么________.
【答案】
【解析】由对称性可知,正态密度曲线的对称轴为5,
所以,
所以.
13. 如图,在半径为2、圆心角为的扇形的弧上任取一点A,作扇形的内接平行四边形,使点B在上,点C在上,则该平行四边形面积的最大值为________.
【答案】
【解析】过点分别作分别垂直于点,
则,,又,
所以,所以,
所以平行四边形的面积和长方形的面积相等,
设,,
则,,,
所以,
所以四边形的面积,
所以
,
因为,所以,
故当即时,面积取得最大值为.
14. 已知函数,若,,则正整数a的最小值为______.
【答案】5
【解析】依题意,,当从大于0的方向趋近于0时,函数的值趋近于负无穷大,
而当时,,则必有在上恒成立,
于是且,则,,
求导得,当时,,在上单调递增,
若,即时,,令,
求导得,函数在上单调递减,,即不符合题意;
当,即时,恒成立,则,
令,,
由恒成立,得,
则,又,因此正整数,
又当时,函数在上单调递增,,,符合题意,所以正整数a的最小值为5.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15. 已知函数.
(1)若,求的极值;
(2)若函数的图象关于点对称,求的值.
解:(1)当时,,求导得,
由,可得,得,
则函数在和上单调递增,在上单调递减,
因此当时,有极大值为;
当时,有极小值为.
(2)由函数的图象关于点对称,得,
,
整理得,又,
于是,则,解得,
所以.
16. 在中,A,B,C的对边分别为a,b,c,且满足.
(1)求B;
(2)若四边形内接于圆O,,,求面积的最大值.
解:(1)因为,
所以,
又因为在中,所以,所以,
所以,
所以,即.
因为,所以.
(2)法一:在中,,,所以,
设,则.
所以,,所以,
因为,
所以,
所以
,
所以当,即时面积的最大值为.
法二:在中,已知,
所以,所以,
所以,
所以,(等号当时取得).
所以面积的最大值为.
法三:在四边形的外接圆内考虑,因为,,则,
则的外接圆直径为,
是圆上动点,所以面积取最大值时高最大,即点到距离最大,
此时最大距离为圆心到距离加半径2,
在直角三角形中可知,圆心到距离为,所以高的最大值为,
所以面积的最大值为.
17. 银行储蓄卡的密码由6位数字组成.小明是一位数学爱好者,记得自己随机用了的前6个数字(1,1,3,4,5,9)设置个人银行储蓄卡密码.
(1)求密码中两个1不相邻的概率;
(2)若密码的前三位出现1的次数为X,求X的分布列和数学期望.
解:(1)依题意,的前6个数字的不同排列有种,两个1相邻的有种,
所以密码中两个1不相邻的概率.
(2)依题意,的可能取值为0,1,2,
,,,
所以的分布为:
数学期望.
18. 在四棱锥中,底面是梯形,,,平面平面,,.
(1)求证:;
(2)求与平面所成角的正弦值;
(3)若线段上存在一点E,使得截面将四棱锥分成体积之比为的上下两部分,求点P到截面的距离.
(1)证明:取的中点,连,,由,,得四边形为平行四边形,
由,得平行四边形为矩形,则,
由平面平面,平面平面,平面,得平面
又平面,则,由,,得,
由,,得,则,即,
而,平面,
因此平面,而平面,
所以.
(2)解:由,,,平面,
得平面,平面,则,
以为坐标原点,直线分别为轴建立空间直角坐标系,
则,
,
设平面的法向量,则,
令,得,
设与平面所成角为,,
即与平面所成角的正弦值为.
(3)解:设截面交于,由,面,面,得平面,
又平面,平面平面,则,
依题意,,则,
设,则,
,
,,
到的距离,
截面的面积为,
设平面的法向量m=x,y,z,
则,取,得,
则到平面的距离,
于是,解得,
所以点到截面的距离为.
19. 已知函数及其导函数f'x的定义域都为R,设直线:是曲线的任意一条切线,切点横坐标为,若,当且仅当时“=”成立,则称函数满足“性质”.
(1)判断是否满足“性质”,并说明理由;
(2)若f'x是单调增函数,证明:满足“性质”;
(3)若函数满足“性质”,求实数的取值范围.
解:(1)满足“性质”,理由如下:
因为,设曲线的一条切线切点为,
则直线的方程为:,
因为,
当且仅当时“”成立,
由的任意性可知,满足“性质”.
(2)设直线是曲线的任意一条切线,切点为,
则直线的方程为:,
设,则,
因为是单调增函数,
则当时,,递减,;
当时,,递增,;
即对任意,都有.
由的任意性可知,函数满足“性质”.
(3)①当时,
因为,设,
因为,
所以在上单调递增,即在上单调递增,
由(2)可知,函数满足“性质”.
②下证当时,函数不满足“性质”.
方法一:设直线与曲线切于点,
则直线的方程为:,
设,根据“性质”的定义,要证不满足“性质”,
只要证存在.
因为,
设,则,
设,则递增,且,
所以当时,,递减;
当时,,递增;
因为,,
所以存在,使得,且当时,,
取,则当时,,递减,即递减,
此时,,在上递减,所以,
所以当时,函数不满足“性质”.
综上,实数的取值范围为.
方法2:考虑曲线在处的切线.
,导函数,
在上单调递增,,,
所以存在,使得,
所以时,,单调递减,
又,所以时,,单调递减,
又,所以时,,
即不恒成立,
所以当时,函数不满足“性质”.
综上,实数的取值范围为.0
1
2
相关试卷
这是一份江苏省镇江市2024~2025学年高三(上)期中质量检测数学试卷(含解析),共10页。
这是一份江苏省宿迁市2024~2025学年高三(上)期中数学试卷(含答案),共9页。
这是一份江苏省宿迁市泗阳县2024-2025学年高三上学期期中质量检测数学试题,文件包含高三数学期中试卷终稿与答案pdf、2024-2025学年第一学期高三文化班期中联测数学试卷docx等2份试卷配套教学资源,其中试卷共17页, 欢迎下载使用。









