

广东省湛江市徐闻县多校2024-2025学年七年级数学上学期期中测试卷
展开
这是一份广东省湛江市徐闻县多校2024-2025学年七年级数学上学期期中测试卷,共7页。试卷主要包含了单项选择题,填空题,解答题等内容,欢迎下载使用。
(考试时间:120分钟 满分:120分)
班级:_____________ 姓名:_____________ 得分:_____________
一、单项选择题(本大题共6小题,每小题3分,共18分)
1.如果规定收入为正,支出为负,那么收入2元记作元,支出5元记作( )
A.5元B.元C.元D.7元
2.2024年政府工作报告中提出今年发展主要预期目标之一是城镇新增就业达1200万人以上.数据1200万用科学记数法表示为( )
A.B.C.D.
3.下列各式中,计算正确的是( )
A.B.C.D.
4.数轴上表示数和的点到原点的距离相等,则的值为( )
A.B.2C.1D.
5.下列各式中,计算正确的有( )
①;②;③;④.
A.1个B.2个C.3个D.4个
6.下列图形都是由同样大小的小圆圈按一定规律组成的,其中第①个图形中一共有6个小圆圈,第②个图形中一共有9个小圆圈,第③个图形中一共有12个小圆圈,……按此规律排列,则第⑦个图形中小圆图的个数为( )
A.21B.24C.27D.30
二、填空题(本大题共6小题,每小题3分,共18分)
7.若一个单项式含有字母和,系数是2,次数是3,则这个单项式可以是________(写出一种情况即可).
8.,,且,则的值为________.
9.若多项式的值为5,则多项式的值为________.
10.如图,将刻度尺放在数轴上,若4cm和6cm的刻度分别与数轴上表示1和2的两点对齐,则数轴上与零刻度线对齐的点表示的数为________.
11.有理数,在数轴上对应点的位置如图所示,化简________.
12.如图,按照程序图计算,当输入正整数时,输出的结果是161,则输入的值可能是________________.
三、解答题(本大题共5小题,每小题6分,共30分)
13.(1)计算:;
(2)化简:.
14.化简并求值:,其中.
15.已知,,当,时,求的值.
16.定义一种新的运算“*”,规定有理数,如.求:
(1)的值;
(2)的值.
17.若,的绝对值相等,且,异号,,互为倒数,,是绝对值最小的有理数,求的值.
四、解答题(本大题共3小题,每小题8分,共24分)
18.若多项式与多项式之差的值与字母的取值无关,求的值.
19.小明练习跳绳,以1 min跳165个为目标,并记录20次1 min跳绳的数量如下表(超过165个的部分记为“”,少于165个的部分记为“”):
(1)小明在这20次跳绳练习中,1 min最多跳多少个?
(2)小明在这20次跳绳练习中,1 min跳绳数量最多的一次比最少的一次多多少个?
(3)小明在这20次跳绳练习中,累计跳绳多少个?
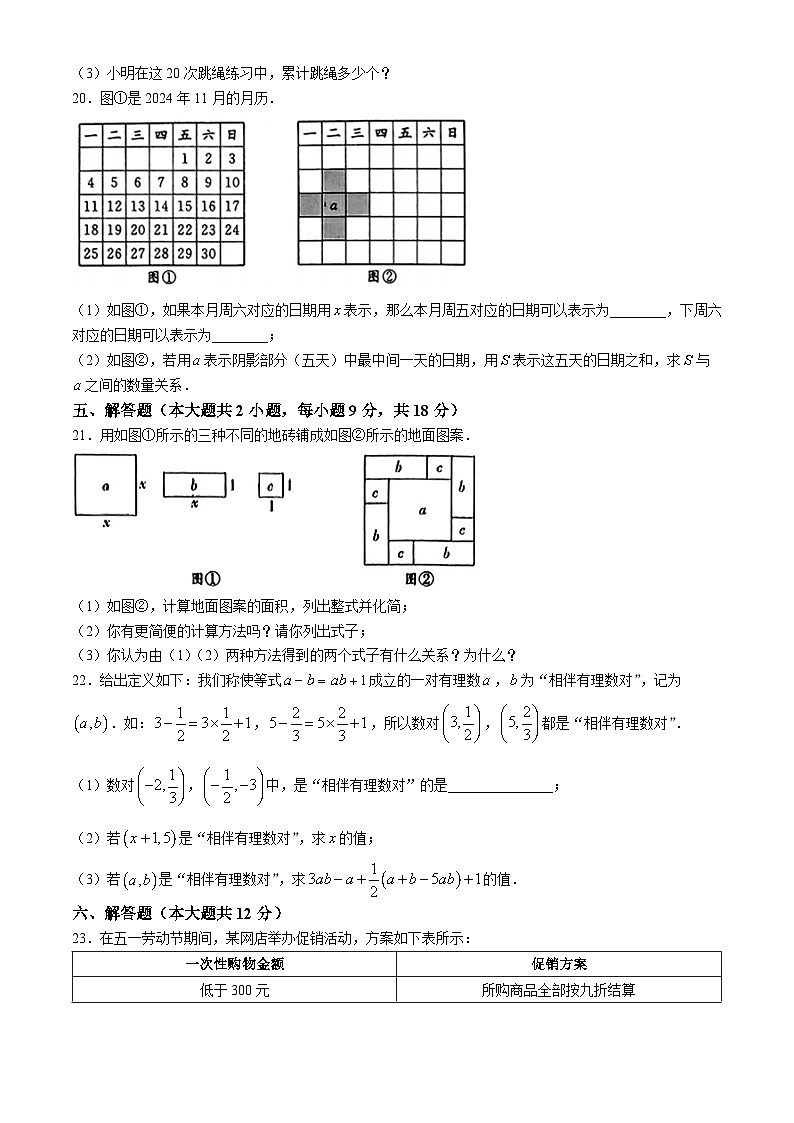
20.图①是2024年11月的月历.
(1)如图①,如果本月周六对应的日期用表示,那么本月周五对应的日期可以表示为________,下周六对应的日期可以表示为________;
(2)如图②,若用表示阴影部分(五天)中最中间一天的日期,用表示这五天的日期之和,求与之间的数量关系.
五、解答题(本大题共2小题,每小题9分,共18分)
21.用如图①所示的三种不同的地砖铺成如图②所示的地面图案.
(1)如图②,计算地面图案的面积,列出整式并化简;
(2)你有更简便的计算方法吗?请你列出式子;
(3)你认为由(1)(2)两种方法得到的两个式子有什么关系?为什么?
22.给出定义如下:我们称使等式成立的一对有理数,为“相伴有理数对”,记为.如:,,所以数对,都是“相伴有理数对”.
(1)数对,中,是“相伴有理数对”的是_______________;
(2)若是“相伴有理数对”,求的值;
(3)若是“相伴有理数对”,求的值.
六、解答题(本大题共12分)
23.在五一劳动节期间,某网店举办促销活动,方案如下表所示:
(1)如果顾客在该网店一次性购物(大于或等于600)元,那么实际付款多少元(用含的式子表示)?
(2)某顾客在该网店两次购物的商品共计800元.若第一次购物的商品的金额为(大于300)元,则该顾客两次购物实际付款多少元(用含的式子表示)?
1.B 2.B 3.D 4.D
5.A【解析】①,故①计算不正确;
②,故②计算不正确;
③,故③计算正确;
④,故④计算不正确.
6.B【解析】第①个图形中一共有(个)小圆圈;
第②个图形中一共有(个)小圆圈;
第③个图形中一共有(个)小圆圈;
……
以此类推,第ⓝ个图形中一共有个小圆圈.
故第⑦个图形中一共有(个)小圆圈.
7.(答案不唯一)
8.0 9.13 10.
11.【解析】由数轴可知,,且,所以.
12.53或17或5或1【解析】如果直接输出结果,那么,解得;
如果两次才输出结果,那么;
如果三次才输出结果,那么;
如果四次才输出结果,那么.
故满足条件的正整数的值可能是53或17或5或1.
13.解:(1)原式
.
(2)原式
.
14.解:原式
.
因为,所以,
所以原式.
15.解:
.
当,时,
原式
.
16.解:(1)因为,
所以
.
(2)
.
17.解:依题意,得,,,,
所以,
所以当时,原式;
当时,原式.
综上所述,原式.
18.解:
.
因为此式的值与的取值无关,所以,,所以,.
故.
19.解:(1)(个).
故小明在这20次跳绳练习中,1 min最多跳175个.
(2)(个).
故小明在这20次跳绳练习中,1 min跳绳数量最多的一次比最少的一次多21个.
(3)(个).
故小明在这20次跳绳练习中,累计跳绳3264个.
20.解:(1)
(2)因为一周有7天,所以阴影部分中上面的日期为,下面的日期为,左边的日期为,右边的日期为,所以.
21.解:(1).
(2)有.
因为铺成的地面图案为正方形,且边长为,所以其面积为.
(3).理由:因为地面图案的面积不变.
22.解:(1)
(2)因为是“相伴有理数对”,
所以,
解得.
(3)原式.
因为,
所以原式.
23.解:(1)当大于或等于600时,实际付款元.
(2)①当大于300且小于或等于500时,大于或等于300且小于500,
两次购物实际付款(元);
②当大于500且小于600时,大于200且小于300,
两次购物实际付款元;
③当大于或等于600且小于800时,大于0且小于或等于200,
两次购物实际付款元.
综上,当大于300且小于或等于500时,两次购物实际付款640元;
当大于500且小于600时,两次购物实际付款元;
当大于或等于600且小于800时,两次购物实际付款元.
与目标数量的差值/个
次数
4
5
3
6
2
一次性购物金额
促销方案
低于300元
所购商品全部按九折结算
低于600元但不低于300元
所购商品全部按八折结算
600元或超过600元
其中前600元按八折结算,
超过600元的部分按七折结算
相关试卷
这是一份广东省茂名市多校2024-2025学年上学期期中七年级数学试题(无答案),共4页。试卷主要包含了单项选择题,填空题,解答题等内容,欢迎下载使用。
这是一份广东省湛江市徐闻县2024—2025学年上学期期中教学调研测试八年级数学试卷,文件包含广东省湛江市徐闻县20242025学年上学期期中教学调研测试八年级数学试卷pdf、八年级数学参考答案docx等2份试卷配套教学资源,其中试卷共8页, 欢迎下载使用。
这是一份[数学][期中]广东省湛江市徐闻县2023-2024学年七年级下学期期中模拟试题(解析版),共12页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。



![[数学][期中]广东省湛江市徐闻县2023-2024学年七年级下学期数学期中试题](http://jx-previews-01.oss-cn-hangzhou.aliyuncs.com/2/3/15924727/0-1719879560231/0.jpg?x-oss-process=image/resize,w_202)





