广东省封开县广信中学2024-2025学年九年级上学期期中考试数学试题

这是一份广东省封开县广信中学2024-2025学年九年级上学期期中考试数学试题，共10页。试卷主要包含了选择题，解答题等内容，欢迎下载使用。
1．下列图形中，既是轴对称图形又是中心对称图形的是（ ）
A．B．C．D．
2．方程化为一般形式后一次项系数和常数项分别是（ ）
A．3，B．，18C．，6D．3，
3．一元二次方程的解是（ ）
A．B．，
C．，D．
4．将抛物线向左平移2个单位后所得抛物线的表达式是（ ）
A．B．C．D．
5．若被击打的小球飞行高度h（单位：m）与飞行时间t（单位：s）具有函数关系为则小球从飞出到落地的所用时间为（ ）
A．3sB．4sC．5sD．6s
6．下列函数关系式中，y是x的二次函数是（ ）
A．B．
C．D．
7．一元二次方程的根的情况是（ ）
A．有两个不相等的实数根B．有两个相等的实数根
C．没有实数根D．无法判断
8．设方程的两个根为，，那么的值等于（ ）
A．B．C．1D．
9．某厂一月份生产空调机1200台，三月份生产空调机1500台，若二、三月份每月平均增长的百分率是x，则所列方程是（ ）
A．B．
C．D．
10．如图，抛物线与x轴交于点，其对称轴为直线，结合图象分析下列结论：①；②；③当时，y随x的增大而增大；④一元二次方程的两根分别为，；⑤若m，为方程的两个根，则且，其中正确的结论有（ ）
A．2个B．3个C．4个D．5个
二、填空题（每小题3分，共18分）
11．在平面直角坐标系中，点关于原点对称的点的坐标是______．
12．将二次函数化成的形式为______．
13．关于x的方程是一元二次方程，则______．
14．如图，将（其中，）绕点A按顺时针方向旋转到的位置，使得点C、A、在同一条直线上，那么旋转角等于______．
15．若m是方程的一个根，则代数式的值等于______．
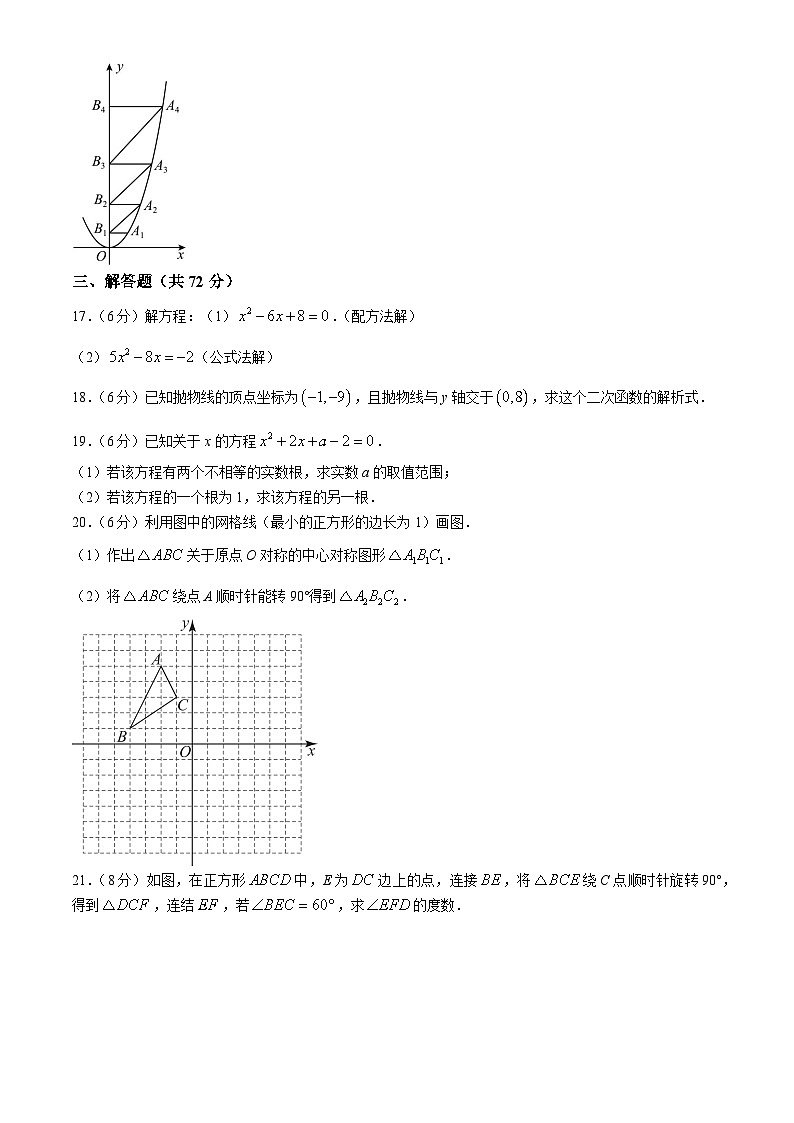
16．抛物线的图象如图所示，点，，，，…，在抛物线第一象限的图象上，点，，，，…，在y轴的正半轴上，、、…、是等腰直角三角形，则______．
三、解答题（共72分）
17．（6分）解方程：（1）．（配方法解）
（2）（公式法解）
18．（6分）已知抛物线的顶点坐标为，且抛物线与y轴交于，求这个二次函数的解析式．
19．（6分）已知关于x的方程．
（1）若该方程有两个不相等的实数根，求实数a的取值范围；
（2）若该方程的一个根为1，求该方程的另一根．
20．（6分）利用图中的网格线（最小的正方形的边长为1）画图．
（1）作出关于原点O对称的中心对称图形．
（2）将绕点A顺时针能转90°得到．
21．（8分）如图，在正方形中，E为边上的点，连接，将绕C点顺时针旋转90°，得到，连结，若，求的度数．
22．（8分）（如图是一块篱笆围成的矩形土地，并且由一条与边平行的篱笆分开，已知篱笆的总长为90米（厚度不计）．设米，米．
（1）用含有x的代数式表示y．
（2）设矩形土地面积为S平方米，当时，求S的最大值．
23．（8分）超市销售某种儿童玩具，如果每件利润为40元（市场管理部门规定，该种玩具每件利润不能超过60元），每天可售出50件．根据市场调查发现，销售单价每增加2元，每天销售量会减少1件．设销售单价增加x元，每天售出y件．
（1）当x为多少时，超市每天销售这种玩具可获利润2250元？
（2）设超市每天销售这种玩具可获利w元，当x为多少时w最大，最大值是多少？
24．（12分）如图，已知抛物线与x轴相交于A、B两点，并与直线交于B、C两点，其中点C是直线与y轴的交点，连接．
（1）求B、C两点坐标以及抛物线的解析式；
（2）证明：为直角三角形；
（3）求抛物线的顶点D的坐标，并求出四边形的面积；
（4）在抛物线的对称轴上有一点P，当周长的最小时，直接写出点P的坐标．
25．（12分）如图①，在中，，，，D为内部的一动点（不在边上），连接，将线段绕点D逆时针旋转60°，使点B到达点F的位置；将线段绕点B顺时针旋转60°，使点A到达点E的位置，连接，，，，，．
（1）求证：；
（2）当取得最小值时，求证：．
（3）如图②，M，N，P分别是，，的中点，连接，，在点D运动的过程中，请判断的大小是否为定值．若是，求出其度数；若不是，请说明理由．
广信中学2024年秋季九年级（上）期中考试数学试卷
参考答案
一、选择题（共30分）
1．D 2．B 3．C 4．A 5．C 6．C 7．A 8．D 9．B 10．B
10．【答案】B
【分析】根据抛物线开口向下和对称轴的位置，抛物线与y轴交于正半轴，可得：，，，即可判断①；由，结合：，，即可判断②；根据抛物线开口向下，对称轴为直线，即可判断③；由的两根是：，，得：的两根是：，，进而得：的两根，即可判断④；由m，为方程的两个根，得：m，为抛物线和直线的两个交点的横坐标，结合图象，即可得到m，n的范围，即可判断⑤．
【详解】∵抛物线开口向下，∴，
∵对称轴为：直线，∴，即：，∴，
∵抛物线与y轴交于正半轴，∴，∴，故①正确；
∵抛物线与x轴交于点，∴，
∵，∴，∴，故②正确；
∵当时，y随x的增大而增大，当时，y随x的增大而减小，故③错误；
∵抛物线与x轴交于点，其对称轴为直线，
∴抛物线与x轴交于点和，
∴的两根是：，，
∴的两根是：，，
∵与的解相同，
∴的两根分别为，，故④正确；
∵抛物线与x轴交于点和，
∴，
∵m，为方程的两个根，
∴m，为方程的两个根，
∴m，为抛物线和直线的两个交点的横坐标，
结合图象得：且，故⑤错误；故选B．
【点睛】本题主要考查二次函数的图象性质与一元二次方程的综合，理解函数的图象交点的横坐标与方程的根的关系，是解题的关键，体现了数形结合的思想方法．
二、填空题（共18分）
11．略 12．略 13．略 14．略 15．略
16．【答案】
【分析】先设第一个等腰直角三角形的直角边长为x，表示出点的坐标，代入二次函数的解析式，求出x；设第二个等腰直角三角形的直角边长为m，表示出的坐标，代入二次函数的解析式，求出m，同理求出第2022个等腰直角三角形的直角边长，即可求出斜边．
【详解】解：设，∵是等腰直角三角形，∴，
则的坐标为，代入二次函数，得，解得或（舍），
设，∵腰是等腰直角三角形，
∴，∴的坐标为，
代入二次函数，得，
解得或（舍），同理可求出，，
∴，根据勾股定理，得，故答案为：．
【点睛】本题考查了二次函数图象与规律综合题，利用等腰直角三角形的性质和二次函数的点坐标特征是解决本题的关键．
三、解答题（共72分）
17．（4分）【详解】解：，
∴，∴，
∴或，解得：，．
18．【详解】解：由抛物线顶点坐标为可设其解析式为，
将代入，得：，解得：，
则抛物线解析式为．
19．略 20．略
21．【详解】解：∵将绕点C顺时针方向旋转90°得到，
∴，∴，，
∵四边形是正方形，
∴，∴，
∵，∴，
∴．
22．（本题满分10分）
解：（1）由题意可得，，；
（2），
∵，开口向下，∴当时，
∴对称轴不在范围内
∴当时，S取得最大值，．
23．【详解】（1）根据题意得，，
解得：，，
∵每件利润不能超过60元，∴，
答：当x为10时，超市每天销售这种玩具可获利润2250元；
（2）根据题意得，，
∵，∴当时，w随x的增大而增大，
∴当时，，
答：当x为20时w最大，最大值是2400元．
【点睛】本题考查了一元二次方程、二次函数的应用，根据的数量关系列出方程或二次函数解析式是解题关键．
24．【详解】（1）解：在直线中，当时，，当时，，
∴，，
∵抛物线经过点和点，
∴，解得
∴抛物线的解析式为．
（2）证明：在中，当时，则，
解得，，∴．
∵，，∴，，，∴，即．
∵，
∴，，
∴，∴，
∴是直角三角形；
（3）解：∵抛物线解析式为，
∴抛物线的顶点D的坐标是；
如图1，连接，
∴，
∴四边形的面积是．
（4）解：∵抛物线解析式为，
∴抛物线的对称轴为．
如图2，设抛物线的对称轴与直线交于点E，
点P是直线上的点，连接，．
∵垂直平分，∴，，∴．
∵为定值，∴当的值最小时，的周长最小．
∵，
∴当点P与点E重合时，，
∴此时最小，
∵直线，当时，，∴，
∴当的周长最小时，点P的坐标为．
【点睛】此题重点考查一次函数的图象与性质、二次函数的图象与性质、用待定系数法求函数关系式、勾股定理及其逆定理的应用、轴对称的性质、两点之间线段最短等知识与方法，此题综合性强，难度较大，属于考试压轴题．
25．（1）见详解；（2）见详解；（3），理由见详解
【分析】（1）由旋转60°知，、、，故由证出全等即可；
（2）由题意可知为等边三角形得，再由C、D、F、E共线时最小，，最后，即证；
（3）由中位线定理知道，，，，由得，即，再设，，则，，得，得．
【详解】（1）证明：∵，∴，∴，
在与中，∴；
（2）证明：∵，，∴为等边三角形，即，
∵C、D、F、E共线时最小，∴，
∵，∴，
∴，
∴，∴；
（3）的大小是为定值，理由：如图，连接，
∵M，N，P分别是，，的中点，
∴,,，，
∵，∴，∴，
∵且，∴为等边三角形，
设，，
则，，
∴，，
∴，
∴．