广东省茂名市化州市2024-2025学年九年级上学期期中数学试卷

这是一份广东省茂名市化州市2024-2025学年九年级上学期期中数学试卷，共22页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．（3分）下列说法正确的是（ ）
A．菱形的四个内角都是直角
B．矩形的对角线互相垂直
C．正方形的每一条对角线平分一组对角
D．平行四边形是轴对称图形
2．（3分）一元二次方程x2＝2x的两根分别为（ ）
A．x1＝x2＝0B．x1＝x2＝4
C．x1＝2，x2＝﹣2D．x1＝0，x2＝2
3．（3分）下列说法中，不正确的是（ ）
A．“a是实数，|a|≥0”是必然事件
B．任意掷一枚质地均匀的硬币100次，正面朝上的次数一定是50次
C．通过大量重复试验，可以用频率估计概率
D．不可能事件发生的概率为0
4．（3分）已知关于x的一元二次方程（a﹣1）x2+x+a2﹣1＝0的常数项是0，则a的值为（ ）
A．1B．﹣1C．1或﹣1D．
5．（3分）如图，将四根木条用钉子钉成一个矩形框架ABCD，然后向右扭动框架，观察所得四边形的变化．下列判断错误的是（ ）
A．四边形ABCD由矩形变为平行四边形
B．对角线BD的长度变大
C．四边形ABCD的面积不变
D．四边形ABCD的周长不变
6．（3分）小冰和小雪自愿参加学校组织的课后托管服务活动，随机选择自主阅读、体育活动、科普活动三项中的某一项，那么小冰和小雪同时选择“体育活动”的概率为（ ）
A．B．C．D．
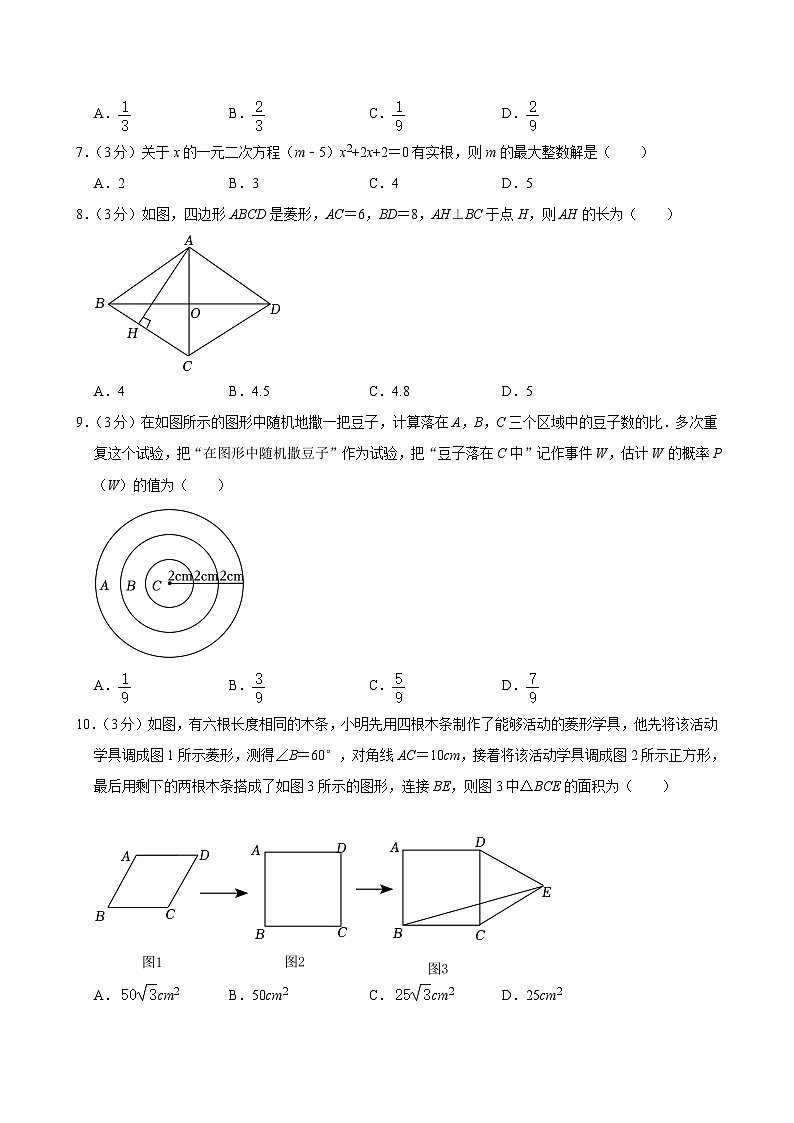
7．（3分）关于x的一元二次方程（m﹣5）x2+2x+2＝0有实根，则m的最大整数解是（ ）
A．2B．3C．4D．5
8．（3分）如图，四边形ABCD是菱形，AC＝6，BD＝8，AH⊥BC于点H，则AH的长为（ ）
A．4B．4.5C．4.8D．5
9．（3分）在如图所示的图形中随机地撒一把豆子，计算落在A，B，C三个区域中的豆子数的比．多次重复这个试验，把“在图形中随机撒豆子”作为试验，把“豆子落在C中”记作事件W，估计W的概率P（W）的值为（ ）
A．B．C．D．
10．（3分）如图，有六根长度相同的木条，小明先用四根木条制作了能够活动的菱形学具，他先将该活动学具调成图1所示菱形，测得∠B＝60°，对角线AC＝10cm，接着将该活动学具调成图2所示正方形，最后用剩下的两根木条搭成了如图3所示的图形，连接BE，则图3中△BCE的面积为（ ）
A．cm2B．50cm2C．cm2D．25cm2
二、填空题（本大题共5小题，每小题3分，共15分，请将下列各题的正确答案写在答题卡相应的位置上）
11．（3分）一元二次方程x2﹣4x+3＝0配方为（x﹣2）2＝k，则k的值是 ．
12．（3分）一个盒子中装有20颗蓝色幸运星，若干颗红色幸运星和15颗黄色幸运星，小明通过多次摸取幸运星试验后发现，摸取到红色幸运星的频率稳定在0.5左右，则红色幸运星颗数约为 颗．
13．（3分）已知关于x的一元二次方程ax2+bx+6＝0的一个根是3，则3a+b＝ ．
14．（3分）菱形ABCD的对角线AC＝12，S菱形ABCD＝48，则AB的长为 ．
15．（3分）如图，四边形ABCD，CEFG均为正方形，其中正方形CEFG的面积为36cm2，若图中阴影部分的面积为10cm2，则正方形ABCD的面积为 cm2．
三、解答题（一）：本大题共3小题，每小题7分，满分21分，解答应写出文字说明、证明过程或演算步骤。
16．（7分）解方程：x2+4x﹣1＝0．
17．（7分）2023年9月23日，第19届亚运会在杭州开幕，电子竞技首次成为亚运会正式比赛项目．小明和小张是电竞游戏的爱好者，他们相约一起去现场为中国队加油，现场的观赛区分为A、B、C、D四个区域，购票以后系统随机分配观赛区域．
（1）小明购买门票在A区观赛的概率为 ；
（2）求小明和小张在同一区域观看比赛的概率．（请用画树状图或列表等方法说明理由）
18．（7分）如图，一块长和宽分别为60厘米和40厘米的长方形铁皮，要在它的四角截去四个相等的小正方形，折成一个无盖的长方体水槽，使它的底面积为800平方厘米，求截去正方形的边长．
四、解答题（二）：本大题共3小题，每小题9分，满分27分，解答应写出文字说明、证明过程或演算步骤。
19．（9分）已知关于x的一元二次方程x2+2mx+m2﹣3＝0．
（1）求证：无论m为何值，该方程总有两个不相等的实数根；
（2）若该方程的两个根为p和q，且满足pq﹣p﹣q＝0，求m的值．
20．（9分）为落实“双减提质”，进一步深化“数学提升工程”，提升学生数学核心素养，某学校拟开展“双减”背景下的初中数学活动型作业成果展示现场会，为了解学生最喜爱的项目，现随机抽取若干名学生进行调查，并将调查结果绘制成如所示两幅不完整的统计图：
根据以上信息，解答下列问题：
（1）参与此次抽样调查的学生人数是 人，补全统计图①（要求在条形图上方注明人数）；
（2）计划在A，B，C，D，E五项活动中随机选取两项作为直播项目，请用列表或画树状图的方法，求恰好选中B，E这两项活动的概率．
21．（9分）如图所示，点O是菱形ABCD对角线的交点，CE∥BD，EB∥AC，连接OE，交BC于F．
（1）求证：四边形OCEB是矩形；
（2）如果设AC＝12，BD＝16，求OE的长．
五、解答题（三）：本大题共2小题，第22题13分，第23题14分，满分27分，解答应写出文字说明、证明过程或演算步骤。
22．（13分）解决问题：邓州公安交警部门提醒市民，骑车出行必须严格遵守“一盔一带”的规定．某头盔经销商统计了某品牌头盔7月份到9月份的销量，该品牌头盔7月份销售500个，9月份销售720个，且从7月份到9月份销售量的月增长率相同．
（1）求该品牌头盔销售量的月增长率；
（2）若此种头盔的进价为30元/个，经市场预测，当售价为40元/个时，月销售量为600个，若在此基础上售价每上涨1元/个，则月销售量将减少10个，为使月销售利润达到10000元，而且尽可能让顾客得到实惠，该品牌头盔的实际售价应定为多少元？
23．（14分）如图，正方形ABCD中，点E、M、N分别在AB、AD、BC上，DE与MN相交于点O，记∠MOD＝α．
（1）如图1，若∠MOD＝90°，求证：DE＝MN；
（2）如图2，若∠MOD＝45°，边长AB＝4，MN＝，求线段DE的长．
2024-2025学年广东省茂名市化州市九年级（上）期中数学试卷
参考答案与试题解析
一、选择题（本大题共10小题，每小题3分，共30分，在每小题给出四个选项中，其中只有一个是正确的，把选出的答案填涂在答题卡上）
1．（3分）下列说法正确的是（ ）
A．菱形的四个内角都是直角
B．矩形的对角线互相垂直
C．正方形的每一条对角线平分一组对角
D．平行四边形是轴对称图形
【答案】C
【分析】根据菱形、矩形、正方形、平行四边形的性质和轴对称图形的性质即可求解．
【解答】解：A．菱形的四个内角不一定都是直角，故A选项不符合题意；
B．矩形的对角线不一定互相垂直，故B选项不符合题意；
C．正方形的每一条对角线平分一组对角，故C选项符合题意；
D．平行四边形不一定是轴对称图形，故D选项不符合题意；
故选：C．
【点评】本题考查了菱形的性质、矩形的性质、正方形的性质、平行四边形和轴对称图形的性质，解题的关键是逐个判断四个选项即可得出正确答案．
2．（3分）一元二次方程x2＝2x的两根分别为（ ）
A．x1＝x2＝0B．x1＝x2＝4
C．x1＝2，x2＝﹣2D．x1＝0，x2＝2
【答案】D
【分析】利用因式分解法求解可得．
【解答】解：x2＝2x，
x2﹣2x＝0，
∴x（x﹣2）＝0，
∴x＝0或x﹣2＝0，
解得x1＝0，x2＝2．
故选：D．
【点评】本题主要考查解一元二次方程的能力，熟练掌握解一元二次方程的几种常用方法：直接开平方法、因式分解法、公式法、配方法，结合方程的特点选择合适、简便的方法是解题的关键．
3．（3分）下列说法中，不正确的是（ ）
A．“a是实数，|a|≥0”是必然事件
B．任意掷一枚质地均匀的硬币100次，正面朝上的次数一定是50次
C．通过大量重复试验，可以用频率估计概率
D．不可能事件发生的概率为0
【答案】B
【分析】根据随机事件，概率的意义，利用频率估计概率逐一判断即可解答．
【解答】解：A、“a是实数，|a|≥0”是必然事件，故A不符合题意；
B、任意掷一枚质地均匀的硬币100次，正面朝上的次数不一定是50次，故B符合题意；
C、通过大量重复试验，可以用频率估计概率，故C不符合题意；
D、不可能事件发生的概率为0，故D不符合题意；
故选：B．
【点评】本题考查了随机事件，概率的意义，利用频率估计概率，熟练掌握这些数学知识是解题的关键．
4．（3分）已知关于x的一元二次方程（a﹣1）x2+x+a2﹣1＝0的常数项是0，则a的值为（ ）
A．1B．﹣1C．1或﹣1D．
【答案】B
【分析】根据一元二次方程的定义和题意列出a满足的条件求解即可．
【解答】解：由题意，，
解得：a＝﹣1，
故选：B．
【点评】本题考查一元二次方程的定义和解法，掌握一元二次方程的定义与基本解法是解题关键．
5．（3分）如图，将四根木条用钉子钉成一个矩形框架ABCD，然后向右扭动框架，观察所得四边形的变化．下列判断错误的是（ ）
A．四边形ABCD由矩形变为平行四边形
B．对角线BD的长度变大
C．四边形ABCD的面积不变
D．四边形ABCD的周长不变
【答案】C
【分析】由题意可知向右扭动矩形框架ABCD，四边形变成平行四边形，四边形的四条边不变，故周长不变，对角线BD减小，但是BC边上的高减小，故面积变小，故选C．
【解答】解：向右扭动矩形框架ABCD，只改变四边形的形状，四边形变成平行四边形，A不符合题意；
此时对角线BD减小，对角线AC增大，B不合题意．
BC边上的高减小，故面积变小，C符合题意，
四边形的四条边不变，故周长不变，D不符合题意．
故选：C．
【点评】本题考查矩形的性质和平行四边形的性质，熟悉性质是解题关键．
6．（3分）小冰和小雪自愿参加学校组织的课后托管服务活动，随机选择自主阅读、体育活动、科普活动三项中的某一项，那么小冰和小雪同时选择“体育活动”的概率为（ ）
A．B．C．D．
【答案】C
【分析】画树状图，共有9种等可能的结果，其中小冰和小雪同时选择“体育活动”的结果有1种，再由概率公式求解即可．
【解答】解：设自主阅读、体育活动、科普活动分别记为A、B、C，
画树状图如下：
共有9种等可能的结果，其中小冰和小雪同时选择“体育活动”的结果有1种，
∴小冰和小雪同时选择“体育活动”的概率为，
故选：C．
【点评】本题考查了用树状图法求概率，树状图法可以不重复不遗漏的列出所有可能的结果，适合两步或两步以上完成的事件，解题时要注意此题是放回试验还是不放回试验．用到的知识点为：概率＝所求情况数与总情况数之比．
7．（3分）关于x的一元二次方程（m﹣5）x2+2x+2＝0有实根，则m的最大整数解是（ ）
A．2B．3C．4D．5
【答案】C
【分析】根据方程有实数根得出△≥0且m﹣5≠0，求出不等式的解集即可．
【解答】解：∵关于x的一元二次方程（m﹣5）x2+2x+2＝0有实根，
∴Δ＝22﹣4（m﹣5）×2≥0且m﹣5≠0，
解得：m≤5.5且m≠5，
m的最大整数解为4，
故选：C．
【点评】本题考查了根的判别式和解一元一次不等式，能得出关于m的不等式是解此题的关键．
8．（3分）如图，四边形ABCD是菱形，AC＝6，BD＝8，AH⊥BC于点H，则AH的长为（ ）
A．4B．4.5C．4.8D．5
【答案】C
【分析】根据菱形的性质得出BO、CO的长，在Rt△BOC中求出BC，利用菱形面积等于对角线乘积的一半，也等于BC×AH，即可得出AH的长度．
【解答】解：∵四边形ABCD是菱形，
∴CO＝AC＝3，BO＝BD＝4，AO⊥BO，
∴BC＝5，
∴S菱形ABCD＝AC•BD＝×6×8＝24，
∵S菱形ABCD＝BC×AH，
∴BC×AH＝24，
∴AH＝＝4.8，
故选：C．
【点评】本题考查了菱形的性质，也涉及了勾股定理，要求我们掌握菱形的面积的两种表示方法，及菱形的对角线互相垂直且平分．
9．（3分）在如图所示的图形中随机地撒一把豆子，计算落在A，B，C三个区域中的豆子数的比．多次重复这个试验，把“在图形中随机撒豆子”作为试验，把“豆子落在C中”记作事件W，估计W的概率P（W）的值为（ ）
A．B．C．D．
【答案】A
【分析】落在A，B，C三个区域中的豆子数的比等于A，B，C的面积比．利用面积比估计概率即可．
【解答】解：根据题意得：豆子落在C中”记作事件A，估计A的概率P（A）的值＝．
故选：A．
【点评】本题考查利用频率估计概率，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．
10．（3分）如图，有六根长度相同的木条，小明先用四根木条制作了能够活动的菱形学具，他先将该活动学具调成图1所示菱形，测得∠B＝60°，对角线AC＝10cm，接着将该活动学具调成图2所示正方形，最后用剩下的两根木条搭成了如图3所示的图形，连接BE，则图3中△BCE的面积为（ ）
A．cm2B．50cm2C．cm2D．25cm2
【答案】D
【分析】根据菱形的性质可知BC＝10cm，过点E作EH⊥BC，交BC的延长线于点H，根据等边三角形的性质可知∠ECH＝30°，根据含30°角的直角三角形的性质可得EH的长，再根据△BCE的面积＝求解即可．
【解答】解：
图1连接AC，
∵菱形ABCD中，AB＝BC，
∵∠B＝60°，
∴△ABC是等边三角形，
∵对角线AC＝10cm，
∴BC＝10cm，
∴CE＝BC＝10cm，
图3过点E作EH⊥BC，交BC的延长线于点H，
∵△DCE是等边三角形，
∴∠DCE＝60°，
∴∠ECH＝30°，
∴EH＝CE＝5cm，
∴△BCE的面积＝＝＝25（cm2），
故选：D．
【点评】本题考查了正方形的性质，菱形的性质，等边三角形的性质，含30°角的直角三角形的性质，三角形的面积等，熟练掌握这些性质是解题的关键．
二、填空题（本大题共5小题，每小题3分，共15分，请将下列各题的正确答案写在答题卡相应的位置上）
11．（3分）一元二次方程x2﹣4x+3＝0配方为（x﹣2）2＝k，则k的值是 1 ．
【答案】见试题解答内容
【分析】根据配方法可以将题目中方程变形，然后即可得到k的值．
【解答】解：∵x2﹣4x+3＝0，
∴x2﹣4x＝﹣3，
∴x2﹣4x+4＝﹣3+4，
∴（x﹣2）2＝1，
∵一元二次方程x2﹣4x+3＝0配方为（x﹣2）2＝k，
∴k＝1，
故答案为：1．
【点评】本题考查解一元二次方程—配方法，解答本题的关键是明确题意，会用配方法将方程变形．
12．（3分）一个盒子中装有20颗蓝色幸运星，若干颗红色幸运星和15颗黄色幸运星，小明通过多次摸取幸运星试验后发现，摸取到红色幸运星的频率稳定在0.5左右，则红色幸运星颗数约为 35 颗．
【答案】见试题解答内容
【分析】设袋中红色幸运星有x颗，根据“摸取到红色幸运星的概率稳定在0.5左右”列出关于x的方程，解之可得袋中红色幸运星的个数．
【解答】解：设袋中红色幸运星有x颗，
根据题意，得：，
解得：x＝35，
经检验：x＝35是原分式方程的解，
故答案为：35．
【点评】本题主要考查了已知概率求相关数量，正确列出方程是解题的关键．
13．（3分）已知关于x的一元二次方程ax2+bx+6＝0的一个根是3，则3a+b＝ ﹣2 ．
【答案】见试题解答内容
【分析】把x＝3代入关于x的一元二次方程ax2+bx+6＝0得关于a，b的等式，再根据等式的基本性质进行变形即可．
【解答】解：把x＝3代入关于x的一元二次方程ax2+bx+6＝0得：9a+3b+6＝0，
9a+3b＝﹣6，
∴3a+b＝﹣2，
故答案为：﹣2．
【点评】本题主要考查了一元二次方程的解，解题关键是熟练掌握一元二次方程的解是使方程左右两边相等的未知数的值．
14．（3分）菱形ABCD的对角线AC＝12，S菱形ABCD＝48，则AB的长为 ．
【答案】．
【分析】利用菱形的面积公式求出BD＝8，利用菱形的性质得到∠AOB＝90°，，，利用勾股定理求出AB的长即可．
【解答】解：如图，
，
∵AC＝12，S菱形ABCD＝48，
∴，
∴BD＝8，
∵四边形ABCD是菱形，
∴，，AC⊥BD，
∴，
故答案为：．
【点评】本题主要考查了菱形的性质，勾股定理，熟知菱形的性质是解题的关键．
15．（3分）如图，四边形ABCD，CEFG均为正方形，其中正方形CEFG的面积为36cm2，若图中阴影部分的面积为10cm2，则正方形ABCD的面积为 16 cm2．
【答案】见试题解答内容
【分析】由四边形ABCD为正方形，正方形CEFG的面积为36cm2，得CE＝6 cm，设CD＝x cm，DE＝（6﹣x）cm，由阴影部分的面积为10cm2，得（6﹣x）•（6+x）＝10，即可得正方形ABCD的面积＝x2＝16cm2．
【解答】解：由四边形ABCD为正方形，正方形CEFG的面积为36cm2，
得CE＝6 cm，设CD＝x cm，DE＝（6﹣x）cm，
由阴影部分的面积为10cm2，
得（6﹣x）•（6+x）＝10，
得正方形ABCD的面积＝x2＝16cm2．
故答案为：16．
【点评】本题主要考查了正方形中面积的计算，解题关键是面积公式的正确应用．
三、解答题（一）：本大题共3小题，每小题7分，满分21分，解答应写出文字说明、证明过程或演算步骤。
16．（7分）解方程：x2+4x﹣1＝0．
【答案】见试题解答内容
【分析】首先进行移项，得到x2+4x＝1，方程左右两边同时加上4，则方程左边就是完全平方式，右边是常数的形式，再利用直接开平方法即可求解．
【解答】解：∵x2+4x﹣1＝0
∴x2+4x＝1
∴x2+4x+4＝1+4
∴（x+2）2＝5
∴x＝﹣2±
∴x1＝﹣2+，x2＝﹣2﹣．
【点评】配方法的一般步骤：
（1）把常数项移到等号的右边；
（2）把二次项的系数化为1；
（3）等式两边同时加上一次项系数一半的平方．
选择用配方法解一元二次方程时，最好使方程的二次项的系数为1，一次项的系数是2的倍数．
17．（7分）2023年9月23日，第19届亚运会在杭州开幕，电子竞技首次成为亚运会正式比赛项目．小明和小张是电竞游戏的爱好者，他们相约一起去现场为中国队加油，现场的观赛区分为A、B、C、D四个区域，购票以后系统随机分配观赛区域．
（1）小明购买门票在A区观赛的概率为 ；
（2）求小明和小张在同一区域观看比赛的概率．（请用画树状图或列表等方法说明理由）
【答案】见试题解答内容
【分析】（1）直接利用概率公式可得答案．
（2）画树状图得出所有等可能的结果数以及小明和小张在同一区域观看比赛的结果数，再利用概率公式可得出答案．
【解答】解：（1）由题意得，小明购买门票在A区观赛的概率为．
故答案为：．
（2）画树状图如下：
共有16种等可能的结果，其中小明和小张在同一区域观看比赛的结果有4种，
∴小明和小张在同一区域观看比赛的概率为＝．
【点评】本题考查列表法与树状图法、概率公式，熟练掌握列表法与树状图法以及概率公式是解答本题的关键．
18．（7分）如图，一块长和宽分别为60厘米和40厘米的长方形铁皮，要在它的四角截去四个相等的小正方形，折成一个无盖的长方体水槽，使它的底面积为800平方厘米，求截去正方形的边长．
【答案】见试题解答内容
【分析】可设截去正方形的边长为x厘米，对于该长方形铁皮，四个角各截去一个边长为x厘米的小正方形，长方体底面的长和宽分别是：（60﹣2x）厘米和（40﹣2x）厘米，底面积为：（60﹣2x）（40﹣2x），现在要求长方体的底面积为：800平方厘米，令二者相等求出x的值即可．
【解答】解：设截去正方形的边长为x厘米，由题意得，长方体底面的长和宽分别是：（60﹣2x）厘米和（40﹣2x）厘米，
所以长方体的底面积为：（60﹣2x）（40﹣2x）＝800，
即：x2﹣50x+400＝0，
解得x1＝10，x2＝40（不合题意舍去）．
答：截去正方形的边长为10厘米．
【点评】此题考查了一元二次方程的应用，本题的关键在于理解题意，找出等量关系：底面积为800平方厘米，列出方程求解即可．
四、解答题（二）：本大题共3小题，每小题9分，满分27分，解答应写出文字说明、证明过程或演算步骤。
19．（9分）已知关于x的一元二次方程x2+2mx+m2﹣3＝0．
（1）求证：无论m为何值，该方程总有两个不相等的实数根；
（2）若该方程的两个根为p和q，且满足pq﹣p﹣q＝0，求m的值．
【答案】（1）证明详见解析；
（2）m的值为1或﹣3．
【分析】（1）先计算Δ＝b2﹣4ac＝12＞0，从而可得结论；
（2）由根与系数的关系可得p+q＝﹣2m，pq＝m2﹣3，再代入pq﹣p﹣q＝0，建立方程求解即可．
【解答】（1）证明：∵Δ＝b2﹣4ac＝4m2﹣4（m2﹣3）＝12＞0，
∴无论m为何值，该方程总有两个不相等的实数根．
（2）解：由根与系数的关系，得p+q＝﹣2m，pq＝m2﹣3，
∵pq﹣p﹣q＝0，
∴m2﹣3+2m＝0，
即m2+2m﹣3＝0，
解得：m1＝1，m2＝﹣3，
∴m的值为：1或﹣3．
【点评】本题考查的一元二次方程根的判别式，一元二次方程根与系数的关系，熟知以上知识是解题的关键．
20．（9分）为落实“双减提质”，进一步深化“数学提升工程”，提升学生数学核心素养，某学校拟开展“双减”背景下的初中数学活动型作业成果展示现场会，为了解学生最喜爱的项目，现随机抽取若干名学生进行调查，并将调查结果绘制成如所示两幅不完整的统计图：
根据以上信息，解答下列问题：
（1）参与此次抽样调查的学生人数是 120 人，补全统计图①（要求在条形图上方注明人数）；
（2）计划在A，B，C，D，E五项活动中随机选取两项作为直播项目，请用列表或画树状图的方法，求恰好选中B，E这两项活动的概率．
【答案】（1）120；补全统计图见解答过程；
（2）．
【分析】（1）用条形统计图中B的人数除以扇形统计图中B的百分比可得参与此次抽样调查的学生人数；求出选择E项目的人数，补全统计图①即可．
（2）用360°乘以扇形统计图中B的百分比，即可得出答案．
（3）列表可得出所有等可能的结果数以及恰好选中B，E这两项活动的结果数，再利用概率公式可得出答案．
【解答】解：（1）参与此次抽样调查的学生人数是36÷30%＝120（人）．
选择E项目的人数为120﹣30﹣36﹣30﹣6＝18（人），
补全统计图①如图所示．
故答案为：120；
（2）列表如下：
共有20种等可能的结果，其中恰好选中B，E这两项活动的结果有：（B，E），（E，B），共2种，
∴恰好选中B，E这两项活动的概率为．
【点评】本题考查列表法与树状图法，概率公式，条形统计图，扇形统计图，能够读懂统计图，掌握列表法与树状图法、概率公式是解答本题的关键．
21．（9分）如图所示，点O是菱形ABCD对角线的交点，CE∥BD，EB∥AC，连接OE，交BC于F．
（1）求证：四边形OCEB是矩形；
（2）如果设AC＝12，BD＝16，求OE的长．
【答案】见试题解答内容
【分析】（1）先证四边形OBEC为平行四边形，再由菱形的性质可得出∠BOC＝90°，即可得出结论；
（2）根据矩形的性质即可得到OE＝CD＝10．
【解答】（1）证明：∵CE∥BD，EB∥AC，
∴四边形OBEC为平行四边形．
∵四边形ABCD为菱形，
∴AC⊥BD，
∴∠BOC＝90°，
∴四边形OBEC为矩形；
（2）解：∵四边形ABCD是菱形，AC＝12，BD＝16，
∴AC⊥BD，OA＝OC＝AC＝6，OB＝OD＝BD＝8，
∴∠DOC＝90°，CD＝＝＝10，
∵四边形OECD为平行四边形，
∴OE＝CD＝10．
【点评】本题考查了菱形的性质，矩形的判定与性质，平行四边形判定与性质等知识；熟练掌握矩形的判定与性质是解题的关键．
五、解答题（三）：本大题共2小题，第22题13分，第23题14分，满分27分，解答应写出文字说明、证明过程或演算步骤。
22．（13分）解决问题：邓州公安交警部门提醒市民，骑车出行必须严格遵守“一盔一带”的规定．某头盔经销商统计了某品牌头盔7月份到9月份的销量，该品牌头盔7月份销售500个，9月份销售720个，且从7月份到9月份销售量的月增长率相同．
（1）求该品牌头盔销售量的月增长率；
（2）若此种头盔的进价为30元/个，经市场预测，当售价为40元/个时，月销售量为600个，若在此基础上售价每上涨1元/个，则月销售量将减少10个，为使月销售利润达到10000元，而且尽可能让顾客得到实惠，该品牌头盔的实际售价应定为多少元？
【答案】见试题解答内容
【分析】（1）设该品牌头盔销售量的月增长率为x，根据该品牌头盔7月份及9月份的月销售量，即可得出关于x的一元二次方程，解之取其正值即可；
（2）根据月销售利润＝每个头盔的利润×月销售量，即可得出关于y的一元二次方程，解方程即可．
【解答】解：（1）设该品牌头盔销售量的月增长率为x，
依题意，得：500（1+x）2＝720，
解得：x1＝0.2＝20%，x2＝﹣2.2（不合题意，舍去）．
答：该品牌头盔销售量的月增长率为20%．
（2）设该品牌头盔的实际售价为y元，
依题意，得：（y﹣30）[600﹣10（y﹣40）]＝10000，
整理，得：y2﹣130y+4000＝0，
解得：y1＝80（不合题意，舍去），y2＝50，
答：该品牌头盔的实际售价应定为50元．
【点评】本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键．
23．（14分）如图，正方形ABCD中，点E、M、N分别在AB、AD、BC上，DE与MN相交于点O，记∠MOD＝α．
（1）如图1，若∠MOD＝90°，求证：DE＝MN；
（2）如图2，若∠MOD＝45°，边长AB＝4，MN＝，求线段DE的长．
【答案】（1）证明见解答；
（2）线段DE的长是．
【分析】（1）作AG∥MN，交DE于点F，则四边形AGNM是平行四边形，所以AG＝MN，再证明△ADE≌△BAG，得DE＝AG，所以DE＝MN；
（2）作DF∥MN，交BC于点F，则∠EDF＝∠MOD＝45°，推导出AD＝CD＝BC＝AB＝4，DF＝MN＝，则CF＝＝1，求得BF＝3，延长BC于点H，使CH＝AE，连接DH、EF，可证明△CDH≌△ADE，得DH＝DE，∠CDH＝∠ADE，再证明△HDF≌△EDF，得HF＝EF＝AE+1，于是得（4﹣AE）2+32＝（AE+1）2，求得AE＝，则DE＝＝．
【解答】（1）证明：如图1，作AG∥MN，交DE于点F，则∠AFD＝∠MOD＝90°，
∵四边形ABCD是正方形，
∴AM∥GN，DA＝AB，∠DAE＝∠B＝90°，
∴四边形AGNM是平行四边形，∠ADE＝∠BAG＝90°﹣∠DAG，
∴AG＝MN，
在△ADE和△BAG中，
，
∴△ADE≌△BAG（ASA），
∴DE＝AG，
∴DE＝MN．
（2）解：如图2，作DF∥MN，交BC于点F，则∠EDF＝∠MOD＝45°，
∵DM∥FN，
∴四边形DMNF是平行四边形，
∵AB＝4，MN＝，
∴AD＝CD＝BC＝AB＝4，DF＝MN＝，
∵∠DCF＝90°，
∴CF＝＝＝1，
∴BF＝BC﹣CF＝4﹣1＝3，
延长BC于点H，使CH＝AE，连接DH、EF，则∠DCH＝∠A＝∠ADC＝90°，
在△CDH和△ADE中，
，
∴△CDH≌△ADE（SAS），
∴DH＝DE，∠CDH＝∠ADE，
∴∠HDF＝∠CDH+∠CDF＝∠ADE+∠CDF＝∠ADC﹣∠EDF＝90°﹣45°＝45°，
∴∠HDF＝∠EDF，
在△HDF和△EDF中，
，
∴△HDF≌△EDF（SAS），
∴HF＝EF，
∴HF＝CH+CF＝AE+1，
∴EF＝AE+1，
∵BE2+BF2＝EF2，且BE＝4﹣AE，
∴（4﹣AE）2+32＝（AE+1）2，
解得AE＝，
∴DE＝＝＝，
∴线段DE的长是．
【点评】此题重点考查正方形的性质、全等三角形的判定与性质、勾股定理等知识，正确地作出辅助线构造全等三角形是解题的关键．
声明：试题解析著作权属所有，未经书面同意，不得复制发布日期：2024/11/26 1:05:37；用户：18328501451；邮箱：18328501451；学号：43314264A
B
C
D
E
A
﹣
（A，B）
（A，C）
（A，D）
（A，E）
B
（B，A）
﹣
（B，C）
（B，D）
（B，E）
C
（C，A）
（C，B）
﹣
（C，D）
（C，E）
D
（D，A）
（D，B）
（D，C）
﹣
（D，E）
E
（E，A）
（E，B）
（E，C）
（E，D）
﹣