广东省广州市增城区2024-2025学年八年级上学期期中数学试卷

这是一份广东省广州市增城区2024-2025学年八年级上学期期中数学试卷，共28页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．（3分）窗花是中国古老的民间艺术之一，下列窗花作品中为轴对称图形的是（ ）
A．B．
C．D．
2．（3分）下列每组数分别是三根木棒的长度，能用它们摆成三角形的是（ ）
A．3cm，4cm，8cmB．8cm，7cm，15cm
C．5cm，5cm，11cmD．12cm，12cm，20cm
3．（3分）如图，∠AOB是一个任意角，在边OA、OB上分别取OM＝ON，移动角尺，使角尺两边相同的刻度分别与M、N重合，过角尺顶点C的射线OC便是∠AOB的平分线OC，这一做法用到三角形全等的判定方法是（ ）
A．SSSB．SASC．ASAD．HL
4．（3分）如图，△ABC≌△DCB，若AC＝9，BE＝6，则DE的长为（ ）
A．3B．6C．2D．4
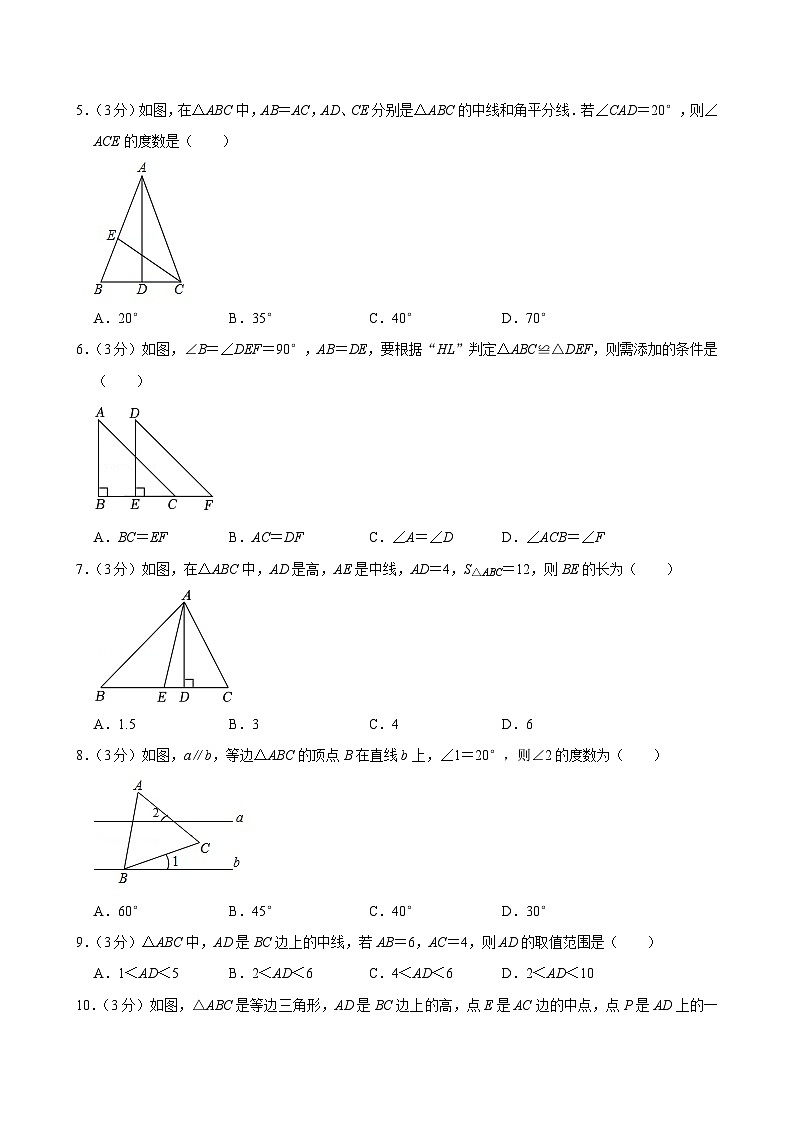
5．（3分）如图，在△ABC中，AB＝AC，AD、CE分别是△ABC的中线和角平分线．若∠CAD＝20°，则∠ACE的度数是（ ）
A．20°B．35°C．40°D．70°
6．（3分）如图，∠B＝∠DEF＝90°，AB＝DE，要根据“HL”判定△ABC≌△DEF，则需添加的条件是（ ）
A．BC＝EFB．AC＝DFC．∠A＝∠DD．∠ACB＝∠F
7．（3分）如图，在△ABC中，AD是高，AE是中线，AD＝4，S△ABC＝12，则BE的长为（ ）
A．1.5B．3C．4D．6
8．（3分）如图，a∥b，等边△ABC的顶点B在直线b上，∠1＝20°，则∠2的度数为（ ）
A．60°B．45°C．40°D．30°
9．（3分）△ABC中，AD是BC边上的中线，若AB＝6，AC＝4，则AD的取值范围是（ ）
A．1＜AD＜5B．2＜AD＜6C．4＜AD＜6D．2＜AD＜10
10．（3分）如图，△ABC是等边三角形，AD是BC边上的高，点E是AC边的中点，点P是AD上的一个动点，当PC+PE最小时，∠CPE的度数是（ ）
A．30°B．45°C．60°D．90°
二、填空题（本题有6个小题，每小题3分，共18分．）
11．（3分）在平面直角坐标系中，点A（3，﹣1）关于y轴对称的点的坐标是 ．
12．（3分）一个多边形的内角和是720°，这个多边形的边数是 ．
13．（3分）一个等腰三角形的两边长为5和8，则此三角形的周长为 ．
14．（3分）如图，在△ABC中，AB＝AC，DE是AB的垂直平分线，若AB＝12，BC＝8，则△BCE的周长为 ．
15．（3分）如图，已知△ABC的周长为15，∠BAC和∠ABC的平分线AD和BE相交于点P．若点P到边AB的距离为2，则△ABC的面积为 ．
16．（3分）在四边形ABCD中，AB＝20cm，BC＝16cm，CD＝24cm，∠B＝∠C，点E为AB的中点．如果点P在线段BC上以4cm/s的速度由B点向C点运动，同时，点Q在线段CD上由C点向D点运动．当点Q的运动速度为 时，能够使△BPE与△CQP全等．
三、解答题（本题有9个小题，共72分，解答要求写出文字说明、证明过程或计算步骤．）
17．（4分）如图，点D是△ABC边BC延长线上一点，∠ACD＝120°，∠B＝20°，求∠A的度数．
18．（4分）如图，AB＝AC，AD＝AE．求证：∠B＝∠C．
19．（6分）如图，在长度为1个单位长度的小正方形组成的正方形网格中，△ABC的三个顶点A，B，C都在格点上．
（1）在图中画出与△ABC关于直线y成轴对称的△A1B1C1；
（2）求△ABC的面积．
20．（6分）如图，点D在AC边上，∠A＝∠B，AE＝BE，∠1＝∠2．
（1）求证：△AEC≌△BED；
（2）若∠1＝45°，求∠BDE的度数．
21．（8分）如图，在Rt△ABC中，∠B＝90°．
（1）尺规作图：在AC边上找一点D，使DB＝DC；（保留作图痕迹，不要求写作法）
（2）在（1）的条件下若BD＝6，求AC的长．
22．（10分）如图1，AP平分∠BAC，PD⊥AB，PE⊥AC，垂足分别为点D、E．
（1）求证：AD＝AE；
（2）在图1的条件下，如图2，点M、N分别在AB、AC上，且PM＝PN，AM＝5，AN＝3，求AD的长．
23．（10分）如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，点D是AB的中点，点E为边AC上一点，连接CD，DE，以DE边在DE的左侧作等边三角形DEF，连接BF．
（1）求证：△BCD为等边三角形；
（2）求证：∠DBF＝∠DCE．
24．（12分）如图，△ABD与△AEC都是等边三角形，连接BE，CD，点M，N分别是BE，CD的中点，连接AM，AN，MN．
（1）求证：BE＝CD；
（2）求证：△AMN是等边三角形；
（3）如图2，△ABD与△AEC都是等腰直角三角形，连接BE，CD，点M，N分别是BE，CD的中点，连接AM，AN．若点N恰好也是AE的中点，且AE＝2，求△ABE的面积．
25．（12分）如图，点A、B分别是x轴、y轴上的两个动点，以B为直角顶点，以AB为腰作等腰Rt△ABC．
（1）如图①，若点C的横坐标为2，点B的坐标为 ；
（2）如图②，过C作CD⊥x轴于点D，连接BD．求∠BDC的大小；
（3）如图③，移动点A，B的位置，使x轴恰好平分∠BAC，BC交x轴于点M，试猜想线段AM、OB、OM之间的数量关系，并说明理由．
2024-2025学年广东省广州市增城区八年级（上）期中数学试卷
参考答案与试题解析
一、选择题（本题有10个小题，每小题3分，满分30分，下面每小题给出的四个选项中只有一个是正确的）
1．（3分）窗花是中国古老的民间艺术之一，下列窗花作品中为轴对称图形的是（ ）
A．B．
C．D．
【答案】A
【分析】如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形．利用轴对称图形的定义进行判断即可．
【解答】解：选项B、C、D中的图形均不能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以不是轴对称图形；
选项A中的图形能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以是轴对称图形；
故选：A．
【点评】本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．
2．（3分）下列每组数分别是三根木棒的长度，能用它们摆成三角形的是（ ）
A．3cm，4cm，8cmB．8cm，7cm，15cm
C．5cm，5cm，11cmD．12cm，12cm，20cm
【答案】D
【分析】根据三角形三边关系定理判断即可．
【解答】解：3+4＜8，A不能摆成三角形；
8+7＝15，B不能摆成三角形；
5+5＜11，C不能摆成三角形；
12+12＞20，20﹣12＜12，D能摆成三角形；
故选：D．
【点评】本题考查的是三角形的三边关系，掌握三角形三边关系定理：三角形两边之和大于第三边、三角形的两边差小于第三边是解题的关键．
3．（3分）如图，∠AOB是一个任意角，在边OA、OB上分别取OM＝ON，移动角尺，使角尺两边相同的刻度分别与M、N重合，过角尺顶点C的射线OC便是∠AOB的平分线OC，这一做法用到三角形全等的判定方法是（ ）
A．SSSB．SASC．ASAD．HL
【答案】A
【分析】根据作图过程可得MO＝NO，MC＝NC，再利用SSS可判定△MCO≌△CNO．
【解答】解：∵在△MCO和△NCO中，
∴△MCO≌△CNO（SSS），
故选：A．
【点评】此题主要考查了基本作图，以及全等三角形的判定，关键是掌握判定三角形全等的方法．
4．（3分）如图，△ABC≌△DCB，若AC＝9，BE＝6，则DE的长为（ ）
A．3B．6C．2D．4
【答案】A
【分析】根据全等三角形的性质及线段的和差求解即可得解．
【解答】解：∵△ABC≌△DCB，AC＝9，
∴BD＝AC＝9，
∵BD＝BE+DE，BE＝6，
∴DE＝3，
故选：A．
【点评】此题考查了全等三角形的性质，熟记“全等三角形的对应边相等”是解题的关键．
5．（3分）如图，在△ABC中，AB＝AC，AD、CE分别是△ABC的中线和角平分线．若∠CAD＝20°，则∠ACE的度数是（ ）
A．20°B．35°C．40°D．70°
【答案】B
【分析】根据等腰三角形的性质得到∠BAD＝∠CAD＝20°，∠ABC＝∠ACB，根据三角形内角和定理求出∠ACB，根据角平分线的定义计算即可．
【解答】解：∵AB＝AC，AD是△ABC的中线，
∴∠BAD＝∠CAD＝20°，∠ABC＝∠ACB，
∴∠ACB＝＝70°，
∵CE是△ABC的角平分线，
∴∠ACE＝∠ACB＝35°，
故选：B．
【点评】本题考查的是等腰三角形的性质，三角形的中线和角平分线以及三角形内角和定理，掌握等腰三角形的三线合一是解题的关键．
6．（3分）如图，∠B＝∠DEF＝90°，AB＝DE，要根据“HL”判定△ABC≌△DEF，则需添加的条件是（ ）
A．BC＝EFB．AC＝DFC．∠A＝∠DD．∠ACB＝∠F
【答案】B
【分析】利用“HL”的判定方法，添加两斜边相等即可．
【解答】解：∵∠B＝∠DEF＝90°，AB＝DE，
∴当添加AC＝DF时，△ABC≌△DEF（HL）．
故选：B．
【点评】本题考查了全等三角形的判定：熟练掌握全等三角形的5种判定方法是解决问题的关键．选用哪一种方法，取决于题目中的已知条件．
7．（3分）如图，在△ABC中，AD是高，AE是中线，AD＝4，S△ABC＝12，则BE的长为（ ）
A．1.5B．3C．4D．6
【答案】B
【分析】利用三角形面积公式求出BC，再根据中线的定义求出BE即可．
【解答】解：∵S△ABC＝BC•AD＝12，AD＝4，
∴BC＝6，
∵AE是中线，
∴BE＝BC＝3．
故选：B．
【点评】本题考查三角形的面积，掌握三角形面积公式及中线的定义是解题的关键．
8．（3分）如图，a∥b，等边△ABC的顶点B在直线b上，∠1＝20°，则∠2的度数为（ ）
A．60°B．45°C．40°D．30°
【答案】C
【分析】过C作CM∥直线l，根据等边三角形性质求出∠ACB＝60°，根据平行线的性质求出∠1＝∠MCB，∠2＝∠ACM，即可求出答案．
【解答】解：∵△ABC是等边三角形，
∴∠ACB＝60°，
过C作CM∥直线l，
∵直线l∥直线m，
∴直线l∥直线m∥CM，
∵∠ACB＝60°，∠1＝20°，
∴∠1＝∠MCB＝20°，
∴∠2＝∠ACM＝∠ACB﹣∠MCB＝60°﹣20°＝40°，
故选：C．
【点评】本题考查了平行线的性质，等边三角形的性质的应用，解此题的关键是能正确作出辅助线，注意：两直线平行，内错角相等．
9．（3分）△ABC中，AD是BC边上的中线，若AB＝6，AC＝4，则AD的取值范围是（ ）
A．1＜AD＜5B．2＜AD＜6C．4＜AD＜6D．2＜AD＜10
【答案】A
【分析】延长AD到E，使AD＝DE，连接BE，证明△ADC≌△EDB（SAS），推出AC＝BE＝4，在△ABE中，根据三角形三边关系定理得出AB﹣BE＜AE＜AB+BE，代入求出即可．
【解答】解：延长AD到E，使AD＝DE，连接BE，
∵AD是BC边上的中线，
∴BD＝CD，
在△ADC和△EDB中，
，
∴△ADC≌△EDB（SAS），
∴AC＝BE＝4，
在△ABE中，AB﹣BE＜AE＜AB+BE，
∴6﹣4＜2AD＜6+4，
∴1＜AD＜5，
故选：A．
【点评】本题考查了全等三角形的性质和判定，三角形的三边关系定理的应用，掌握本题的辅助线的作法是解题的关键．
10．（3分）如图，△ABC是等边三角形，AD是BC边上的高，点E是AC边的中点，点P是AD上的一个动点，当PC+PE最小时，∠CPE的度数是（ ）
A．30°B．45°C．60°D．90°
【答案】C
【分析】连接BE，则BE的长度即为PE与PC和的最小值．再利用等边三角形的性质可得∠PBC＝∠PCB＝30°，即可解决问题；
【解答】解：如连接BE，与AD交于点P，此时PE+PC最小，
∵△ABC是等边三角形，AD⊥BC，
∴PC＝PB，
∴PE+PC＝PB+PE＝BE，
即BE就是PE+PC的最小值，
∵△ABC是等边三角形，
∴∠BCE＝60°，
∵BA＝BC，AE＝EC，
∴BE⊥AC，
∴∠BEC＝90°，
∴∠EBC＝30°，
∵PB＝PC，
∴∠PCB＝∠PBC＝30°，
∴∠CPE＝∠PBC+∠PCB＝60°，
故选：C．
【点评】本题考查的是最短线路问题及等边三角形的性质，熟知两点之间线段最短的知识是解答此题的关键．
二、填空题（本题有6个小题，每小题3分，共18分．）
11．（3分）在平面直角坐标系中，点A（3，﹣1）关于y轴对称的点的坐标是 （﹣3，﹣1） ．
【答案】见试题解答内容
【分析】关于y轴对称的点的横坐标互为相反数，纵坐标相等，由此可得答案．
【解答】解：点A（3，﹣1）关于y轴对称的点的坐标是（﹣3，﹣1）．
故答案为：（﹣3，﹣1）．
【点评】本题考查关于x轴、y轴对称的点的坐标，熟练掌握关于y轴对称的点的坐标特征是解答本题的关键．
12．（3分）一个多边形的内角和是720°，这个多边形的边数是 6 ．
【答案】见试题解答内容
【分析】根据内角和定理180°•（n﹣2）即可求得．
【解答】解：∵多边形的内角和公式为（n﹣2）•180°，
∴（n﹣2）×180°＝720°，
解得n＝6，
∴这个多边形的边数是6．
故答案为：6．
【点评】本题主要考查了多边形的内角和定理即180°•（n﹣2），难度适中．
13．（3分）一个等腰三角形的两边长为5和8，则此三角形的周长为 18或21 ．
【答案】见试题解答内容
【分析】因为已知条件给出的边，哪条边是腰没有明确，所以分两种情况讨论，还要根据三边关系看能否构成三角形．
【解答】解：（1）当5是腰时，5，5，8能够组成三角形，
周长＝5+5+8＝18；
（2）当8是腰时，8，8，5能够组成三角形，
周长＝8+8+5＝21．
因此周长为18或21．
故填18或21．
【点评】本题考查了等腰三角形的性质和三角形的三边关系；已知没有明确腰和底边的题目一定要想到两种情况，分类进行讨论，还应验证各种情况是否能构成三角形进行解答，这点非常重要，也是解题的关键．
14．（3分）如图，在△ABC中，AB＝AC，DE是AB的垂直平分线，若AB＝12，BC＝8，则△BCE的周长为 20 ．
【答案】20．
【分析】证明EA＝EB，EB+EC＝AC，即可解决问题．
【解答】解：∵AB＝AC，AB＝12，
∴AC＝12，
∵DE是AB的垂直平分线，
∴EA＝EB，
∴EB+EC＝EA+EC＝AC；
∴△BCE的周长＝EB+EC+BC＝AC+BC＝12+8＝20；
故答案为：20．
【点评】该题主要考查了线段垂直平分线的性质以及等腰三角形的性质；应牢固掌握等腰三角形、线段垂直平分线等几何知识点的内容，并能灵活运用．
15．（3分）如图，已知△ABC的周长为15，∠BAC和∠ABC的平分线AD和BE相交于点P．若点P到边AB的距离为2，则△ABC的面积为 15 ．
【答案】15．
【分析】连接CP，过点P作PF⊥AB于点F，PH⊥BC于点H，PG⊥AC于点G．可得PG＝PF＝PH＝2．据此即可求解．
【解答】解：如图，连接CP，过点P作PF⊥AB于点F，PH⊥BC于点H，PG⊥AC于点G．
∵AP平分∠CAB，PG⊥AC于点G，PF⊥AB于点F，
∴PG＝PF．
同理可得：PF＝PH．
∴PG＝PF＝PH＝2．
∵△ABC的周长为15，
∴AB+BC+AC＝15．
∴S△ABC＝S△ABP+S△BCP+S△ACP
＝
＝
＝15．
故答案为：15．
【点评】本题考查了角平分线的性质定理：角平分线上的点到角两边的距离相等，熟练掌握该定理是关键．
16．（3分）在四边形ABCD中，AB＝20cm，BC＝16cm，CD＝24cm，∠B＝∠C，点E为AB的中点．如果点P在线段BC上以4cm/s的速度由B点向C点运动，同时，点Q在线段CD上由C点向D点运动．当点Q的运动速度为 4cm/s或5cm/s 时，能够使△BPE与△CQP全等．
【答案】见试题解答内容
【分析】根据线段的中点定义得BE＝10cm，再设点P的运动时间为t s，则BP＝4t cm，从而可得CP＝（16﹣4t）cm，然后根据已知可得分两种情况：当BE＝CP＝10cm，BP＝CQ＝4t cm时；当BE＝CQ＝10cm，BP＝CP＝4t cm时，分别进行计算即可．
【解答】解：∵点E为AB的中点，AB＝20cm，
∴（cm），
设点P的运动时间为t s，则BP＝4t cm，
∵BC＝16cm，
∴CP＝BC﹣BP＝（16﹣4t）cm，
①当BE＝CP＝10cm，BP＝CQ＝4t cm时，△BPE≌△CQP（SAS），
此时16﹣4t＝10，
解得：，
∴CQ＝BP＝16﹣10＝6（cm），
此时点Q的运动速度为：；
②当BE＝CQ＝10cm，BP＝CP＝4t cm时，△BPE≌△CPQ（SAS），
此时4t＝16﹣4t，
解得：t＝2，
此时点Q的运动速度为：10÷2＝5（cm/s）；
综上所述：当点Q的运动速度为4cm/s或5cm/s时，能够使△BPE与△CQP全等．
故答案为：4cm/s或5cm/s．
【点评】本题考查了全等三角形的判定以及分类讨论等知识，熟练掌握全等三角形的判定方法，进行分类讨论是解题的关键．
三、解答题（本题有9个小题，共72分，解答要求写出文字说明、证明过程或计算步骤．）
17．（4分）如图，点D是△ABC边BC延长线上一点，∠ACD＝120°，∠B＝20°，求∠A的度数．
【答案】100°．
【分析】利用三角形的外角性质，可得出∠ACD＝∠B+∠A，再代入∠ACD＝120°，∠B＝20°，即可求出∠A的度数．
【解答】解：∵点D是△ABC边BC延长线上一点，
∴∠ACD＝∠B+∠A，
即120°＝20°+∠A，
∴∠A＝100°．
【点评】本题考查了三角形的外角性质，牢记“三角形的一个外角等于和它不相邻的两个内角的和”是解题的关键．
18．（4分）如图，AB＝AC，AD＝AE．求证：∠B＝∠C．
【答案】见试题解答内容
【分析】要证∠B＝∠C，可利用判定两个三角形全等的方法“两边和它们的夹角对应相等的两个三角形全等”证△ABE≌△ACD，然后由全等三角形对应边相等得出．
【解答】证明：在△ABE与△ACD中，
，
∴△ABE≌△ACD（SAS），
∴∠B＝∠C．
【点评】本题主要考查了两个三角形全等的其中一种判定方法，即“边角边”判定方法．观察出公共角∠A是解决本题的关键．
19．（6分）如图，在长度为1个单位长度的小正方形组成的正方形网格中，△ABC的三个顶点A，B，C都在格点上．
（1）在图中画出与△ABC关于直线y成轴对称的△A1B1C1；
（2）求△ABC的面积．
【答案】（1）图见解答；
（2）．
【分析】（1）依据轴对称的性质，即可得到与△ABC关于直线y成轴对称的△A1B1C1；
（2）依据割补法进行计算，即可得出△ABC的面积．
【解答】解：（1）如图所示，△A1B1C1即为所求；
（2）△ABC的面积＝3×3﹣×2×3﹣×1×2﹣×1×3＝．
【点评】本题主要考查了利用轴对称变换作图，凡是涉及最短距离的问题，一般要考虑线段的性质定理，结合轴对称变换来解决，多数情况要作点关于某直线的对称点．
20．（6分）如图，点D在AC边上，∠A＝∠B，AE＝BE，∠1＝∠2．
（1）求证：△AEC≌△BED；
（2）若∠1＝45°，求∠BDE的度数．
【答案】（1）见解析；
（2）67.5°．
【分析】（1）根据∠2+∠BDE＝∠ADE＝∠1+∠C推出∠C＝∠BDE即可求证；
（2）根据全等三角形的性质可得EC＝ED，∠C＝∠BDE，即可求解．
【解答】（1）证明：∵∠1＝∠2，∠2+∠BDE＝∠ADE＝∠1+∠C，
∴∠BDE＝∠C，
在△AEC和△BED中，
，
∴△AEC≌△BED（AAS），
（2）解：∵△AEC≌△BED，
∴ED＝EC，
∴∠C＝∠EDC，
∵∠1＝45°，
∴，
∴∠BDE＝67.5°．
【点评】本题考查了全等三角形的判定与性质，熟记相关定理内容是解题关键．
21．（8分）如图，在Rt△ABC中，∠B＝90°．
（1）尺规作图：在AC边上找一点D，使DB＝DC；（保留作图痕迹，不要求写作法）
（2）在（1）的条件下若BD＝6，求AC的长．
【答案】（1）见解析；
（2）AC＝12．
【分析】（1）由DB＝DC可得点D在BC的垂直平分线，运用尺规作图——作垂直平分线的方法作出BC的垂直平分线，与AC的交点D即为所求；
（2）由（1）可得CD＝BD＝6，从而∠DBC＝∠C，根据等角的余角相等得到∠ABD＝∠A，从而AD＝BD＝6，根据AC＝AD+CD即可解答．
【解答】解：（1）如图，点D为所求．
（2）由（1）可得CD＝BD＝6，
∴∠DBC＝∠C，
∵∠ABC＝90°，
∴∠ABD+∠CBD＝∠ABC＝90°，
∠A+∠C＝180°﹣∠ABC＝90°，
∴∠ABD＝∠A，
∴AD＝BD＝6，
∴AC＝AD+CD＝6+6＝12．
【点评】本题考查尺规作图——作垂直平分线，等腰三角形的判定及性质，等角的余角相等，解题的关键是掌握相关知识的灵活运用．
22．（10分）如图1，AP平分∠BAC，PD⊥AB，PE⊥AC，垂足分别为点D、E．
（1）求证：AD＝AE；
（2）在图1的条件下，如图2，点M、N分别在AB、AC上，且PM＝PN，AM＝5，AN＝3，求AD的长．
【答案】（1）证明见解答过程；
（2）4．
【分析】（1）根据角平分线性质得到PD＝PE，利用HL证明Rt△APD≌Rt△APE，根据全等三角形的性质即可得解；
（2）利用HL证明Rt△PEN≌Rt△PDM，根据全等三角形的性质得出NE＝MD，根据线段的和差求解即可．
【解答】（1）证明：∵AP平分∠BAC，PD⊥AB，PE⊥AC，
∴PD＝PE，
在Rt△APD和Rt△APE中，
，
∴Rt△APD≌Rt△APE（HL），
∴AD＝AE；
（2）解：在Rt△PEN和Rt△PDM中，
，
∴Rt△PEN≌Rt△PDM（HL），
∴NE＝MD，
∵AM＝AD+MD＝5，AD＝AE＝AN+NE＝AN+MD，
∴AN+MD+MD＝5，
∵AN＝3，
∴MD＝1，
∴AD＝AM﹣MD＝4．
【点评】此题考查了全等三角形的判定与性质、角平分线的性质，熟记全等三角形的判定与性质是解题的关键．
23．（10分）如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，点D是AB的中点，点E为边AC上一点，连接CD，DE，以DE边在DE的左侧作等边三角形DEF，连接BF．
（1）求证：△BCD为等边三角形；
（2）求证：∠DBF＝∠DCE．
【答案】（1）答案见解答过程；
（2）答案见解答过程．
【分析】（1）先求出∠ABC＝60°，再根据直角三角形斜边中线的性质得CD＝BD＝AD，由此可得出结论；
（2）根据等边三角形性质得BD＝CD，DF＝DE，∠BDC＝∠FDE＝60°，由此得∠BDF＝∠CDE，进而可依据“SAS”判定△BDF和△CDE全等，然后根据全等三角形的性质可得出结论．
【解答】证明：（1）在Rt△ABC中，∠ACB＝90°，∠A＝30°，
∴∠ABC＝60°，
∵点D是AB的中点，
∴CD＝BD＝AD＝AB，
∴△BCD为等边三角形；
（2）∵△BCD和△DEF均为等边三角形，
∴BD＝CD，DF＝DE，∠BDC＝∠FDE＝60°，
∴∠BDF+∠FDC＝∠FDC+∠CDE，
∴∠BDF＝∠CDE，
在△BDF和△CDE中，
，
∴△BDF≌△CDE（SAS），
∴∠DBF＝∠DCE．
【点评】此题主要考查了全等三角形的判定与性质，等边三角形的判定与性质，直角三角形斜边上的中线，熟练掌握全等三角形的判定与性质，等边三角形的判定与性质，理解直角三角形斜边上的中线等于斜边的一半是解决问题的关键．
24．（12分）如图，△ABD与△AEC都是等边三角形，连接BE，CD，点M，N分别是BE，CD的中点，连接AM，AN，MN．
（1）求证：BE＝CD；
（2）求证：△AMN是等边三角形；
（3）如图2，△ABD与△AEC都是等腰直角三角形，连接BE，CD，点M，N分别是BE，CD的中点，连接AM，AN．若点N恰好也是AE的中点，且AE＝2，求△ABE的面积．
【答案】（1）见解析；
（2）见解析；
（3）△ABE的面积为2．
【分析】（1）由等边三角形的性质得AB＝AD，AE＝AC，∠BAD＝∠EAC＝60°，可推导出∠BAE＝∠DAC，进而证明△BAE≌△DAC，得BE＝CD；
（2）由BM＝BE，DN＝CD，且BE＝CD，证明BM＝DN，而AB＝AD，∠ABM＝∠ADN，可证明△BAM≌△DAN，得∠BAM＝∠DAN，AM＝AN，可推导出∠MAN＝∠BAD＝60°，则△AMN 是等边三角形；
（3）由等腰直角三角形的性质得AB＝AD，AE＝AC，∠BAD＝∠EAC＝90°，可推导出∠BAE＝∠DAC，进而证明△BAE≌△DAC，得BE＝CD，∠ABE＝∠ADC，而BM＝BE，DN＝CD，所以BM＝DN，可证明△BAM≌△DAN，得∠BAM＝∠DAN，AM＝AN，推导出∠MAN＝∠BAD＝90°，因为AE＝2，点N是AE的中点，所以AM＝AN＝EN＝1，则S△AMN＝AM•AN＝，所以S△AEM＝2S△AMN＝1，S△ABE＝2S△AEM＝2．
【解答】（1）证明：∵△ABD与△AEC 都是等边三角形，
∴AB＝AD，AE＝AC，∠BAD＝∠EAC＝60°，
∴∠BAE＝∠DAC＝60°+∠DAE，
在△BAE和△DAC中，
，
∴△BAE≌△DAC（SAS），
∴BE＝CD；
（2）证明：∵点M，N分别是BE，CD的中点，
∴BM＝BE，DN＝CD，
∵BE＝CD，
∴BM＝DN，
∵△BAE≌△DAC，
∴∠ABE＝∠ADC，
在△BAM和△DAN中，
，
∴△BAM≌△DAN（SAS），
∴∠BAM＝∠DAN，AM＝AN，
∴∠MAN＝∠DAN+∠DAM＝∠BAM+∠DAM＝∠BAD＝60°，
∴△AMN 是等边三角形．
（3）解：∵△ABD与△AEC都是等腰直角三角形，
∴AB＝AD，AE＝AC，∠BAD＝∠EAC＝90°，
∴∠BAE＝∠DAC＝90°+∠DAE，
在△BAE和△DAC中，
，
∴△BAE≌△DAC（SAS），
∴BE＝CD，∠ABE＝∠ADC，
∵点M，N分别是BE，CD的中点，
∴BM＝BE，DN＝CD，
∴BM＝DN，
在△BAM和△DAN中，
，
∴△BAM≌△DAN（SAS），
∴∠BAM＝∠DAN，AM＝AN，
∴∠MAN＝∠DAN+∠DAM＝∠BAM+∠DAM＝∠BAD＝90°，
∵AE＝2，且点N也是AE的中点，
∴AM＝AN＝EN＝AE＝1，
∴S△AMN＝AM•AN＝×1×1＝，
∵AE＝2AN，BE＝2EM，
∴S△AEM＝2S△AMN＝2×＝1，
∴S△ABE＝2S△AEM＝2×1＝2，
∴△ABE的面积为2．
【点评】此题是三角形综合题，重点考查等边三角形的判定与性质、等腰直角三角形的判定与性质、线段中点的定义、全等三角形的判定与性质、三角形的面积公式等知识，此题综合性强，难度较大，证明△BAE≌△DAC是解题的关键．
25．（12分）如图，点A、B分别是x轴、y轴上的两个动点，以B为直角顶点，以AB为腰作等腰Rt△ABC．
（1）如图①，若点C的横坐标为2，点B的坐标为 （0，2） ；
（2）如图②，过C作CD⊥x轴于点D，连接BD．求∠BDC的大小；
（3）如图③，移动点A，B的位置，使x轴恰好平分∠BAC，BC交x轴于点M，试猜想线段AM、OB、OM之间的数量关系，并说明理由．
【答案】（1）（0，2）；
（2）∠BDC＝45°；
（3）AM＝2（OB+OM），理由见解析．
【分析】（1）过点C作y轴垂线CD⊥y轴，证明△DCB≌△AOB（ASA），推出OB＝DC＝2，可得结论；
（2）过C作CE⊥x轴于点E，则CE＝OD，证明Rt△OBD为等腰直角三角形，再求解即可；
（3）OP＝OM，点P在x轴上，AC交y轴于点N，先证明△ABP≌△BCN（ASA），可得AP＝OB+ON，再证明△AOB≌△AON（AAS），可得OB＝ON，再求解即可．
【解答】解：（1）如图①，过点C作y轴垂线CD⊥y轴，即CD＝2（即C点横坐标为2），
∵∠DBC+∠DCB＝90°，
∵∠DBC+∠OBA＝90°，
∴∠DCB＝∠OBA，
∵∠COB＝∠AOB＝90°，
又∵BC＝AB，
∴△DCB≌△AOB（ASA），
∴OB＝DC＝2，
∴B坐标为（0，2）；
（2）∵由①得，CE＝OB，
如图②，过C作CE⊥x轴于点E，则CE＝OD，
∵OB＝OD，
∴Rt△OBD为等腰直角三角形，
∴∠OBD＝∠ODB＝45°，
∴∠BDC＝90°﹣∠ODB＝45°．
（3）∵在Rt△ABM与Rt△BOM中，
作OP＝OM，点P在x轴上，AC交y轴于点N，如图③，
∵∠ABC＝90°，
∴∠OMB+∠OBM＝∠OMB+∠BAM＝90°，
∴∠OBM＝∠BAM，
∵OP＝OM，
∴∠OBM＝∠OBP，
∵AM平分∠BAC，
∴∠BAM＝∠MAC，
∴∠BAC＝∠PBM，
∵△ABC为等腰直角三角形，
∴∠BAC＝∠PBM＝45°，
∴∠ABP＝∠ABC﹣∠PBM＝45°，
∴∠ABP＝∠BCA，
又∵AB＝AC，
∴△ABP≌△BCN（ASA），
∴AP＝BN＝OB+ON，
∵∠BAM＝∠MAC，
∴△AOB≌△AON（AAS），
∴OB＝ON，
∵OP＝OM，
∴AM＝AP+PM＝2（OB+OM）．
【点评】本题属于三角形综合题，考查了坐标与图形，等腰直角三角形的性质，全等三角形的判定和性质等知识，解题的关键是正确寻找全等三角形解决问题，属于中考常考题型．
声明：试题解析著作权属所有，未经书面同意，不得复制发布日期：2024/11/26 1:17:24；用户：18328501451；邮箱：18328501451；学号：43314264